The Ext functor measures extensions of modules and plays a crucial role in homological algebra by classifying how modules can be embedded into one another through exact sequences. Understanding the Ext functor helps you explore relationships between modules beyond mere morphisms, uncovering hidden algebraic structure in categories. Dive deeper into this article to discover how the Ext functor operates and why it is fundamental in advanced mathematics.
Table of Comparison
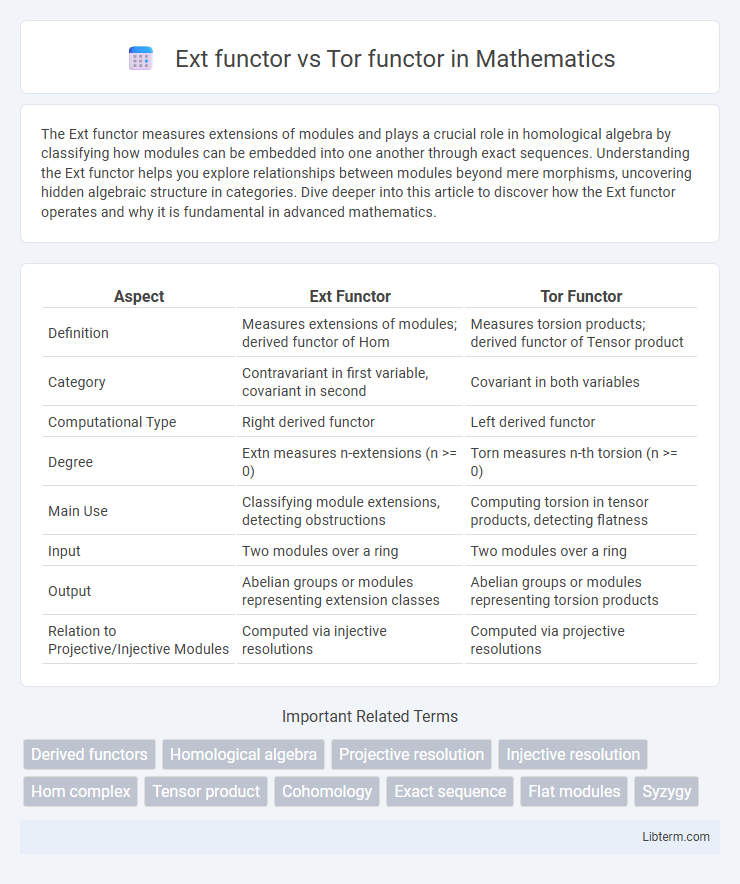
| Aspect | Ext Functor | Tor Functor |
|---|---|---|
| Definition | Measures extensions of modules; derived functor of Hom | Measures torsion products; derived functor of Tensor product |
| Category | Contravariant in first variable, covariant in second | Covariant in both variables |
| Computational Type | Right derived functor | Left derived functor |
| Degree | Extn measures n-extensions (n >= 0) | Torn measures n-th torsion (n >= 0) |
| Main Use | Classifying module extensions, detecting obstructions | Computing torsion in tensor products, detecting flatness |
| Input | Two modules over a ring | Two modules over a ring |
| Output | Abelian groups or modules representing extension classes | Abelian groups or modules representing torsion products |
| Relation to Projective/Injective Modules | Computed via injective resolutions | Computed via projective resolutions |
Introduction to Ext and Tor Functors
Ext functor measures extensions of modules and classifies equivalence classes of module extensions, providing insight into the structure of modules over a ring. Tor functor computes the derived functors of the tensor product, detecting torsion phenomena and measuring how tensoring fails to be exact. Both functors arise from homological algebra and play a critical role in understanding module theory, projective resolutions, and homological dimensions.
Homological Algebra Overview
The Ext functor measures extensions of modules and classifies equivalence classes of module extensions, providing insights into module structure and homological dimensions. The Tor functor, derived from the tensor product, detects torsion phenomena and measures how non-flat a module is by quantifying failure of exactness in tensoring. Both functors arise from projective and injective resolutions, playing central roles in homological algebra for analyzing module relationships and computing derived functors.
Defining the Ext Functor
The Ext functor, defined as Ext^n_R(M, N), measures the extensions of modules M and N over a ring R, capturing equivalence classes of n-step extensions. It arises as the right derived functor of the Hom functor, preserving exactness properties in cohomological contexts. Contrastingly, the Tor functor, Tor_n^R(M, N), emerges as a left derived functor of the tensor product, quantifying torsion phenomena in module tensor products.
Defining the Tor Functor
The Tor functor, denoted as Tor_n^R(-,-), measures the failure of flatness in modules over a ring R by computing the derived functors of the tensor product. Defined through projective resolutions, Tor_n^R(M, N) is the homology at position n of the complex obtained by tensoring a projective resolution of M with the module N. This distinguishes it from the Ext functor, which involves injective resolutions and captures extension classes of modules.
Key Differences Between Ext and Tor
Ext functor measures extensions of modules, capturing how one module can be embedded into another through exact sequences, while Tor functor detects torsion phenomena arising from tensor product operations, reflecting how modules interact under tensoring. Ext is computed via projective or injective resolutions focusing on homomorphisms, whereas Tor uses flat or projective resolutions emphasizing tensor products. The Ext functor generally classifies module extensions and cohomology groups, whereas the Tor functor reveals information about derived tensor products and homological torsion.
Applications of Ext Functor
Ext functor plays a crucial role in homological algebra, particularly in classifying and measuring extensions of modules, making it essential for understanding module structures and cohomological dimensions. It finds significant applications in algebraic topology for computing sheaf cohomology and in representation theory for analyzing extensions between representations. Ext also facilitates the study of derived categories and deformation theory by characterizing obstructions to splitting exact sequences.
Applications of Tor Functor
Tor functor plays a crucial role in homological algebra by measuring the extent to which tensor products fail to be exact, making it indispensable in algebraic topology and module theory. It is used to compute homology groups of chain complexes and analyze extensions and flatness properties of modules over rings. Applications include detecting torsion phenomena in modules, contributing to the study of group cohomology, and facilitating calculations in spectral sequences and sheaf cohomology.
Ext and Tor in Module Theory
Ext and Tor functors are fundamental tools in homological algebra, measuring different aspects of module theory over a ring. Ext functors classify extensions between modules and detect the failure of Hom functor exactness, representing derived functors of Hom, while Tor functors measure the torsion arising from tensor products and represent the derived functors of the tensor product. In module theory, Ext groups provide information about module extensions and cohomology, whereas Tor groups capture information about flatness and projective resolutions, critical for understanding module structure and homological dimensions.
Computational Methods for Ext and Tor
Computational methods for Ext and Tor functors often involve projective or injective resolutions to calculate derived functors in homological algebra. Algorithms such as spectral sequences and Grobner basis techniques enable effective computation of Ext groups and Tor modules in categories like modules over rings or chain complexes. Software packages like Macaulay2 and SageMath implement these methods to handle explicit calculations, improving efficiency in algebraic geometry and representation theory.
Summary: Choosing Between Ext and Tor Functors
Ext functor measures extensions and classifies modules by homological dimension, focusing on right derived functors of Hom, while Tor functor analyzes tensor products and flatness properties as left derived functors of the tensor product. The choice depends on whether the problem involves extensions (use Ext) or tensor product torsion phenomena (use Tor). Both functors reveal complementary aspects of module and homological algebra structures, essential for studying projective resolutions and exact sequences.
Ext functor Infographic
 libterm.com
libterm.com