A null set, also known as an empty set, contains no elements and is represented by the symbol . This concept is fundamental in mathematics, particularly in set theory, where it serves as the identity element for union operations and the baseline for defining subsets. Explore the rest of this article to understand how the null set applies in various mathematical contexts and why Your grasp of this idea matters.
Table of Comparison
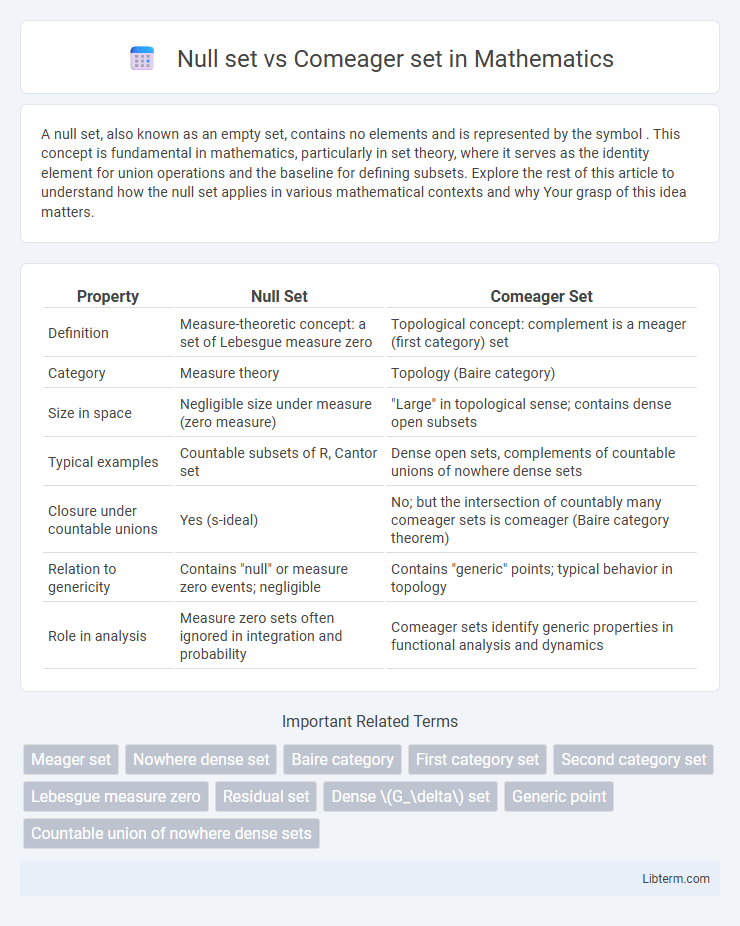
| Property | Null Set | Comeager Set |
|---|---|---|
| Definition | Measure-theoretic concept: a set of Lebesgue measure zero | Topological concept: complement is a meager (first category) set |
| Category | Measure theory | Topology (Baire category) |
| Size in space | Negligible size under measure (zero measure) | "Large" in topological sense; contains dense open subsets |
| Typical examples | Countable subsets of R, Cantor set | Dense open sets, complements of countable unions of nowhere dense sets |
| Closure under countable unions | Yes (s-ideal) | No; but the intersection of countably many comeager sets is comeager (Baire category theorem) |
| Relation to genericity | Contains "null" or measure zero events; negligible | Contains "generic" points; typical behavior in topology |
| Role in analysis | Measure zero sets often ignored in integration and probability | Comeager sets identify generic properties in functional analysis and dynamics |
Introduction to Null Sets and Comeager Sets
Null sets, also known as measure-zero sets, are subsets of a measure space with Lebesgue measure zero, meaning they occupy no volume in the space. Comeager sets, alternatively, are topologically large sets whose complements are meager, or of the first category, in a complete metric space. Both concepts play crucial roles in real analysis and topology, highlighting distinct notions of "smallness" in measure theory and Baire category theory.
Defining the Null Set: Measure-Theoretic Perspective
A null set, in measure theory, is defined as a set with Lebesgue measure zero, indicating its negligible size within a given space. These sets can be covered by countably many intervals whose total length sums to an arbitrarily small positive number. Null sets contrast with comeager sets, which are dense in a topological sense and related to category rather than measure.
Understanding Comeager Sets: Baire Category Theory
Comeager sets, also known as residual sets, are complements of meager (or null) sets in Baire category theory, and they are dense in complete metric spaces. Unlike null sets, which have Lebesgue measure zero, comeager sets contain a countable intersection of open dense sets, making them topologically large despite possibly having measure zero. These sets play a crucial role in functional analysis and topology by identifying "generic" conditions where typical properties hold.
Key Properties of Null Sets
Null sets, defined as sets of Lebesgue measure zero, have the key property that they can be covered by countably many intervals with arbitrarily small total length, making them negligible in measure theory. These sets are closed under countable unions, meaning the union of countably many null sets remains null, and any subset of a null set is also null. Unlike comeager sets, which are large in the sense of category and contain dense open sets, null sets are small in a measure-theoretic sense, highlighting a fundamental difference in size notions between measure and category.
Essential Characteristics of Comeager Sets
Comeager sets, also known as residual sets, are characterized by their construction as countable intersections of dense open sets in a complete metric space, reflecting their topological largeness. Unlike null sets, which have Lebesgue measure zero and are negligible in measure theory, comeager sets are significant in the category sense as they are 'large' or typical with respect to Baire category. Essential characteristics of comeager sets include their density, robustness under countable intersections, and prevalence in Polish spaces where they often represent generic properties.
Null Sets vs. Comeager Sets: Fundamental Differences
Null sets consist of points in a measure space with zero measure, representing negligible size in terms of Lebesgue measure, while comeager sets are defined topologically as countable intersections of dense open sets within a complete metric space, indicating generic properties. Null sets are measure-theoretic concepts highlighting "smallness" in size, whereas comeager sets capture "largeness" or typicality from a Baire category perspective. The fundamental difference lies in their frameworks: null sets rely on measure theory and emphasize measure zero, while comeager sets depend on topological density and category, often reflecting complementary notions of "almost everywhere" versus "typical" elements.
Examples Illustrating Null Sets and Comeager Sets
A null set, such as the Cantor set within the interval [0,1], has Lebesgue measure zero but contains uncountably many points, making it "small" in measure theory yet "large" in cardinality. Conversely, a comeager set like the set of irrational numbers in the real line is dense and contains a countable intersection of open dense sets, reflecting "largeness" in category theory despite being measure-full. These examples illustrate how null sets are negligible in measure but can be topologically significant, while comeager sets are topologically large but may have zero measure.
Applications in Analysis and Topology
Null sets, defined by having measure zero, are crucial in measure theory and integration, enabling the exclusion of negligible subsets without affecting integral values. Comeager sets, characterized by the Baire category theorem as countable intersections of dense open sets, play a key role in topology and functional analysis by identifying "large" subsets in complete metric spaces. These concepts facilitate the study of generic properties, where null sets highlight measure-theoretic exceptions and comeager sets ensure typical behavior in spaces of functions or sequences.
Importance in Real Analysis and Descriptive Set Theory
The distinction between null sets and comeager sets is fundamental in real analysis and descriptive set theory, as null sets represent subsets of real numbers with Lebesgue measure zero, while comeager sets form dense, co-meager subsets characterized by category rather than measure. Null sets help identify properties that hold "almost everywhere," essential for integration and measure-theoretic arguments, whereas comeager sets reveal topological genericity, crucial for understanding typical behavior in Baire spaces. This dual viewpoint enables mathematicians to analyze functions and sets from both measure and category perspectives, enriching the study of continuity, differentiability, and complexity in Polish spaces.
Conclusion: Distinguishing Null and Comeager Sets
Null sets are measure-theoretic concepts representing subsets of a given space with Lebesgue measure zero, indicating they are "small" in terms of volume or probability. Comeager sets belong to category theory in topology, defined as complements of meager (first category) sets, signifying they are "large" in terms of Baire category and contain a dense G-delta set. The primary distinction lies in their foundational frameworks: null sets emphasize measure and size, while comeager sets highlight topological density and typicality, making them fundamentally different notions of "largeness" in analysis.
Null set Infographic
 libterm.com
libterm.com