Tensor algebra provides a powerful framework for manipulating multi-dimensional arrays, extending linear algebra concepts to higher dimensions. It plays a crucial role in physics, engineering, and computer graphics by enabling complex transformations and modeling of multidimensional data. Discover how tensor algebra can enhance your understanding of advanced mathematical structures by reading the rest of this article.
Table of Comparison
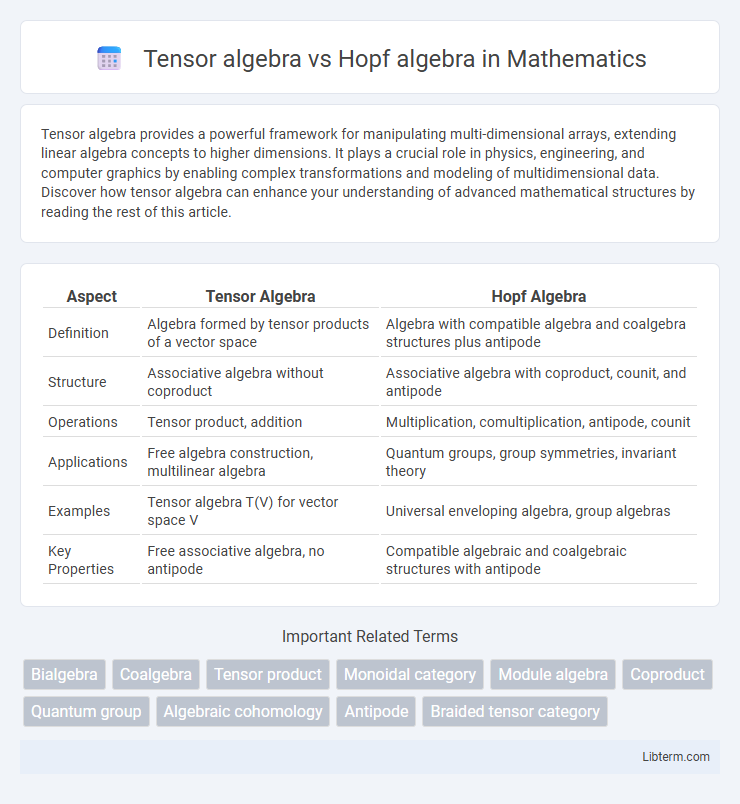
| Aspect | Tensor Algebra | Hopf Algebra |
|---|---|---|
| Definition | Algebra formed by tensor products of a vector space | Algebra with compatible algebra and coalgebra structures plus antipode |
| Structure | Associative algebra without coproduct | Associative algebra with coproduct, counit, and antipode |
| Operations | Tensor product, addition | Multiplication, comultiplication, antipode, counit |
| Applications | Free algebra construction, multilinear algebra | Quantum groups, group symmetries, invariant theory |
| Examples | Tensor algebra T(V) for vector space V | Universal enveloping algebra, group algebras |
| Key Properties | Free associative algebra, no antipode | Compatible algebraic and coalgebraic structures with antipode |
Introduction to Tensor Algebra and Hopf Algebra
Tensor algebra is an algebraic structure that generalizes vectors and linear transformations by enabling the construction of higher-order tensors through tensor products, forming a graded algebra over a vector space. Hopf algebra extends this framework by integrating compatible algebraic and coalgebraic structures, including antipode maps, which provide an abstraction of group symmetries in a categorical context. Understanding tensor algebra lays the foundation for grasping Hopf algebras, as the latter enriches tensor algebra concepts with additional operations critical for quantum groups and non-commutative geometry.
Fundamental Concepts: Tensors vs Algebras
Tensor algebra constructs a graded algebra from a vector space by forming tensor products of vectors, enabling the representation of multilinear maps and complex geometric structures. Hopf algebra extends algebraic structures by combining operations like multiplication, comultiplication, antipode, unit, and counit, introducing a rich framework crucial for studying symmetry, quantum groups, and algebraic topology. The fundamental difference lies in tensor algebra focusing on linear and multilinear tensor constructions, while Hopf algebra encapsulates both algebraic and coalgebraic properties, enabling duality and advanced algebraic operations.
Basic Operations in Tensor Algebra
Tensor algebra primarily involves operations such as tensor product, tensor addition, and scalar multiplication, which combine to form an algebraic structure over a vector space. The tensor product operation allows the construction of higher-order tensors from lower-order ones, enabling multilinear mappings and representations in various dimensions. In contrast, Hopf algebras extend tensor algebra by incorporating additional structures like comultiplication, counit, and antipode, facilitating dualities and symmetries crucial in quantum groups and algebraic topology.
Core Structures of Hopf Algebra
Hopf algebras extend tensor algebras by incorporating additional core structures such as a coproduct, counit, and antipode, which collectively define a compatible coalgebra and algebra framework. The coproduct allows Hopf algebras to model duality and symmetry operations, enabling the decomposition of elements into tensor products within the algebra. These fundamental structures make Hopf algebras central in fields like quantum groups and algebraic topology, where tensor algebras alone lack the necessary dual and inversion properties.
Key Differences Between Tensor and Hopf Algebras
Tensor algebras provide a free associative algebra constructed from a vector space, emphasizing multilinear operations and concatenation of tensors, while Hopf algebras integrate algebraic structures with coalgebra features, including antipodes, enabling duality and symmetry in algebraic operations. The key difference lies in Hopf algebras possessing a coproduct, counit, and antipode, facilitating the study of group-like and quantum group structures, whereas tensor algebras lack these coalgebraic properties. Tensor algebras serve as foundational objects for building multilinear maps, whereas Hopf algebras are central in fields like algebraic topology, quantum groups, and noncommutative geometry due to their richer structure.
Applications in Mathematics and Physics
Tensor algebra provides a foundational framework for multilinear algebra and is extensively used in differential geometry, representation theory, and quantum mechanics to describe vector spaces and their tensor products. Hopf algebra, combining algebraic structures such as algebras, coalgebras, and antipodes, plays a crucial role in quantum groups, noncommutative geometry, and the study of symmetries in mathematical physics. Both algebras are instrumental in formulating invariants in topology and understanding symmetry operations in particle physics, with Hopf algebra offering enhanced structural insights beyond the capabilities of tensor algebra.
Representation Theory: Tensor vs Hopf Algebras
Tensor algebra serves as a foundational structure in representation theory by enabling the construction of free algebras generated by vector spaces, facilitating the study of linear representations through multilinear maps. Hopf algebras extend this framework by incorporating coproducts, counits, and antipodes, allowing for duality and symmetry operations critical in quantum group theory and noncommutative geometry. The representation theory of Hopf algebras captures both algebraic and coalgebraic actions, providing a richer and more versatile context compared to tensor algebras, particularly in categorifying symmetry and implementing braided monoidal categories.
Examples and Illustrations
Tensor algebra, constructed from a vector space by forming all possible tensor products, exemplifies a free associative algebra, commonly used in multilinear algebra and representation theory. Hopf algebra extends this structure by incorporating compatible algebraic operations such as coproduct, counit, and antipode, enabling duality and symmetry analysis, with prominent examples including group algebras and quantum groups. Illustrations often contrast the pure algebraic product in tensor algebras with the richer structure in Hopf algebras that supports operations like convolution, crucial in topology, quantum field theory, and algebraic geometry.
Computational Aspects and Challenges
Tensor algebra provides a framework for multilinear computations through the manipulation of tensor products and linear maps, facilitating efficient representation of data structures in machine learning and physics. Hopf algebras introduce additional algebraic structures like antipodes and coproducts, enabling more complex symmetries and dualities but increasing computational complexity when implementing algebraic operations and cohomological calculations. Challenges in Hopf algebra computations arise from handling intricate coalgebra structures and ensuring consistency in antipode calculations, which require advanced algorithms and symbolic computation tools beyond standard tensor algebra methods.
Future Directions and Research Trends
Research on tensor algebra is evolving towards applications in machine learning and quantum computing due to its ability to handle multidimensional data efficiently. Hopf algebra's future directions emphasize advancements in quantum group theory and noncommutative geometry, providing tools for symmetry analysis in physics. Emerging trends explore the interplay between tensor and Hopf algebras to develop new algebraic frameworks for solving complex problems in theoretical physics and computer science.
Tensor algebra Infographic
 libterm.com
libterm.com