Mastering geometry sharpens your spatial reasoning and problem-solving skills, essential in various fields from architecture to engineering. Understanding shapes, angles, and theorems enables you to analyze and interpret visual information more effectively. Explore the rest of this article to enhance your grasp of geometric principles and their real-world applications.
Table of Comparison
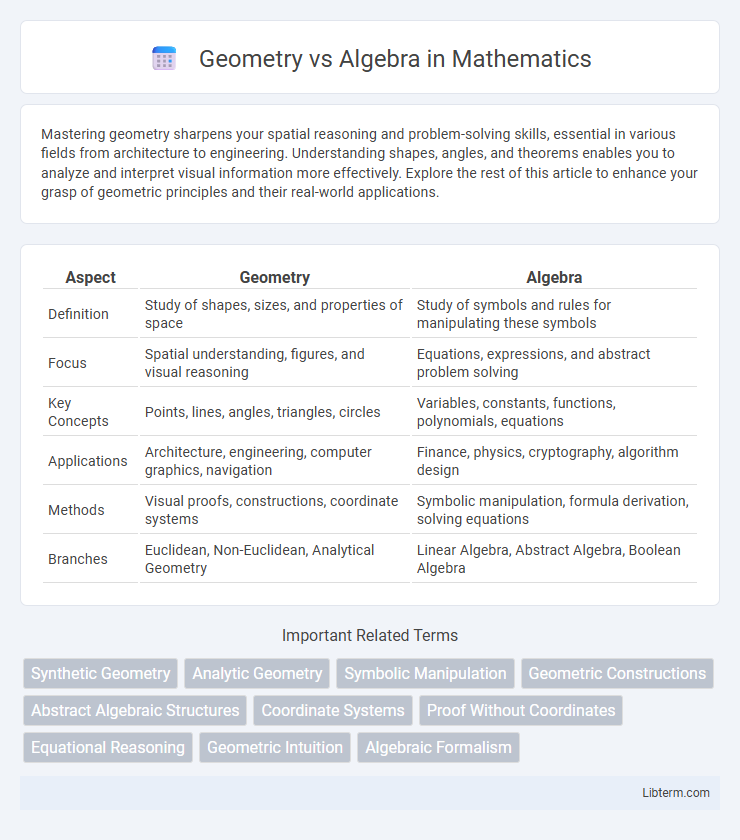
| Aspect | Geometry | Algebra |
|---|---|---|
| Definition | Study of shapes, sizes, and properties of space | Study of symbols and rules for manipulating these symbols |
| Focus | Spatial understanding, figures, and visual reasoning | Equations, expressions, and abstract problem solving |
| Key Concepts | Points, lines, angles, triangles, circles | Variables, constants, functions, polynomials, equations |
| Applications | Architecture, engineering, computer graphics, navigation | Finance, physics, cryptography, algorithm design |
| Methods | Visual proofs, constructions, coordinate systems | Symbolic manipulation, formula derivation, solving equations |
| Branches | Euclidean, Non-Euclidean, Analytical Geometry | Linear Algebra, Abstract Algebra, Boolean Algebra |
Introduction to Geometry and Algebra
Geometry studies shapes, sizes, and the properties of space using points, lines, angles, and surfaces, emphasizing visual reasoning and spatial understanding. Algebra involves manipulating symbols and solving equations to represent and analyze relationships between quantities, focusing on abstract mathematical structures and operations. Both branches serve as foundational components of mathematics, enabling problem-solving across various scientific and engineering fields.
Defining Geometry: Shapes, Space, and Properties
Geometry explores the properties and relationships of shapes, spaces, and their dimensions, emphasizing points, lines, planes, angles, and figures such as polygons and circles. It studies spatial reasoning and measurement, including concepts like area, volume, congruence, and similarity, which are essential in real-world applications. Unlike algebra's focus on abstract symbols and equations, geometry visually represents mathematical concepts to analyze and understand the physical world.
Understanding Algebra: Symbols and Equations
Algebra involves the manipulation of symbols and the solving of equations to represent and analyze relationships numerically. Understanding algebra requires recognizing variables, constants, and coefficients within expressions and applying operations to isolate unknowns. Mastery of these concepts enables the translation of real-world problems into solvable mathematical models.
Historical Development of Geometry and Algebra
The historical development of geometry dates back to ancient civilizations such as the Egyptians and Babylonians, who used geometric principles for land measurement and construction, with Euclid's "Elements" laying the foundational axioms and theorems. Algebra originated in the Islamic Golden Age through scholars like Al-Khwarizmi, whose works formalized solving equations and introduced systematic methods, evolving into symbolic algebra during the Renaissance with European mathematicians like Viete. The parallel evolution of geometry and algebra culminated in analytic geometry, pioneered by Rene Descartes, which unified spatial and abstract mathematical concepts.
Key Differences Between Geometry and Algebra
Geometry studies shapes, sizes, and spatial relationships through points, lines, surfaces, and solids, emphasizing visual and spatial reasoning. Algebra focuses on generalizing arithmetic operations using symbols and variables to solve equations and understand abstract patterns. While geometry deals with spatial intuition and measurement, algebra centers on symbolic manipulation and formulaic problem-solving.
Applications of Geometry in Real Life
Geometry plays a crucial role in various real-life applications such as architecture, engineering, and computer graphics, where understanding shapes, sizes, and spatial relationships is essential. The principles of geometry are used to design buildings, create virtual simulations, and develop navigation systems based on coordinate geometry and measurements. Practical uses also include manufacturing processes, robotics, and even art, making geometry indispensable in solving everyday problems involving space and structure.
Practical Uses of Algebra in Everyday Situations
Algebra simplifies problem-solving by representing real-world situations with variables and equations, enabling efficient budgeting, cooking adjustments, and time management. It plays a critical role in calculating interest rates, loan repayments, and financial forecasting to support informed economic decisions. Mastery of algebraic principles enhances logical reasoning and empowers practical tasks such as converting units or determining proportions in daily activities.
How Geometry and Algebra Interact
Geometry and algebra interact through the use of coordinate systems, enabling geometric shapes to be expressed as algebraic equations and graphed on a plane. Algebraic methods solve geometric problems by manipulating equations representing lines, curves, and surfaces, facilitating precise measurement and relationship analysis. The synergy between these fields underpins analytic geometry, allowing the translation of spatial problems into algebraic forms and vice versa.
Learning Challenges in Geometry vs Algebra
Learning challenges in geometry often stem from spatial reasoning difficulties and the need to visualize shapes, angles, and dimensions, whereas algebra challenges typically arise from abstract symbol manipulation and understanding variable relationships. Students may struggle with applying geometric theorems and proofs due to the requirement of logical deduction and spatial intuition, while algebra learners face hurdles in mastering equation solving and function comprehension. Developing strong problem-solving strategies and conceptual understanding is essential in overcoming these distinct difficulties in geometry and algebra education.
Choosing Between Geometry and Algebra in Education
Choosing between geometry and algebra in education depends on a student's learning goals and strengths. Geometry enhances spatial reasoning and visualization skills through the study of shapes, angles, and theorems, while algebra focuses on abstract thinking and problem-solving using variables and equations. Incorporating both subjects provides a comprehensive mathematical foundation essential for STEM careers and higher-level mathematics.
Geometry Infographic
 libterm.com
libterm.com