A closed set in mathematics is a set that contains all its limit points, meaning it includes its own boundary within a given topological space. Understanding closed sets is crucial for grasping concepts in analysis and topology, as they play a key role in defining continuity, convergence, and compactness. Explore the rest of this article to deepen your understanding of closed sets and their applications in various mathematical contexts.
Table of Comparison
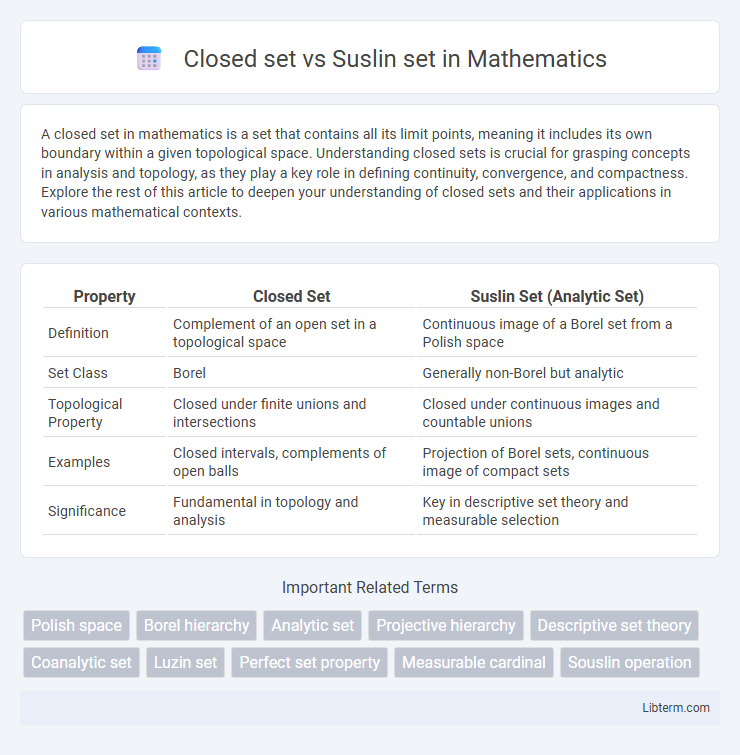
| Property | Closed Set | Suslin Set (Analytic Set) |
|---|---|---|
| Definition | Complement of an open set in a topological space | Continuous image of a Borel set from a Polish space |
| Set Class | Borel | Generally non-Borel but analytic |
| Topological Property | Closed under finite unions and intersections | Closed under continuous images and countable unions |
| Examples | Closed intervals, complements of open balls | Projection of Borel sets, continuous image of compact sets |
| Significance | Fundamental in topology and analysis | Key in descriptive set theory and measurable selection |
Introduction to Closed Sets and Suslin Sets
A closed set in topology is defined as a set containing all its limit points, making it the complement of an open set in a given topological space. Suslin sets, also known as analytic sets, extend beyond Borel sets and are formed through continuous images of Polish spaces, playing a crucial role in descriptive set theory. Understanding closed sets provides foundational knowledge, while Suslin sets introduce a complex hierarchy important for advanced measure theory and real analysis.
Definitions: What Are Closed Sets?
Closed sets are defined as subsets of a topological space that contain all their limit points, meaning the set equals its closure. In contrast, Suslin sets, also called analytic sets, arise in descriptive set theory as continuous images of Polish spaces and may not be closed but are still measurable and have well-defined structure. Understanding closed sets is fundamental for grasping more complex constructs like Suslin sets, as closed sets are the simplest example of Borel sets used extensively in topology and measure theory.
Definitions: What Are Suslin Sets?
Suslin sets, also known as analytic sets, are subsets of Polish spaces that can be obtained as continuous images of Borel sets and represent a broader class than closed sets, which are defined as sets containing all their limit points. Unlike closed sets, Suslin sets need not be closed or open but retain key measurability properties essential in descriptive set theory. The distinction lies in Suslin sets potentially being more complex, involving projections of Borel sets, while closed sets are strictly defined via topological closure.
Key Differences Between Closed Sets and Suslin Sets
Closed sets are defined as sets containing all their limit points within a topological space, typically characterized by their stability under limit operations and complement openness. Suslin sets, or analytic sets, extend beyond Borel sets and are obtained through continuous images of Polish spaces, often not necessarily closed or Borel. The key difference lies in closed sets being topologically well-behaved and fully characterized by closure properties, whereas Suslin sets embody a broader, more complex class with potentially intricate descriptive set-theoretic structures.
Hierarchical Relationships in Descriptive Set Theory
Closed sets form the foundational level in the Borel hierarchy, representing the simplest class of definable sets within descriptive set theory. Suslin sets, also known as analytic sets, extend beyond Borel sets by being continuous images of Borel sets and occupy a higher complexity level in the projective hierarchy. The hierarchical relationship places closed sets strictly inside the class of Suslin sets, reflecting the progression from topologically simpler to more complex definability properties.
Examples of Closed Sets in Mathematics
Closed sets in mathematics include examples such as the interval [0, 1] on the real number line, the set of all points on a circle in Euclidean space, and the complement of any open set. Suslin sets, also known as analytic sets, extend beyond closed sets by including continuous images of Borel sets, yet closed sets remain foundational in topology and analysis due to their property of containing all their limit points. Classic closed sets appear in metric spaces, where every convergent sequence within the set has its limit also contained in the set, exemplified by the set of integers within the real numbers.
Examples of Suslin Sets and Their Properties
Suslin sets, also known as analytic sets, include all closed sets and can be constructed using continuous images of Borel sets, such as the projection of closed subsets of Polish spaces. For example, the projection of the closed set {(x,y) in R2 | xy = 1} onto the x-axis forms a Suslin set that is not necessarily closed or Borel. Suslin sets are universally measurable, have the property of Baire, and are stable under continuous image and countable unions, distinguishing them from strictly closed sets.
Applications of Closed Sets and Suslin Sets
Closed sets are fundamental in topology and analysis, commonly used in convergence theorems, compactness criteria, and boundary definitions critical for solving partial differential equations and optimization problems. Suslin sets, also known as analytic sets, play a pivotal role in descriptive set theory and measure theory, especially in characterizing projective sets and aiding in the study of measurability and classification problems in Polish spaces. Applications of Suslin sets extend to functional analysis and probability theory, where they help analyze complex structures beyond Borel sets.
Closed Sets vs Suslin Sets: Importance in Topology
Closed sets are fundamental in topology, defined as complements of open sets and crucial for understanding continuity and convergence. Suslin sets, also known as analytic sets, extend beyond Borel sets and play a significant role in descriptive set theory by capturing complex definability properties in Polish spaces. The distinction between closed and Suslin sets highlights the hierarchy of set complexity, impacting measurable selection theorems and the study of definable sets in advanced topological analysis.
Conclusion: Comparing Closed and Suslin Sets
Closed sets are well-defined and stable under topological operations, making them fundamental in classical topology, while Suslin sets, as analytic sets, extend beyond Borel sets and capture more complex structures in descriptive set theory. Suslin sets are universally measurable and have strong regularity properties, which closed sets inherently possess, but Suslin sets allow greater flexibility in handling projective hierarchies. Comparing both highlights that closed sets serve as building blocks of topology, whereas Suslin sets enable advanced analysis in measurable and definability contexts.
Closed set Infographic
 libterm.com
libterm.com