Simple design focuses on clean lines, minimal colors, and decluttered spaces to create a calming and efficient environment. Emphasizing functionality and clarity helps you achieve an aesthetic that is both modern and timeless. Explore the rest of the article to discover practical tips for incorporating simplicity into your daily life.
Table of Comparison
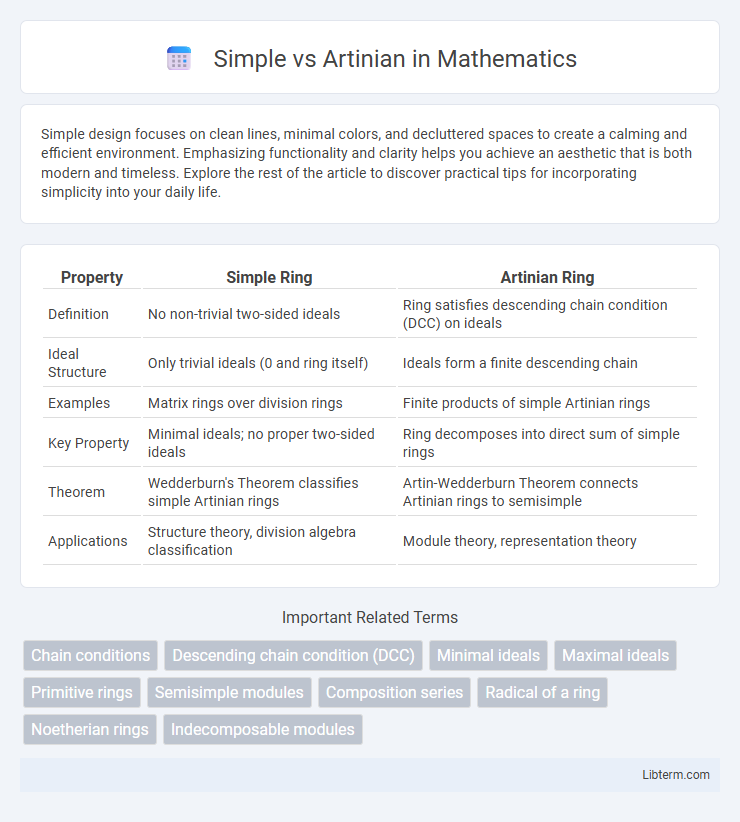
| Property | Simple Ring | Artinian Ring |
|---|---|---|
| Definition | No non-trivial two-sided ideals | Ring satisfies descending chain condition (DCC) on ideals |
| Ideal Structure | Only trivial ideals (0 and ring itself) | Ideals form a finite descending chain |
| Examples | Matrix rings over division rings | Finite products of simple Artinian rings |
| Key Property | Minimal ideals; no proper two-sided ideals | Ring decomposes into direct sum of simple rings |
| Theorem | Wedderburn's Theorem classifies simple Artinian rings | Artin-Wedderburn Theorem connects Artinian rings to semisimple |
| Applications | Structure theory, division algebra classification | Module theory, representation theory |
Understanding Simple and Artinian Rings
Simple rings are algebraic structures with no nontrivial two-sided ideals, making them indivisible in terms of ideal decomposition. Artinian rings satisfy the descending chain condition on ideals, ensuring that any decreasing sequence of ideals eventually stabilizes and these rings are characterized by their finiteness properties. Understanding the difference involves recognizing that all simple rings are prime and often Artinian, but not all Artinian rings are simple, highlighting the complexity in ring classification and structure theory.
Definitions: What is a Simple Ring?
A simple ring is a nonzero ring with no two-sided ideals other than the zero ideal and the ring itself, indicating a minimal ideal structure. This property ensures the ring cannot be decomposed into smaller, nontrivial two-sided ideals, making it a foundational concept in ring theory. Simple rings often appear in the study of matrix rings over division rings and play a crucial role in the classification of algebraic structures.
Defining Artinian Rings
Artinian rings are characterized by the descending chain condition on ideals, meaning every descending sequence of ideals eventually stabilizes. Simple rings, in contrast, have no nontrivial two-sided ideals, often serving as building blocks in ring theory. The defining property of Artinian rings ensures they possess a finite composition length, distinguishing them from simple rings that may lack this finiteness condition.
Key Properties of Simple Rings
Simple rings are characterized by having no nontrivial two-sided ideals and a nonzero identity element, which ensures irreducibility in their module structure. Artinian rings satisfy the descending chain condition on ideals, guaranteeing finite dimensionality over their center and decomposability into simple components. The key property of simple rings is that every module is semisimple and they are isomorphic to matrix rings over division rings, forming building blocks in the Artin-Wedderburn theorem.
Key Properties of Artinian Rings
Artinian rings are characterized by the descending chain condition on ideals, ensuring every descending sequence of ideals stabilizes. Unlike simple rings, which have no nontrivial two-sided ideals, Artinian rings may have a more intricate ideal structure but always have finite length as modules over themselves. Key properties include the decomposition into a finite direct product of simple Artinian rings and the finite-dimensionality of these rings over a division ring.
Comparing Simple and Artinian Structures
Simple structures are algebraic systems containing no nontrivial proper ideals, making them irreducible and straightforward in composition. Artinian structures satisfy the descending chain condition on ideals, ensuring they decompose into a finite direct sum of simple modules or components. Comparing these, simple structures emphasize minimality and indivisibility, while Artinian structures highlight finiteness conditions that guarantee decomposability into simpler parts.
Examples of Simple vs Artinian Rings
Simple rings include matrix rings like M_n(F), where F is a field, with no nontrivial two-sided ideals. Artinian rings encompass all simple Artinian rings such as M_n(F), but also include semisimple rings like direct products of matrix rings over division rings, which satisfy the descending chain condition on ideals. For instance, a division ring D is both simple and Artinian, while a finite product of division rings forms an Artinian ring that is not simple.
Simple Modules Versus Artinian Modules
Simple modules are modules with no proper nonzero submodules, representing the building blocks of module theory. Artinian modules satisfy the descending chain condition on submodules, ensuring every decreasing sequence of submodules stabilizes after finitely many steps. While all simple modules are Artinian due to their minimal structure, Artinian modules may contain proper submodules and are not necessarily simple.
Applications in Abstract Algebra
Simple rings serve as the building blocks in ring theory, characterized by having no nontrivial two-sided ideals, enabling classification of irreducible modules and structure analysis. Artinian rings, defined by the descending chain condition on ideals, facilitate decomposition theorems like the Artin-Wedderburn theorem, which classifies semisimple rings into matrix rings over division rings. These concepts are crucial in module theory, representation theory, and homological algebra, aiding in the understanding of algebraic structures and their morphisms.
Summary: Distinguishing Simple and Artinian
Simple rings are algebraic structures with no nontrivial two-sided ideals, ensuring indivisibility, while Artinian rings satisfy the descending chain condition on ideals, guaranteeing a finite structure. Every simple Artinian ring is isomorphic to a matrix ring over a division ring, providing a complete classification via the Artin-Wedderburn theorem. The key distinction lies in simplicity focusing on ideal structure absence, whereas Artinian property emphasizes finiteness and decomposition properties of the ring.
Simple Infographic
 libterm.com
libterm.com