Countable nouns refer to objects, people, or concepts that can be quantified individually, such as books, apples, or cars. They have both singular and plural forms and are used with numbers and articles like "a" or "an" in the singular form. Explore the rest of the article to master the rules and examples of countable nouns in English.
Table of Comparison
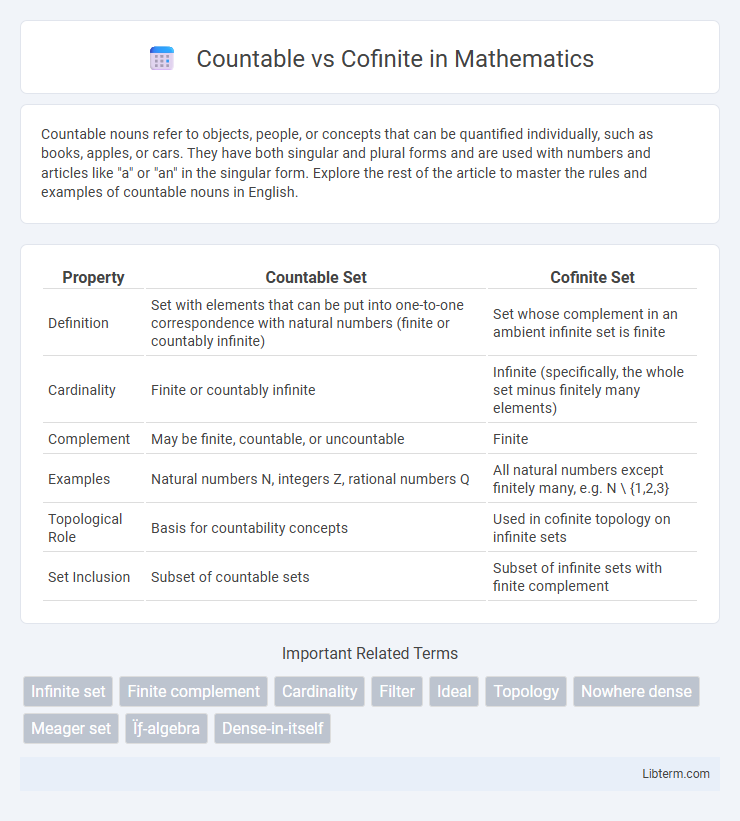
| Property | Countable Set | Cofinite Set |
|---|---|---|
| Definition | Set with elements that can be put into one-to-one correspondence with natural numbers (finite or countably infinite) | Set whose complement in an ambient infinite set is finite |
| Cardinality | Finite or countably infinite | Infinite (specifically, the whole set minus finitely many elements) |
| Complement | May be finite, countable, or uncountable | Finite |
| Examples | Natural numbers N, integers Z, rational numbers Q | All natural numbers except finitely many, e.g. N \ {1,2,3} |
| Topological Role | Basis for countability concepts | Used in cofinite topology on infinite sets |
| Set Inclusion | Subset of countable sets | Subset of infinite sets with finite complement |
Introduction to Countable and Cofinite Sets
Countable sets are those with elements that can be put into a one-to-one correspondence with natural numbers, allowing enumeration of their members. Cofinite sets are subsets of a given infinite set where the complement is finite, meaning all but finitely many elements belong to the set. Understanding countable versus cofinite sets is essential in set theory, topology, and analysis for characterizing infinite structures and their properties.
Definitions: Countable Sets
Countable sets are defined as sets with elements that can be put into one-to-one correspondence with the natural numbers, meaning they are either finite or countably infinite. Examples include the set of integers, rational numbers, and any finite set. Countability is a fundamental concept in set theory, distinguishing sets with manageable cardinality from uncountable sets such as the real numbers.
Definitions: Cofinite Sets
Cofinite sets are subsets of a given universal set whose complements are finite, meaning the set contains all elements except for a finite number of them. In set theory, a cofinite set within an infinite universe is significant because it retains "almost all" elements, differing only by a limited amount. This property contrasts with countable sets, which are finite or countably infinite, whereas cofinite sets are characterized by their large size relative to their finite complement.
Key Differences Between Countable and Cofinite
Countable sets are defined by their ability to be listed in a sequence, either finite or equivalent to the natural numbers, meaning they can be put into one-to-one correspondence with N. Cofinite sets are subsets of an infinite set where their complements are finite, making the majority of the infinite set included except for a finite number of elements. The key difference lies in countability referring to the cardinality and enumerability of a set, whereas cofinite specifically relates to the nature of the set's complement within an infinite universal set.
Examples of Countable Sets
Examples of countable sets include the set of all natural numbers, integers, and rational numbers, each of which can be put into a one-to-one correspondence with the natural numbers. The set of prime numbers and the set of all finite-length strings over a finite alphabet are also countable because they can be enumerated. Countable sets are characterized by their ability to be listed in a sequence, contrasting with uncountable sets like the real numbers.
Examples of Cofinite Sets
Cofinite sets are subsets of a set whose complements are finite, such as the set of all natural numbers excluding a small finite subset like {1, 2, 3}. For example, in the set of integers Z, the set Z \ {-1, 0, 1} is cofinite because its complement {-1, 0, 1} is finite. Cofinite sets frequently arise in topology and algebra, particularly when defining cofinite topologies where open sets have finite complements.
Countable vs Cofinite in Set Theory
In set theory, a countable set is one whose elements can be put into a one-to-one correspondence with the natural numbers, indicating that the set is either finite or countably infinite. A cofinite set is the complement of a finite set within a given universal set, meaning it contains all elements except for a finite number of exceptions. Countable sets can be infinite, whereas cofinite sets are characterized by having a finite complement, making cofinite sets uncountably large if the universal set is infinite.
Properties and Applications
Countable sets have a one-to-one correspondence with the natural numbers, making their size either finite or countably infinite, while cofinite sets have complements that are finite, meaning only a limited number of elements are excluded from the universal set. Properties of countable sets include closure under subsets, countable unions, and Cartesian products, whereas cofinite sets form a filter on infinite sets and are closed under finite intersections and supersets. Applications of countable sets appear in enumerations, algorithm design, and discrete mathematics, while cofinite sets are crucial in topology for defining cofinite topologies and in algebra for dealing with ideals and convergence criteria.
Countable and Cofinite in Topology
Countable sets in topology are those with elements that can be put into a one-to-one correspondence with the natural numbers, often used to describe discrete or separable spaces. Cofinite topology on a set is defined by declaring the open sets to be either the entire set or any subset whose complement is finite, which makes the space T1 and compact but not necessarily Hausdorff. The interplay between countable sets and cofinite topology highlights discrete versus dense properties, as cofinite topology enforces finiteness on complements while countability constraints the size of sets.
Summary and Conclusion
Countable sets have elements that can be listed in a one-to-one correspondence with natural numbers, while cofinite sets are those whose complements in a larger set are finite. The distinction highlights that countability concerns the size of the set itself, whereas cofiniteness focuses on the finiteness of its complement. Understanding the relationship between these concepts is crucial in topology and set theory for analyzing infinite structures and their properties.
Countable Infographic
 libterm.com
libterm.com