Complex geometry explores shapes and spaces defined by complex numbers, revealing intricate structures unobservable in real-number geometry. This field combines algebraic and differential methods to investigate complex manifolds and varieties, offering deep insights into both theoretical and applied mathematics. Discover how complex geometry can transform your understanding of multidimensional spaces by reading the rest of the article.
Table of Comparison
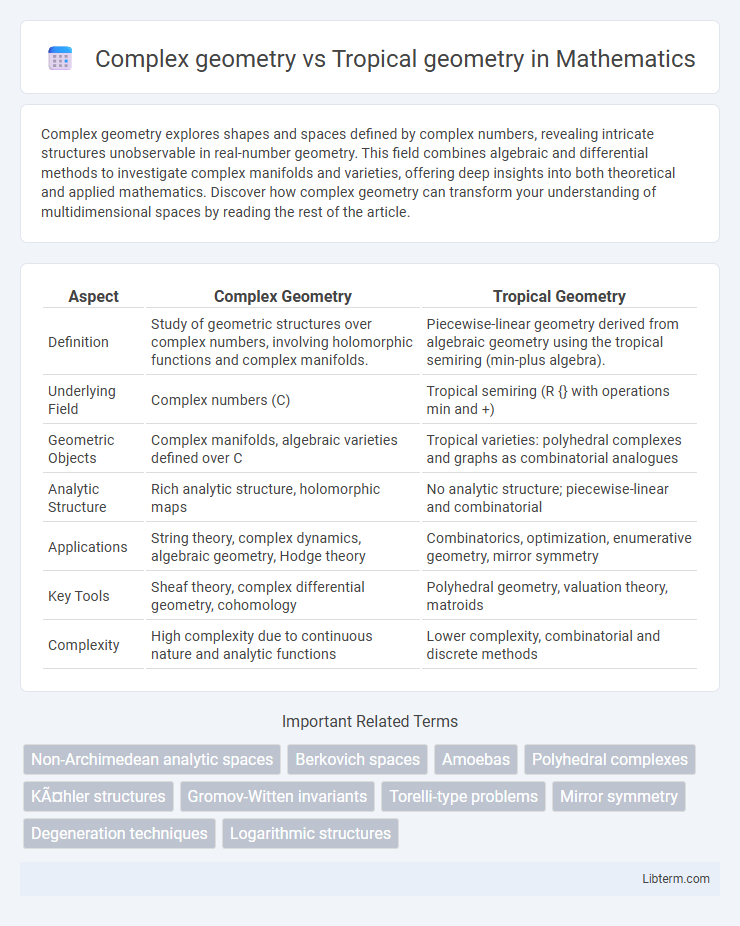
| Aspect | Complex Geometry | Tropical Geometry |
|---|---|---|
| Definition | Study of geometric structures over complex numbers, involving holomorphic functions and complex manifolds. | Piecewise-linear geometry derived from algebraic geometry using the tropical semiring (min-plus algebra). |
| Underlying Field | Complex numbers (C) | Tropical semiring (R {} with operations min and +) |
| Geometric Objects | Complex manifolds, algebraic varieties defined over C | Tropical varieties: polyhedral complexes and graphs as combinatorial analogues |
| Analytic Structure | Rich analytic structure, holomorphic maps | No analytic structure; piecewise-linear and combinatorial |
| Applications | String theory, complex dynamics, algebraic geometry, Hodge theory | Combinatorics, optimization, enumerative geometry, mirror symmetry |
| Key Tools | Sheaf theory, complex differential geometry, cohomology | Polyhedral geometry, valuation theory, matroids |
| Complexity | High complexity due to continuous nature and analytic functions | Lower complexity, combinatorial and discrete methods |
Introduction to Complex Geometry
Complex geometry studies shapes defined by complex numbers and holomorphic functions, emphasizing complex manifolds, complex algebraic varieties, and their rich structures such as Kahler metrics and Hodge theory. It explores properties arising from the complex structure, including complex dimension and analyticity, which differ fundamentally from real geometry. These foundational concepts contrast with tropical geometry, which simplifies algebraic varieties using piecewise-linear structures in tropical semirings.
Foundations of Tropical Geometry
Foundations of Tropical Geometry establish a combinatorial framework that replaces classical algebraic operations with tropical addition and multiplication, transforming polynomial equations into piecewise-linear structures. While Complex Geometry studies solutions over the complex numbers with smooth, continuous shapes, Tropical Geometry interprets these solutions as polyhedral complexes, offering a simplified yet powerful tool for analyzing algebraic varieties through their tropicalizations. Tropicalization maps classical algebraic curves to combinatorial graphs, revealing intricate correspondences and facilitating computations in enumerative geometry and moduli spaces.
Historical Development of Both Fields
Complex geometry, rooted in the 19th century through the works of Bernhard Riemann and later Henri Poincare, developed as a rigorous study of complex manifolds and algebraic varieties using tools from differential geometry and complex analysis. Tropical geometry emerged in the late 20th century as a combinatorial shadow of algebraic geometry, formalized through the work of Grigory Mikhalkin and Bernd Sturmfels, translating classical problems into piecewise-linear structures over the tropical semiring. While complex geometry evolved from classical geometric and analytic foundations, tropical geometry arose from advances in combinatorics, polyhedral geometry, and the desire to simplify complex algebraic varieties into discrete, computationally accessible models.
Key Concepts and Tools: Complex vs Tropical
Complex geometry utilizes complex manifolds and holomorphic functions to study shapes and spaces with intricate structures governed by complex numbers, emphasizing tools like sheaf theory and Hodge theory. Tropical geometry, a piecewise-linear counterpart, replaces classical operations with tropical addition and multiplication, focusing on combinatorial structures such as polyhedral complexes and valuations. Key distinctions include complex geometry's reliance on analytic continuation and complex differential forms versus tropical geometry's use of min-plus algebra and tropical varieties to simplify and approximate algebraic varieties.
Intersection Theory Comparison
Intersection theory in complex geometry relies on classical algebraic tools to compute intersection numbers of subvarieties within complex projective spaces, utilizing cohomology and homology theories to understand their geometric properties. Tropical geometry reformulates intersection theory via combinatorial and piecewise-linear structures, representing tropical varieties as polyhedral complexes whose intersections correspond to stable tropical intersection numbers governed by balancing conditions. Compared to complex geometry, tropical intersection theory offers computational advantages by translating algebraic problems into discrete combinatorial ones, enabling explicit calculation of intersection multiplicities through lattice point counts and Newton polytope subdivisions.
Varieties and Spaces: Complex vs Tropical Structures
Complex geometry studies varieties defined over the complex numbers, where spaces exhibit rich structures derived from complex manifolds and holomorphic functions, enabling powerful tools like sheaf theory and Hodge decomposition. Tropical geometry, in contrast, analyzes tropical varieties shaped by piecewise-linear objects over the tropical semiring, transforming algebraic varieties into combinatorial polyhedral complexes that capture essential geometric and topological features in a simplified, discrete framework. These tropical structures serve as skeletons of complex varieties, providing a bridge between continuous complex spaces and discrete combinatorial models in algebraic geometry.
Applications in Algebraic Geometry
Complex geometry explores algebraic varieties over the field of complex numbers, providing rich tools for analyzing smooth structures, holomorphic functions, and characteristic classes. Tropical geometry translates complex algebraic problems into combinatorial and piecewise-linear settings, enabling simpler calculations of intersection theory and moduli spaces. Applications in algebraic geometry benefit from tropical methods by offering computationally efficient approaches to study degenerations, curve counting, and mirror symmetry phenomena.
Connections to Mirror Symmetry
Complex geometry and tropical geometry both contribute crucial insights to mirror symmetry by offering complementary frameworks for understanding Calabi-Yau manifolds. Complex geometry studies these manifolds through holomorphic structures and moduli spaces, while tropical geometry provides piecewise-linear analogs that simplify computations and reveal combinatorial structures. The interplay between these geometries enables deeper exploration of mirror pairs, facilitating the calculation of Gromov-Witten invariants and illuminating the intricate correspondence predicted by mirror symmetry.
Current Research and Open Problems
Current research in complex geometry emphasizes the study of Calabi-Yau manifolds and their moduli spaces, exploring mirror symmetry and Hodge theory to understand deep connections between algebraic and differential geometry. Tropical geometry, a piecewise-linear shadow of algebraic geometry, focuses on combinatorial structures and has advanced applications in enumerative geometry, non-archimedean analytic spaces, and optimization problems. Open problems include extending tropical methods to higher-dimensional varieties, understanding tropical analogues of complex geometric invariants, and developing a unified framework linking complex and tropical geometries through degeneration techniques.
Future Directions in Complex and Tropical Geometry
Future directions in complex and tropical geometry emphasize deepening the interplay between their combinatorial and analytic aspects, aiming to develop new invariants that capture subtle geometric properties across both fields. Advances in mirror symmetry and non-Archimedean geometry are expected to catalyze breakthroughs in understanding degeneration patterns and moduli spaces. Computational approaches leveraging tropical techniques will increasingly facilitate explicit calculations and classification problems in complex geometry.
Complex geometry Infographic
 libterm.com
libterm.com