Following a strict order ensures tasks are completed efficiently and deadlines are met without confusion or delay. It minimizes errors by providing clear guidance on each step, enabling smoother workflows and better resource management. Explore the rest of the article to discover practical strategies for implementing strict order in your projects.
Table of Comparison
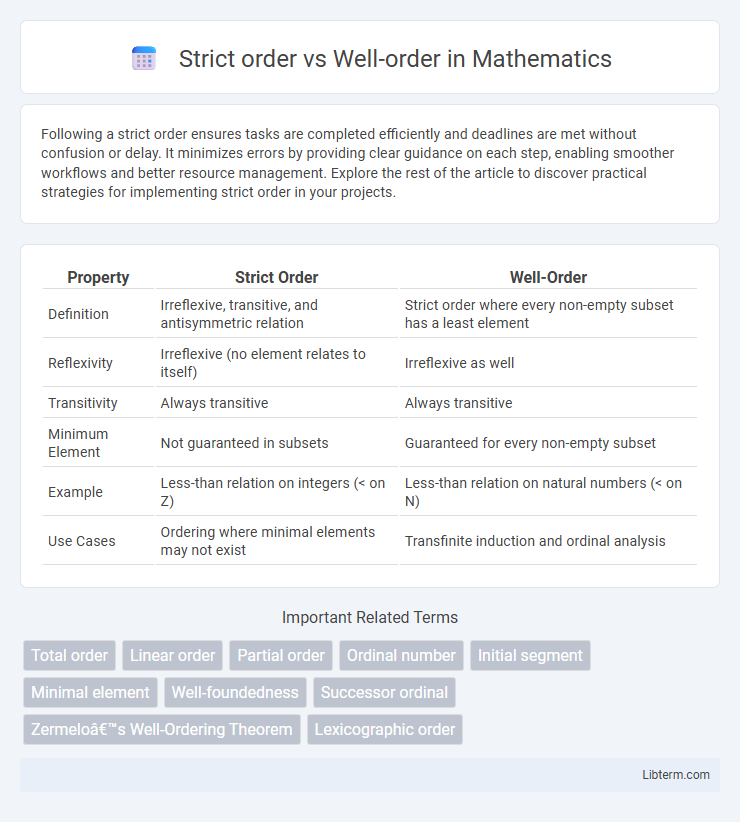
| Property | Strict Order | Well-Order |
|---|---|---|
| Definition | Irreflexive, transitive, and antisymmetric relation | Strict order where every non-empty subset has a least element |
| Reflexivity | Irreflexive (no element relates to itself) | Irreflexive as well |
| Transitivity | Always transitive | Always transitive |
| Minimum Element | Not guaranteed in subsets | Guaranteed for every non-empty subset |
| Example | Less-than relation on integers (< on Z) | Less-than relation on natural numbers (< on N) |
| Use Cases | Ordering where minimal elements may not exist | Transfinite induction and ordinal analysis |
Introduction to Order Relations
Order relations define how elements within a set are compared and arranged, with strict orders being irreflexive and transitive, ensuring no element relates to itself and maintaining a consistent direction in comparisons. Well-orders extend strict orders by requiring every non-empty subset to have a least element, enabling comprehensive induction principles crucial in set theory and mathematical proofs. Understanding these distinctions is fundamental for examining ordered structures and their applications in logic and topology.
Defining Strict Order
Strict order is a binary relation that is irreflexive and transitive, meaning no element is related to itself and the relation preserves order through chains of elements. It differs from well-order by not requiring every non-empty subset to have a least element, which is essential for well-orders. Strict orders are foundational in order theory, facilitating the study of ordered sets without the minimal element condition.
Understanding Well-Order
A well-order is a strict order with the added property that every non-empty subset has a least element, ensuring no infinite descending chains exist. This characteristic distinguishes well-orders from general strict orders, enabling transfinite induction and ordinal analysis. Understanding well-ordering is crucial in set theory and foundations of mathematics, where it underpins proofs involving ordinals and hierarchical structures.
Key Properties of Strict Orders
Strict orders are binary relations characterized by irreflexivity and transitivity, ensuring no element is related to itself and if an element a is related to b and b to c, then a is related to c. Unlike well-orders, strict orders do not require every non-empty subset to have a least element, meaning well-orders are strict orders with the added property of well-foundedness. Key properties of strict orders include antisymmetry and the lack of cycles, establishing a foundation for comparison without necessarily guaranteeing minimal elements in subsets.
Essential Characteristics of Well-Orders
A well-order is a strict total order in which every non-empty subset has a least element, ensuring no infinite descending chains exist. This essential characteristic distinguishes well-orders from general strict orders that may lack minimal elements in some subsets. Well-orders enable transfinite induction and recursion, playing a critical role in set theory and ordinal analysis.
Comparison: Strict Order vs Well-Order
Strict order is a binary relation that is irreflexive and transitive, defining a hierarchy where elements can be compared without allowing equality or cycles. Well-order extends strict order by requiring every non-empty subset to have a least element, ensuring no infinite descending chains exist. This fundamental difference enables well-orders to support transfinite induction and ordinal analysis, unlike general strict orders.
Examples of Strict Orders
Strict orders are binary relations that are irreflexive, transitive, and antisymmetric, exemplified by the "less than" relation (<) on real numbers, where no element is related to itself and if a < b and b < c, then a < c. Another example is the "strict subset" relation () on sets, which orders subsets without including equality, ensuring proper hierarchical arrangement. These orders differ from well-orders as strict orders need not have a least element in every non-empty subset, contrasting with the well-ordering principle exemplified by the natural numbers with usual ordering.
Examples of Well-Orders
A well-order is a type of strict order where every non-empty subset has a least element, such as the set of natural numbers (N) with the usual "less than" (<) relation. Another example is any ordinal number, like o + 1, which extends the natural numbers by adding an element greater than all natural numbers, maintaining a well-ordering. In contrast, strict orders like the usual order on real numbers do not qualify as well-orders because there are subsets, such as the open interval (0,1), that lack a least element.
Applications in Set Theory and Mathematics
Strict orders, defined by irreflexivity and transitivity, are essential in ranking elements without ties, which is vital in set theory for comparing elements in partially ordered sets. Well-orders extend this concept by ensuring every non-empty subset has a least element, enabling transfinite induction and ordinal number theory. These properties underpin critical mathematical constructions such as ordinal analysis, proof theory, and foundational aspects of the hierarchy of infinite sets.
Summary and Key Takeaways
Strict order is a binary relation that is transitive and irreflexive, meaning no element relates to itself and the order is consistent without loops. Well-order extends strict order by requiring every non-empty subset to have a least element, ensuring a minimum exists for any subset. The key distinction lies in well-order enabling ordinal analysis and transfinite induction, essential for advanced mathematical proofs and set theory.
Strict order Infographic
 libterm.com
libterm.com