Schur decomposition is a powerful matrix factorization technique that expresses any square matrix as a unitary matrix multiplied by an upper triangular matrix. This method simplifies eigenvalue computation and is widely used in numerical linear algebra and system stability analysis. Explore the rest of the article to understand how Schur decomposition can enhance your matrix computations.
Table of Comparison
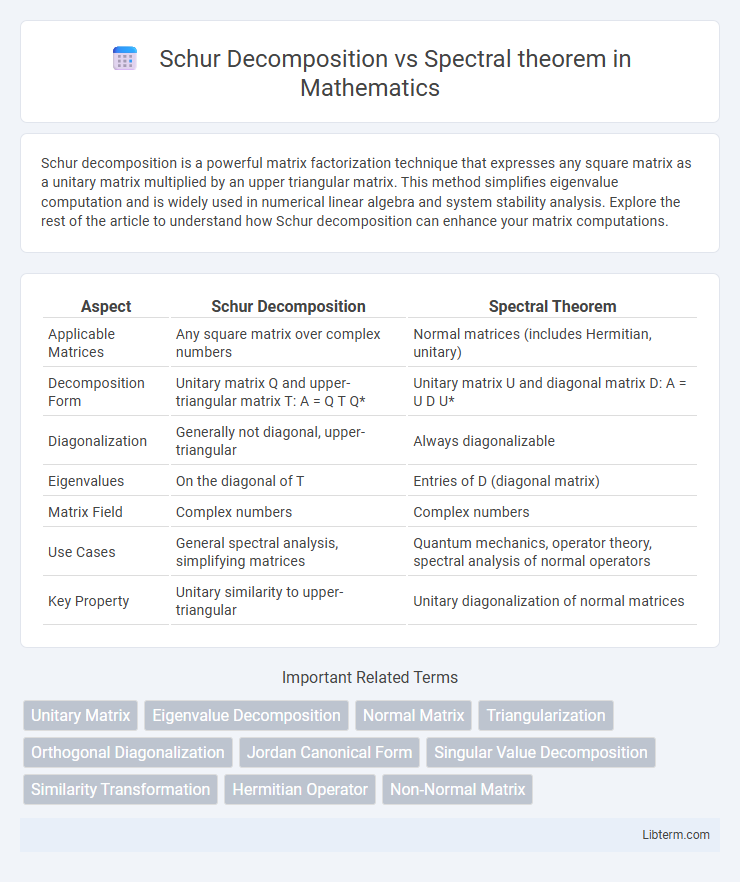
| Aspect | Schur Decomposition | Spectral Theorem |
|---|---|---|
| Applicable Matrices | Any square matrix over complex numbers | Normal matrices (includes Hermitian, unitary) |
| Decomposition Form | Unitary matrix Q and upper-triangular matrix T: A = Q T Q* | Unitary matrix U and diagonal matrix D: A = U D U* |
| Diagonalization | Generally not diagonal, upper-triangular | Always diagonalizable |
| Eigenvalues | On the diagonal of T | Entries of D (diagonal matrix) |
| Matrix Field | Complex numbers | Complex numbers |
| Use Cases | General spectral analysis, simplifying matrices | Quantum mechanics, operator theory, spectral analysis of normal operators |
| Key Property | Unitary similarity to upper-triangular | Unitary diagonalization of normal matrices |
Introduction to Schur Decomposition and the Spectral Theorem
Schur Decomposition represents any square matrix as a product of a unitary matrix and an upper triangular matrix, providing a critical tool for analyzing non-normal operators. The Spectral Theorem specifically applies to normal matrices, guaranteeing their diagonalization through a unitary transformation with eigenvalues on the diagonal. Both concepts underpin linear algebraic spectral analysis but differ in their scope: Schur Decomposition is more general, while the Spectral Theorem offers stronger structural insights for normal matrices.
Mathematical Foundations of Schur Decomposition
Schur Decomposition expresses any square matrix \( A \) as \( A = QUQ^* \), where \( Q \) is a unitary matrix and \( U \) is an upper triangular matrix with eigenvalues of \( A \) on its diagonal, emphasizing orthonormality and similarity transformations in complex vector spaces. The decomposition relies on the existence of an orthonormal basis of generalized eigenvectors and the fundamental fact that every square matrix can be unitarily triangularized, reflecting the matrix's spectral properties in a triangular form. Unlike the Spectral Theorem, which requires matrix normality for diagonalization, Schur Decomposition applies to all square matrices, offering a more general framework for analyzing matrix spectra and structure in linear algebra.
Spectral Theorem: Key Concepts and Definitions
The Spectral Theorem characterizes normal operators on finite-dimensional inner product spaces by stating they can be diagonalized via an orthonormal basis of eigenvectors, linking each eigenvector to a corresponding eigenvalue that forms the operator's spectrum. This theorem guarantees the existence of a unitary matrix \(U\) such that \(U^*AU\) is diagonal, highlighting the importance of normality and unitary diagonalizability in spectral analysis. In contrast, Schur Decomposition provides an upper-triangular matrix similar to the original operator but does not necessarily yield diagonal matrices unless the operator is normal, emphasizing the Spectral Theorem's stronger structural implications for Hermitian and normal matrices.
Conditions for Applicability of Each Theorem
Schur Decomposition applies to all square matrices over the complex numbers, requiring no special conditions beyond the matrix being complex and square, allowing any matrix to be decomposed into a unitary matrix and an upper triangular matrix. The Spectral Theorem requires the matrix to be normal (i.e., commute with its conjugate transpose) and applies to both real symmetric and complex normal matrices, ensuring diagonalizability via a unitary or orthogonal transformation. While Schur Decomposition guarantees triangularization for any complex square matrix, the Spectral Theorem's applicability is restricted, providing full diagonalization only under the normality condition.
Geometric Interpretation: Schur vs Spectral
Schur decomposition represents any square matrix as a unitary matrix and an upper triangular matrix, providing a geometric interpretation where the original linear transformation is expressed through an orthonormal basis but without diagonalization. The spectral theorem applies specifically to normal matrices, allowing diagonalization via a unitary matrix, which geometrically corresponds to rotating the space to align with eigenvectors, revealing pure scaling along orthogonal directions. Schur's approach ensures a triangular form for all matrices, highlighting invariant subspaces, while the spectral theorem's geometric clarity emerges from orthogonal eigenbasis and real-valued eigenvalues in symmetric cases.
Eigenvalues and Eigenvectors: Comparative Analysis
Schur Decomposition expresses any square matrix as a unitary matrix multiplied by an upper triangular matrix, revealing eigenvalues on the diagonal without explicitly providing eigenvectors, whereas the Spectral Theorem applies to normal matrices guaranteeing diagonalization via an orthonormal basis of eigenvectors. Eigenvalues obtained from Schur Decomposition correspond to the diagonal elements of the triangular matrix, whereas the Spectral Theorem ensures real eigenvalues for Hermitian matrices and orthogonal eigenvectors. This comparative analysis highlights that Schur Decomposition is more general for eigenvalue extraction but lacks explicit eigenvector information compared to the Spectral Theorem's comprehensive eigenstructure characterization in normal matrices.
Matrix Types: Normal, Hermitian, and Others
Schur Decomposition applies to any square matrix, representing it as a unitary matrix times an upper triangular matrix, while the Spectral Theorem specifically applies to normal matrices, including Hermitian matrices, enabling diagonalization via a unitary transformation. Hermitian matrices are a subset of normal matrices characterized by real eigenvalues and orthonormal eigenvectors, directly diagonalizable using the Spectral Theorem. Non-normal matrices, which do not satisfy the commutation relation with their adjoint, cannot be diagonalized by the Spectral Theorem but still admit a Schur Decomposition, making it a more general tool in linear algebra.
Computational Aspects and Efficiency
Schur Decomposition provides a numerically stable method for decomposing any square matrix into a unitary matrix and an upper triangular matrix, making it highly efficient for computational tasks involving eigenvalues and invariant subspaces. The Spectral Theorem applies specifically to normal matrices, offering a decomposition into a unitary matrix and a diagonal matrix which simplifies eigenvalue computation but is limited in scope. Schur Decomposition's broader applicability and compatibility with iterative algorithms enhance its efficiency in practical computations compared to the Spectral Theorem.
Practical Applications in Science and Engineering
Schur decomposition enables efficient numerical solutions for non-Hermitian matrices in control system design and stability analysis, while the spectral theorem provides orthogonal diagonalization crucial for quantum mechanics and vibration analysis involving Hermitian operators. Engineers leverage Schur decomposition for real-time signal processing and system identification, whereas the spectral theorem facilitates modal analysis in mechanical structures and electronic circuit simulation. Both decompositions optimize computational algorithms in scientific computing, enhancing the accuracy of eigenvalue problems essential to physics and engineering disciplines.
Summary Table: Schur Decomposition vs Spectral Theorem
Schur Decomposition applies to any square matrix, producing a unitary matrix and an upper triangular matrix, while the Spectral Theorem requires a normal matrix and results in a unitary matrix and a diagonal matrix. The eigenvalues appear on the diagonal in both decompositions; however, the Schur form is generally upper triangular, not necessarily diagonal. In numerical linear algebra, Schur Decomposition is more broadly applicable, whereas the Spectral Theorem provides diagonalization with orthogonal eigenvectors for symmetric or normal matrices.
Schur Decomposition Infographic
 libterm.com
libterm.com