Unital algebra is an algebraic structure equipped with a multiplicative identity element, often denoted as 1, which satisfies the property that multiplying any element by this identity leaves the element unchanged. This concept plays a crucial role in various branches of mathematics, including ring theory and linear algebra, where the presence of a unit element ensures the stability of operations and simplifies computations. Explore the rest of the article to deepen your understanding of unital algebras and their applications.
Table of Comparison
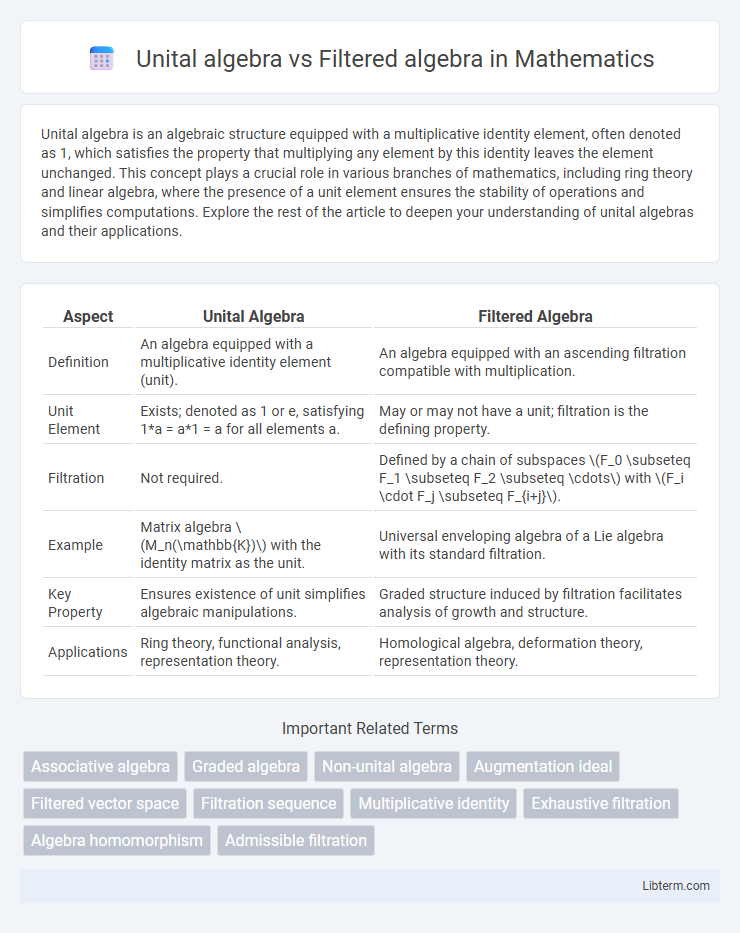
| Aspect | Unital Algebra | Filtered Algebra |
|---|---|---|
| Definition | An algebra equipped with a multiplicative identity element (unit). | An algebra equipped with an ascending filtration compatible with multiplication. |
| Unit Element | Exists; denoted as 1 or e, satisfying 1*a = a*1 = a for all elements a. | May or may not have a unit; filtration is the defining property. |
| Filtration | Not required. | Defined by a chain of subspaces \(F_0 \subseteq F_1 \subseteq F_2 \subseteq \cdots\) with \(F_i \cdot F_j \subseteq F_{i+j}\). |
| Example | Matrix algebra \(M_n(\mathbb{K})\) with the identity matrix as the unit. | Universal enveloping algebra of a Lie algebra with its standard filtration. |
| Key Property | Ensures existence of unit simplifies algebraic manipulations. | Graded structure induced by filtration facilitates analysis of growth and structure. |
| Applications | Ring theory, functional analysis, representation theory. | Homological algebra, deformation theory, representation theory. |
Introduction to Unital and Filtered Algebras
Unital algebras are algebraic structures equipped with a multiplicative identity element, enabling well-defined operations that include unity within the algebra. Filtered algebras, by contrast, are characterized by a hierarchical structure defined through an ascending chain of subspaces compatible with algebra multiplication, allowing systematic control over complexity and gradation. These foundational concepts are essential in advanced algebraic studies, particularly in understanding how algebraic systems can be organized and manipulated through unity and filtration properties.
Defining Unital Algebras
Unital algebras are algebraic structures equipped with a multiplicative identity element, ensuring the existence of an element \(1_A\) such that for any \(a\) in the algebra \(A\), the equation \(1_A \cdot a = a \cdot 1_A = a\) holds. In contrast, filtered algebras are vector spaces with a nested sequence of subspaces that respect the algebra multiplication but do not necessarily contain a multiplicative identity. Defining unital algebras requires explicitly specifying the unit element, which plays a crucial role in algebraic operations and homomorphisms, while filtered algebras prioritize graded or filtered structures without mandating a unit.
Understanding Filtered Algebras
Filtered algebras are algebraic structures equipped with an increasing sequence of subspaces that respect the algebra multiplication, allowing for a graded perspective on algebraic complexity and growth. Unlike unital algebras, which emphasize the presence of a multiplicative identity element, filtered algebras provide a framework to study algebraic objects via filtrations that capture layers of structure and complexity. These filtrations enable deep insights into deformation theory, representations, and homological properties by connecting graded algebras to their filtered counterparts.
Key Structural Differences
Unital algebras possess a multiplicative identity element that acts as a neutral element for algebra multiplication, enabling direct manipulation of algebraic units. Filtered algebras, conversely, are equipped with an increasing filtration sequence of subspaces that respects algebra multiplication, allowing graded structures and convergence studies without necessarily including a unit. The key structural difference lies in unital algebras' explicit identity element versus filtered algebras' layered subspace organization governing algebraic operations.
Algebraic Properties Comparison
Unital algebras feature a multiplicative identity element that facilitates algebraic operations such as inversion and simplifies module theory, while filtered algebras are equipped with an ascending filtration compatible with multiplication, enabling the study of graded structures and deformation theory. The inclusion of a unit in unital algebras ensures the existence of identity morphisms, whereas filtered algebras emphasize hierarchical layer structures leading to associated graded algebras. Both structures are fundamental in noncommutative geometry and representation theory, with unitality impacting algebra homomorphisms and filteredness allowing spectral sequence analysis.
Examples of Unital Algebras
Unital algebras are algebraic structures equipped with a multiplicative identity element, such as the algebra of nxn matrices over a field, polynomial algebras with unity, and group algebras where the identity corresponds to the group identity. Filtered algebras, in contrast, possess a chain of subspaces organized by degree but may lack a global multiplicative identity. Examples of unital algebras include matrix algebras M_n(K), polynomial rings K[x], and complex group algebras C[G], all featuring a clear unit element critical for algebraic operations and homomorphisms.
Examples of Filtered Algebras
Filtered algebras are algebraic structures equipped with an increasing sequence of subspaces that respect the multiplication operation, offering a way to study their complexity layer by layer. A classic example is the algebra of differential operators on a manifold, where the filtration is given by the order of the operators, allowing precise control over their algebraic properties. Another prominent example includes the universal enveloping algebra of a Lie algebra, filtered by the degree of tensor products, facilitating connections between Lie algebras and associative algebras.
Applications in Mathematics and Physics
Unital algebras form the foundation of associative algebraic structures with a multiplicative identity, essential in ring theory, module theory, and representation theory for modeling symmetries and conserved quantities in quantum mechanics. Filtered algebras, structured by increasing sequences of subspaces, enable the study of graded objects and deformation theory, playing a crucial role in understanding the algebraic structure of differential operators and the semiclassical analysis in mathematical physics. Both concepts underpin advanced topics such as the representation of Lie algebras, quantization procedures, and the formulation of physical observables in field theories.
Advantages and Limitations
Unital algebras provide a well-defined identity element that simplifies the construction of modules and ensures the existence of multiplicative inverses in certain subalgebras, enhancing algebraic manipulations and categorical equivalences. Filtered algebras offer a graded structure enabling the study of algebraic properties via associated graded algebras, facilitating deformation theory and homological computations. Unital algebras may lack the nuanced structure needed for analyzing algebra deformations, while filtered algebras can be more complex to handle computationally and may obscure explicit multiplicative identities.
Conclusion: Choosing Between Unital and Filtered Algebras
Choosing between unital and filtered algebras depends on the algebraic structure and application context. Unital algebras provide a multiplicative identity essential for module theory and representation, while filtered algebras offer a graded approach that facilitates the study of deformations and spectral sequences. The decision hinges on whether the emphasis is on maintaining unity for algebraic operations or leveraging filtration to analyze layered structures and convergence properties.
Unital algebra Infographic
 libterm.com
libterm.com