Sheaf theory provides a powerful framework in mathematics for systematically tracking local data attached to the open sets of a topological space and their consistency on overlaps. It plays a crucial role in fields such as algebraic geometry, differential topology, and complex analysis by enabling the study of global properties through local information. Explore the rest of this article to understand how sheaf theory can deepen your insight into modern mathematical structures.
Table of Comparison
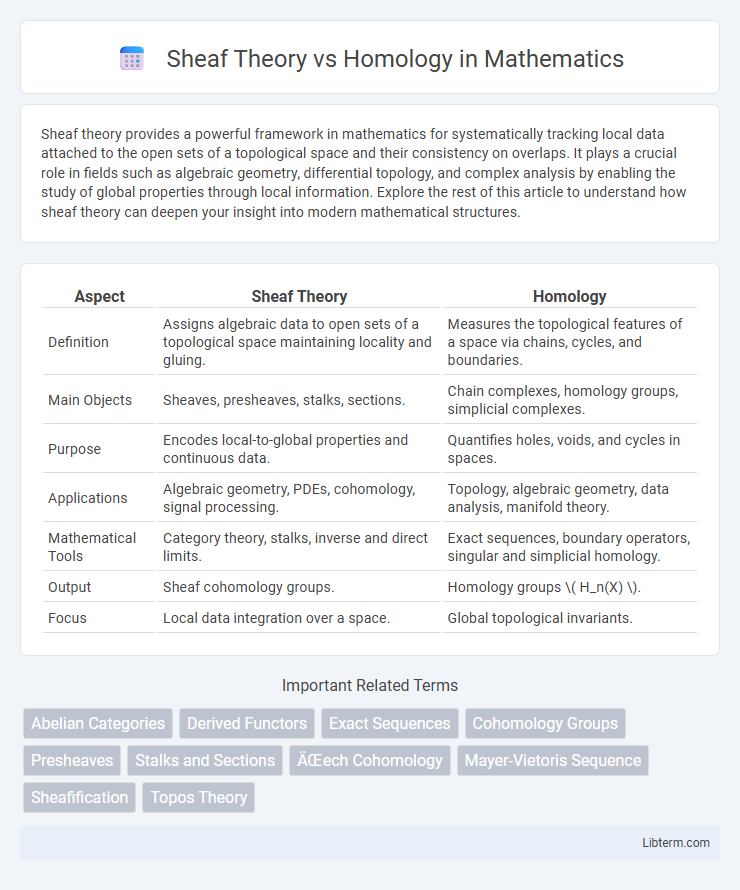
| Aspect | Sheaf Theory | Homology |
|---|---|---|
| Definition | Assigns algebraic data to open sets of a topological space maintaining locality and gluing. | Measures the topological features of a space via chains, cycles, and boundaries. |
| Main Objects | Sheaves, presheaves, stalks, sections. | Chain complexes, homology groups, simplicial complexes. |
| Purpose | Encodes local-to-global properties and continuous data. | Quantifies holes, voids, and cycles in spaces. |
| Applications | Algebraic geometry, PDEs, cohomology, signal processing. | Topology, algebraic geometry, data analysis, manifold theory. |
| Mathematical Tools | Category theory, stalks, inverse and direct limits. | Exact sequences, boundary operators, singular and simplicial homology. |
| Output | Sheaf cohomology groups. | Homology groups \( H_n(X) \). |
| Focus | Local data integration over a space. | Global topological invariants. |
Introduction to Sheaf Theory and Homology
Sheaf Theory provides a framework for systematically tracking local data attached to the open sets of a topological space and their compatibility on overlaps, enabling a nuanced study of geometric and algebraic structures. Homology, on the other hand, quantifies topological spaces by associating sequences of abelian groups or modules that capture global features such as holes and voids. While Homology offers invariants that classify spaces up to homotopy, Sheaf Theory generalizes this by encoding local-to-global interactions, which are essential in areas like algebraic geometry and differential topology.
Historical Background and Mathematical Context
Sheaf theory, developed in the mid-20th century by Jean Leray and further advanced by Alexander Grothendieck, originated as a tool to systematically manage local data glued together across topological spaces, primarily in algebraic geometry. Homology, stemming from earlier works by Henri Poincare in the late 19th century, provides algebraic invariants that classify topological spaces by measuring holes of different dimensions. Both frameworks serve to translate geometric intuition into algebraic structures, with sheaf theory enabling finer local-to-global analysis while homology captures global topological features.
Core Definitions: Sheaves and Homology
Sheaf theory studies sheaves, which are data structures assigning algebraic objects like sets or modules to open subsets of a topological space, capturing local-to-global information. Homology involves functors that assign sequences of abelian groups or modules to topological spaces, measuring holes or cycles via boundary maps in chain complexes. Core definitions differentiate sheaves as tools encoding local data with gluing conditions, whereas homology groups quantify topological invariants reflecting global geometric structure.
Fundamental Concepts: Presheaves, Sheafification, and Chain Complexes
Presheaves assign algebraic structures to open sets and restrict along inclusions, serving as the foundation for sheaf theory. Sheafification refines presheaves to satisfy locality and gluing axioms, producing sheaves that encode local-to-global data coherence. Chain complexes, central to homology, organize abelian groups or modules with boundary maps, enabling the computation of homological invariants that measure topological features.
Key Differences in Approach and Application
Sheaf theory systematically organizes local data attached to open sets of a topological space, emphasizing the assignment of algebraic structures and their compatibility on overlaps, which is crucial in algebraic geometry and logic. Homology, on the other hand, computes global topological invariants by analyzing cycles and boundaries within chain complexes, playing a key role in algebraic topology and geometric analysis. While sheaf theory captures local-to-global principles through exact sequences and derived functors, homology focuses on the quantitative classification of space features like holes and connectedness.
Sheaf Cohomology vs Classical Homology
Sheaf cohomology provides a flexible framework for studying topological spaces by associating algebraic invariants to open covers and their sections, capturing local-to-global properties that classical homology often misses. Unlike classical homology, which analyzes cycles and boundaries in simplicial complexes or singular spaces, sheaf cohomology can handle more refined geometric data through derived functors of global section functors on sheaves. This makes sheaf cohomology particularly powerful in algebraic geometry and complex manifolds, where local properties and obstructions influence global topological and analytical structures.
Examples: Sheaf Theory and Homology in Algebraic Topology
Sheaf theory in algebraic topology provides a framework for systematically tracking local algebraic data attached to open subsets of a topological space, such as assigning groups of sections to each open set and analyzing their local-to-global properties. Homology, by contrast, assigns algebraic invariants like homology groups to a topological space, capturing global topological features such as holes and connectivity. For example, sheaf cohomology can refine classical homology by incorporating local information, while singular homology focuses on chain complexes of continuous maps from simplices, illustrating distinct but complementary approaches to studying topological spaces.
Computational Methods and Tools
Sheaf theory and homology offer complementary computational methods in topological data analysis, with sheaf theory providing a framework for local-to-global data integration while homology focuses on global topological features through cycle detection. Computational tools like sheaf cohomology algorithms leverage cellular sheaves for efficient multi-scale data fusion, whereas homology computations often utilize persistent homology algorithms implemented in software such as GUDHI, Dionysus, and Ripser. Advances in combinatorial sheaf theory and parallelized homology computation enable scalable analysis of complex datasets in fields like sensor networks and shape recognition.
Modern Developments and Interactions
Modern developments in Sheaf Theory and Homology emphasize their deep interaction through derived category frameworks and persistent homology advancements. Sheaf-theoretic methods now facilitate local-to-global data analysis in topological spaces, while homological techniques extend to computational topology and data science contexts. This synergy enables refined invariants and novel applications in areas such as sensor networks, image processing, and topological data analysis.
Conclusion: Choosing Between Sheaf Theory and Homology
Choosing between Sheaf Theory and Homology depends on the complexity of the topological space and the type of data analysis required. Sheaf Theory excels in managing local-to-global data relationships and provides a flexible framework for analyzing varying data over spaces, while Homology offers straightforward, computable invariants that summarize global topological features. For applications requiring detailed local information combined with global consistency, Sheaf Theory is preferable; for coarse global topological classification and computational efficiency, Homology is more suitable.
Sheaf Theory Infographic
 libterm.com
libterm.com