Compact closed categories provide a powerful framework in category theory where every object has a dual, enabling the representation of processes like quantum entanglement and information flow. This structure facilitates elegant mathematical modeling of complex systems by allowing morphisms to be treated as reversible transformations. Discover how compact closed categories can enhance your understanding of both theoretical and applied mathematics by exploring the detailed concepts in the rest of this article.
Table of Comparison
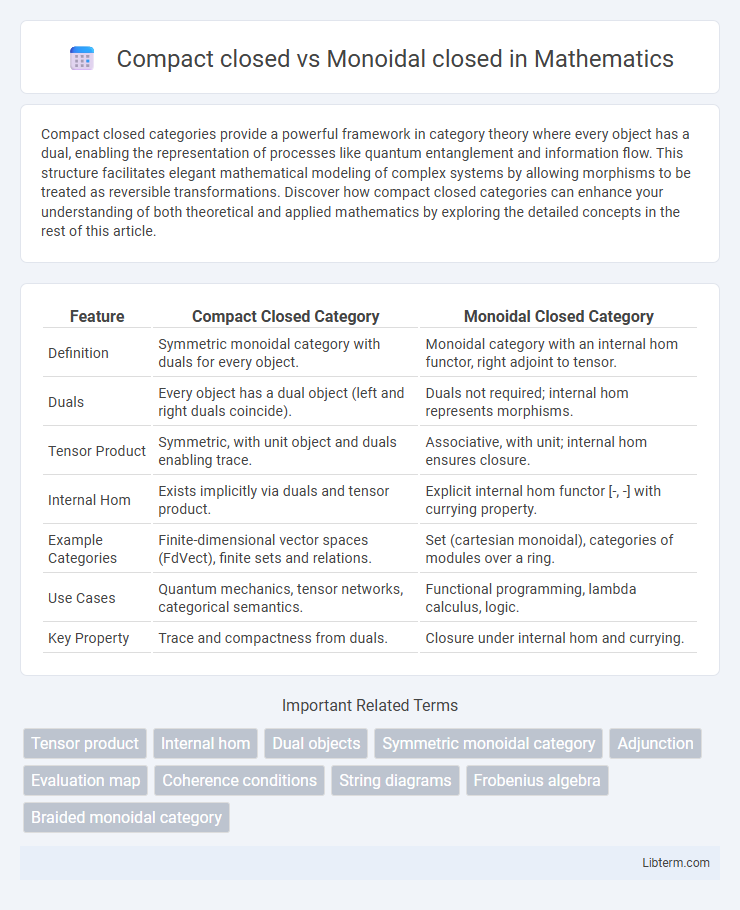
| Feature | Compact Closed Category | Monoidal Closed Category |
|---|---|---|
| Definition | Symmetric monoidal category with duals for every object. | Monoidal category with an internal hom functor, right adjoint to tensor. |
| Duals | Every object has a dual object (left and right duals coincide). | Duals not required; internal hom represents morphisms. |
| Tensor Product | Symmetric, with unit object and duals enabling trace. | Associative, with unit; internal hom ensures closure. |
| Internal Hom | Exists implicitly via duals and tensor product. | Explicit internal hom functor [-, -] with currying property. |
| Example Categories | Finite-dimensional vector spaces (FdVect), finite sets and relations. | Set (cartesian monoidal), categories of modules over a ring. |
| Use Cases | Quantum mechanics, tensor networks, categorical semantics. | Functional programming, lambda calculus, logic. |
| Key Property | Trace and compactness from duals. | Closure under internal hom and currying. |
Introduction to Closed Categories
Closed categories generalize the notion of function spaces, enabling internal hom-objects that represent morphisms between objects within the category itself. Compact closed categories are a special type of symmetric monoidal closed categories characterized by the existence of duals for every object, allowing a strong form of duality and trace operations. Monoidal closed categories provide an internal hom-functor compatible with the monoidal structure, facilitating currying and richer structural transformations without necessarily requiring duals for all objects.
Understanding Monoidal Closed Categories
Monoidal closed categories feature an internal hom-functor that represents morphisms as objects within the category, enabling currying and internalization of function spaces essential for categorical logic and type theory. Unlike compact closed categories, which require each object to have a dual and create a rigid categorical structure, monoidal closed categories allow for a more flexible tensor product without necessitating dual objects. This internal hom-structure supports enriched category theory and models of linear logic by expressing morphisms as objects, making monoidal closed categories foundational for understanding resource-sensitive computations.
Defining Compact Closed Categories
Compact closed categories are monoidal categories where every object has a dual with morphisms satisfying specific coherence conditions, enabling processes like trace and feedback in categorical contexts. These categories inherently support the notion of duality through cap and cup morphisms, making them fundamental in areas such as quantum computing and categorical logic. Monoidal closed categories generalize this structure by allowing internal hom-objects without requiring duals for every object, thus providing a broader framework for modeling function spaces within categorical settings.
Key Differences Between Compact and Monoidal Closed
Compact closed categories feature a duality for every object, enabling a morphism to have both left and right adjoints, which facilitates processes like quantum teleportation. Monoidal closed categories provide an internal hom-functor, allowing the representation of morphisms as objects within the category, essential for modeling function spaces in logic and computer science. The key distinction lies in compact closure requiring dual objects and morphisms with duals, while monoidal closure emphasizes internal hom-objects without necessitating duals for all objects.
Structure and Properties of Monoidal Closed Categories
Monoidal closed categories feature an internal hom-functor that provides a right adjoint to the tensor product, enabling the expression of function spaces within the category. Their structure supports currying and evaluation morphisms, reflecting a rich interplay between tensor products and internal homs. In contrast, compact closed categories impose additional duality conditions where every object has a dual, leading to a symmetric, self-dual tensor structure with trace and feedback operations vital for diagrammatic reasoning in quantum computing and categorical semantics.
Duality in Compact Closed Categories
Compact closed categories exhibit a strong form of duality where every object has a dual equipped with unit and counit morphisms satisfying the snake equations, enabling powerful notions of trace and feedback. Monoidal closed categories possess an internal hom-functor allowing the representation of morphisms as objects, but generally lack a global dual for every object, making their notion of duality weaker and less symmetric. The duality in compact closed categories facilitates elegant categorical interpretations of quantum mechanics and topological invariants, contrasting with the more functionally oriented structure of monoidal closed categories.
Examples of Monoidal Closed Categories
Monoidal closed categories include examples such as the category of sets with Cartesian product, where the internal hom is given by the set of functions, and the category of vector spaces over a field equipped with the tensor product, featuring the space of linear maps as the internal hom. Another significant example is the category of modules over a commutative ring, which forms a monoidal closed category under the tensor product with the internal hom given by the Hom functor. These examples illustrate how monoidal closure generalizes the notion of function spaces and linear maps within various algebraic and categorical contexts.
Applications of Compact Closed Categories
Compact closed categories are crucial in quantum computing for modeling entangled states and quantum protocols, leveraging their dual objects and morphisms structure to represent complex processes. These categories also find applications in linguistics, particularly in categorical compositional distributional semantics, where they provide a formal framework to interpret natural language syntax and semantics. In contrast, monoidal closed categories are essential in lambda calculus and type theory, enabling function spaces within the categorical structure but lacking the inherent duality that facilitates quantum and linguistic applications.
Compact Closed vs Monoidal Closed: Comparative Table
Compact closed categories feature dual objects with morphisms that satisfy yanking equations, enabling a graphical calculus with cups and caps, while monoidal closed categories provide an internal hom-functor establishing an adjunction between tensor products and hom-objects. Compact closed structures guarantee every object has a dual, making them pivotal in quantum computing and diagrammatic reasoning, whereas monoidal closed categories emphasize the existence of right adjoints to the tensor product, important in categorical logic and lambda calculus. The comparative table highlights that compact closed categories are symmetric with duals and strict yanking, while monoidal closed categories relax symmetry and focus on internal hom-functors without necessarily having dual objects.
Conclusion and Future Perspectives
Compact closed categories provide a powerful framework for modeling duality and tensor operations with strong symmetry properties, making them well-suited for applications in quantum computing and linguistic semantics. Monoidal closed categories extend this by incorporating internal hom-functors, enabling richer functional representations and a deeper understanding of morphism composition in categorical structures. Future research may explore hybrid models that leverage the strengths of both frameworks to advance computational semantics, quantum protocols, and categorical logic, fostering expanded applications in computer science and mathematics.
Compact closed Infographic
 libterm.com
libterm.com