A coset is a fundamental concept in group theory, representing a subset formed by multiplying all elements of a subgroup by a fixed group element. Cosets play a crucial role in understanding group structure, partitioning a group into equal-sized, non-overlapping sets that reveal symmetry and simplify complex problems. Explore the rest of the article to uncover how cosets influence advanced algebraic concepts and their practical applications.
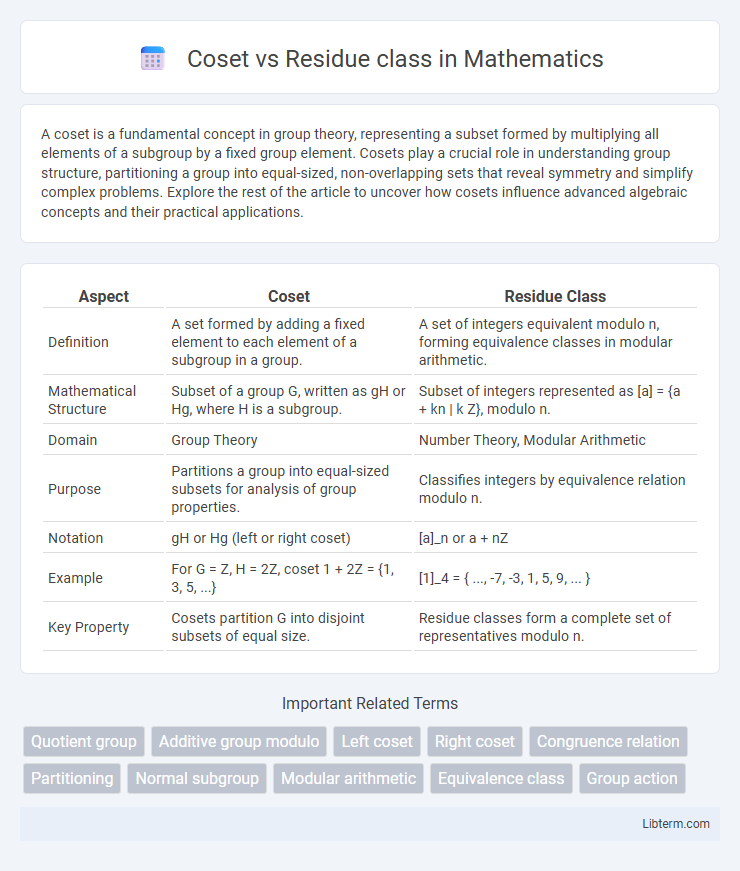
Table of Comparison
| Aspect | Coset | Residue Class |
|---|---|---|
| Definition | A set formed by adding a fixed element to each element of a subgroup in a group. | A set of integers equivalent modulo n, forming equivalence classes in modular arithmetic. |
| Mathematical Structure | Subset of a group G, written as gH or Hg, where H is a subgroup. | Subset of integers represented as [a] = {a + kn | k Z}, modulo n. |
| Domain | Group Theory | Number Theory, Modular Arithmetic |
| Purpose | Partitions a group into equal-sized subsets for analysis of group properties. | Classifies integers by equivalence relation modulo n. |
| Notation | gH or Hg (left or right coset) | [a]_n or a + nZ |
| Example | For G = Z, H = 2Z, coset 1 + 2Z = {1, 3, 5, ...} | [1]_4 = { ..., -7, -3, 1, 5, 9, ... } |
| Key Property | Cosets partition G into disjoint subsets of equal size. | Residue classes form a complete set of representatives modulo n. |
Introduction to Cosets and Residue Classes
Cosets arise in group theory as subsets formed by multiplying all elements of a subgroup by a fixed group element, creating left or right cosets depending on the multiplication side. Residue classes, fundamental in modular arithmetic, partition integers into equivalence classes based on congruence relations modulo a given integer. Both cosets and residue classes serve as key structures in abstract algebra, enabling the study of quotient groups and modular systems.
Defining Cosets in Group Theory
In group theory, a coset is defined as the set formed by multiplying a fixed element from the group with each element of a subgroup, resulting in either a left coset \( gH = \{gh : h \in H\} \) or a right coset \( Hg = \{hg : h \in H\} \). Each coset represents a distinct equivalence class under the equivalence relation induced by the subgroup, partitioning the group into disjoint subsets of equal size. Residue classes in modular arithmetic serve as a specific example of cosets, illustrating the broader concept in abstract algebra that links subgroup structure to the partitioning of groups.
Understanding Residue Classes in Modular Arithmetic
Residue classes in modular arithmetic represent the set of all integers congruent to a specific integer modulo n, forming equivalence classes under the modulo relation. These classes partition the integers into distinct subsets where each element shares the same remainder upon division by n. Understanding residue classes is fundamental to modular arithmetic, enabling simplified calculations and applications in number theory, cryptography, and algebraic structures.
Mathematical Notation and Formal Definitions
A coset of a subgroup \( H \) in a group \( G \) is formally defined as the set \( gH = \{ gh \mid h \in H \} \) for a fixed element \( g \in G \), representing left cosets, or \( Hg = \{ hg \mid h \in H \} \) for right cosets. A residue class modulo \( n \), denoted as \( [a]_n = \{ a + kn \mid k \in \mathbb{Z} \} \), forms an equivalence class in the quotient ring \( \mathbb{Z}/n\mathbb{Z} \), where elements are congruent modulo \( n \). Cosets generalize subgroup partitioning in arbitrary groups, whereas residue classes specifically characterize equivalence under modular arithmetic within integer rings.
Key Differences Between Cosets and Residue Classes
Cosets arise in group theory as subsets formed by multiplying a fixed element with a subgroup, while residue classes partition integers based on congruence relations modulo a fixed number. Cosets reflect algebraic structures and vary with subgroup choice, whereas residue classes are equivalence classes central to modular arithmetic. The primary distinction lies in cosets' dependence on group operations and subgroups, contrasting with residue classes' basis in integer modular equivalence.
Examples of Cosets in Abstract Algebra
In abstract algebra, cosets are formed by adding a fixed element to each member of a subgroup, such as in the group of integers under addition where the subgroup 2Z creates cosets like 0 + 2Z and 1 + 2Z. Another example occurs in the symmetric group S3, where the subgroup generated by a transposition leads to distinct left cosets partitioning the group. These examples illustrate how cosets provide a fundamental way to analyze group structure and form quotient groups through equivalence relations.
Illustrative Examples of Residue Classes
Residue classes illustrate equivalence relations in modular arithmetic, where numbers are grouped by their remainders upon division by a fixed modulus; for example, modulo 5, the residue class of 2 includes {..., -8, -3, 2, 7, 12, ...} as all these numbers leave a remainder of 2 when divided by 5. In contrast, a coset in group theory represents a set formed by multiplying all elements of a subgroup by a fixed element, such as aH = {ah | h H}, where a is an element of the group and H is a subgroup. Residue classes provide a clear illustration of partitioning integers into disjoint sets based on modular equivalence, serving as fundamental examples in number theory and abstract algebra.
Applications of Cosets in Mathematics
Cosets play a crucial role in group theory, particularly in the study of quotient groups and Lagrange's theorem, where they help determine the index of a subgroup and partition a group into equal-sized subsets. In number theory, cosets correspond to residue classes modulo an integer, facilitating modular arithmetic and the construction of finite fields. Applications of cosets extend to coding theory, cryptography, and the analysis of symmetry in algebraic structures, enabling efficient algorithms and classification of mathematical objects.
Practical Uses of Residue Classes
Residue classes play a critical role in modular arithmetic, enabling practical applications such as cryptography, error detection, and computer science algorithms. Unlike cosets, which are used to describe partitions of groups in abstract algebra, residue classes simplify computations by grouping integers with the same remainder when divided by a modulus. This property is essential for hashing functions, random number generation, and solving congruences efficiently.
Conclusion: Comparing Cosets and Residue Classes
Cosets and residue classes both partition a group or ring into equivalence classes but differ in their underlying algebraic structure and application. Cosets arise from subgroup relations in group theory, highlighting symmetry and structure, while residue classes form from ideal relations in ring theory, crucial for modular arithmetic and number theory. Understanding their distinctions enhances algebraic insight and supports advanced problem-solving in abstract algebra contexts.
Coset Infographic
 libterm.com
libterm.com