Eisenstein series are a fundamental concept in the theory of modular forms, playing a key role in number theory and complex analysis. They are defined as infinite series that exhibit remarkable transformation properties under the action of the modular group, making them essential for studying arithmetic functions and elliptic curves. Explore the rest of the article to understand how Eisenstein series connect to advanced mathematical topics and their applications.
Table of Comparison
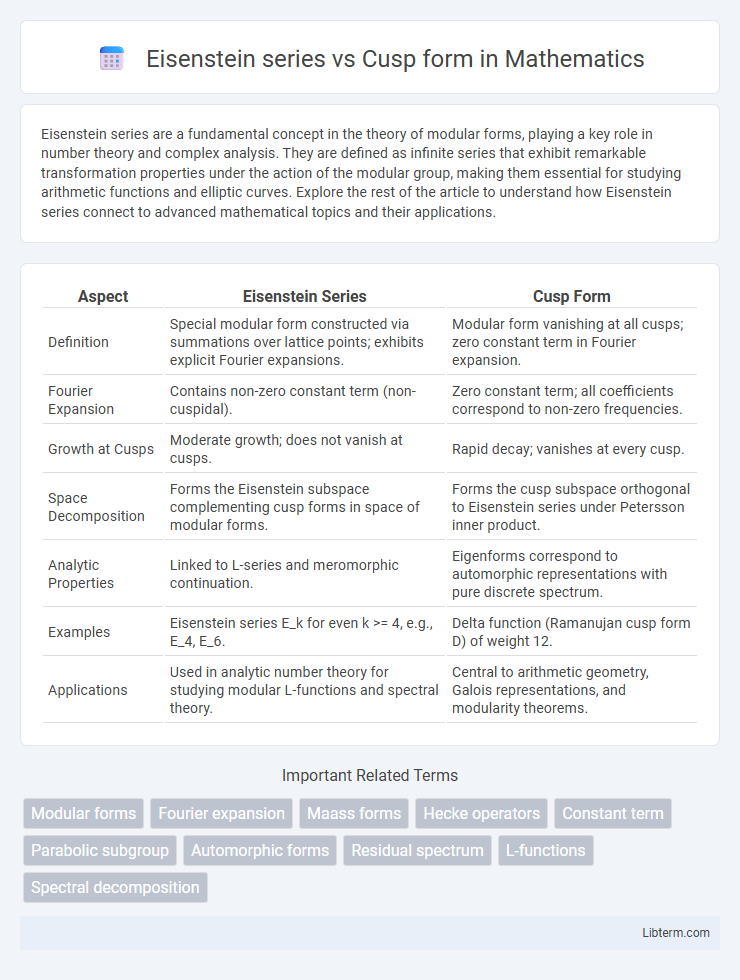
| Aspect | Eisenstein Series | Cusp Form |
|---|---|---|
| Definition | Special modular form constructed via summations over lattice points; exhibits explicit Fourier expansions. | Modular form vanishing at all cusps; zero constant term in Fourier expansion. |
| Fourier Expansion | Contains non-zero constant term (non-cuspidal). | Zero constant term; all coefficients correspond to non-zero frequencies. |
| Growth at Cusps | Moderate growth; does not vanish at cusps. | Rapid decay; vanishes at every cusp. |
| Space Decomposition | Forms the Eisenstein subspace complementing cusp forms in space of modular forms. | Forms the cusp subspace orthogonal to Eisenstein series under Petersson inner product. |
| Analytic Properties | Linked to L-series and meromorphic continuation. | Eigenforms correspond to automorphic representations with pure discrete spectrum. |
| Examples | Eisenstein series E_k for even k >= 4, e.g., E_4, E_6. | Delta function (Ramanujan cusp form D) of weight 12. |
| Applications | Used in analytic number theory for studying modular L-functions and spectral theory. | Central to arithmetic geometry, Galois representations, and modularity theorems. |
Introduction to Eisenstein Series and Cusp Forms
Eisenstein series are complex analytic functions defined on the upper half-plane, constructed using sums over lattice points that exhibit modular properties under SL(2, Z) transformations. Cusp forms are a subclass of modular forms characterized by their vanishing behavior at all cusps, exhibiting rapid decay that distinguishes them from Eisenstein series, which do not vanish at cusps. Both Eisenstein series and cusp forms play crucial roles in the spectral decomposition of automorphic forms and are fundamental objects in the theory of modular forms and number theory.
Historical Background and Development
Eisenstein series and cusp forms emerged from the foundational work in the theory of modular forms during the 19th and early 20th centuries, with Eisenstein series initially studied by Gotthold Eisenstein as explicit examples of modular forms exhibiting non-vanishing Fourier coefficients at infinity. Cusp forms were later characterized to vanish at all cusps, refining the modular forms space and gaining prominence through the work of Henri Poincare and Erich Hecke, who explored their spectral and arithmetic properties. The development of the theory was significantly advanced by Atle Selberg's trace formula and the modularity theorems, which established deeper connections between Eisenstein series, cusp forms, and automorphic representations.
Definitions: Eisenstein Series
Eisenstein series are a type of modular form defined by summing a complex function over a lattice in the upper half-plane, often expressed as \( E_k(z) = \sum_{(m,n)\neq(0,0)} (mz + n)^{-k} \) for even integer weights \( k > 2 \). Unlike cusp forms, Eisenstein series do not vanish at the cusps and represent non-cuspidal elements in the space of modular forms. They play a crucial role in number theory by providing explicit examples of modular forms with known Fourier expansions and are essential in the study of automorphic forms and L-functions.
Definitions: Cusp Forms
Cusp forms are a subclass of modular forms characterized by their vanishing behavior at all cusps of the modular curve, meaning they approach zero at every boundary point of the modular domain. Unlike Eisenstein series, cusp forms possess rapid decay at infinity, ensuring their Fourier expansions lack constant terms. This property makes cusp forms essential in number theory and representation theory due to their connection with L-functions and automorphic representations.
Fourier Expansions: Comparison and Contrast
Eisenstein series feature Fourier expansions with non-vanishing constant terms, reflecting their non-cuspidal nature and contributions from parabolic elements in modular forms theory. In contrast, cusp forms have Fourier expansions with zero constant terms, ensuring rapid decay at cusps and emphasizing their square-integrable automorphic properties. The difference in these Fourier coefficients signifies the fundamental spectral decomposition of modular forms into continuous components from Eisenstein series and discrete parts from cusp forms.
Analytic Properties of Eisenstein Series
Eisenstein series exhibit meromorphic continuation and functional equations across the complex plane, contrasting the cusp forms which are entire and vanish at cusps. Their Fourier expansions include constant terms reflecting non-trivial residues linked to special values of L-functions, while cusp forms have zero constant terms. The analytic behavior of Eisenstein series is crucial in understanding spectral decomposition on modular curves and automorphic representations.
Analytic Properties of Cusp Forms
Cusp forms are holomorphic functions on the upper half-plane that vanish at all cusps, characterizing their rapid decay and square-integrability, which contrasts with Eisenstein series that exhibit slower polynomial growth and continuous spectra. The analytic properties of cusp forms include their role as eigenfunctions of Hecke operators, possessing discrete spectrum and Fourier expansions with rapidly decreasing coefficients, essential for modular form theory and number theory applications. Their L-functions satisfy functional equations and analytic continuation, deeply connected to automorphic representations and the Langlands program.
Orthogonality and Decomposition in Modular Forms
Eisenstein series and cusp forms form an orthogonal basis in the space of modular forms under the Petersson inner product, allowing a modular form to be uniquely decomposed into a sum of an Eisenstein series and a cusp form. This decomposition exploits the orthogonality between non-cuspidal Eisenstein series, which have nonzero constant terms at cusps, and cusp forms, which vanish at all cusps. The orthogonality property facilitates explicit spectral expansions crucial for analytic number theory and automorphic form studies.
Applications in Number Theory and Automorphic Forms
Eisenstein series and cusp forms play crucial roles in number theory by encoding arithmetic information through Fourier coefficients, with Eisenstein series connecting to divisor functions and cusp forms relating to prime distributions via L-functions. In automorphic forms, Eisenstein series serve as building blocks for constructing non-cuspidal automorphic representations, while cusp forms correspond to discrete spectrum elements essential for understanding modularity and Langlands program connections. Their applications extend to proving cases of the Ramanujan-Petersson conjecture and establishing deep links between elliptic curves and modular forms through the modularity theorem.
Conclusion: Key Differences and Interconnections
Eisenstein series are non-cuspidal modular forms characterized by their explicit Fourier expansions and connections to L-functions, while cusp forms vanish at all cusps and exhibit rapid decay, representing the space's orthogonal complement to Eisenstein series. The interconnection lies in their decomposition of the space of modular forms, where Eisenstein series capture the continuous spectrum and cusp forms correspond to discrete spectrum in the theory of automorphic forms. Understanding their key differences and relationships is fundamental in number theory and the spectral theory of modular forms.
Eisenstein series Infographic
 libterm.com
libterm.com