Understanding the concept of class in society reveals the layers of economic, social, and cultural distinctions that influence your lifestyle and opportunities. Social class shapes access to education, healthcare, and wealth distribution, affecting both personal identity and community dynamics. Explore the rest of the article to uncover how class impacts your daily life and societal structures.
Table of Comparison
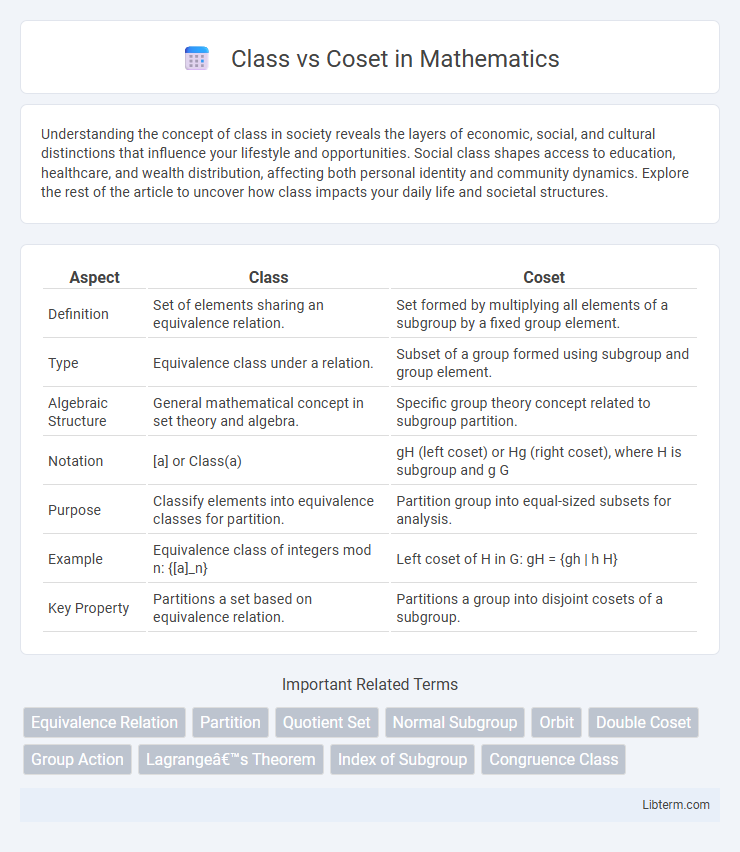
| Aspect | Class | Coset |
|---|---|---|
| Definition | Set of elements sharing an equivalence relation. | Set formed by multiplying all elements of a subgroup by a fixed group element. |
| Type | Equivalence class under a relation. | Subset of a group formed using subgroup and group element. |
| Algebraic Structure | General mathematical concept in set theory and algebra. | Specific group theory concept related to subgroup partition. |
| Notation | [a] or Class(a) | gH (left coset) or Hg (right coset), where H is subgroup and g G |
| Purpose | Classify elements into equivalence classes for partition. | Partition group into equal-sized subsets for analysis. |
| Example | Equivalence class of integers mod n: {[a]_n} | Left coset of H in G: gH = {gh | h H} |
| Key Property | Partitions a set based on equivalence relation. | Partitions a group into disjoint cosets of a subgroup. |
Understanding the Concept of Class in Mathematics
In mathematics, a class represents a collection of elements defined by a common property or equivalence relation, often used in set theory and category theory to group objects that share specific attributes. Unlike a coset, which is a subset formed by combining a fixed element with a subgroup in group theory, a class typically encompasses broader groupings that may not have subgroup structure. Understanding classes involves grasping their role in organizing elements into meaningful categories for analysis and comparison across various mathematical contexts.
Defining Coset: A Fundamental Group Theory Concept
A coset is formed by taking an element from a group and combining it with every element of a subgroup, creating a subset with uniform structure. Cosets can be left or right depending on how the element multiplies with the subgroup elements, central to partitioning groups into equal-sized non-overlapping parts. These structures are key for understanding quotient groups and play a crucial role in the study of group actions and symmetry.
Class vs Coset: Key Differences Explained
A class in group theory refers to a conjugacy class, which consists of elements related by inner automorphisms showing symmetry within the group, while a coset is formed by adding a fixed element to every element of a subgroup, representing a partition of the group into equal-sized subsets. Classes emphasize element equivalence under conjugation, crucial for analyzing group structure and representations, whereas cosets focus on subgroup partitions, key in factor group construction and Lagrange's theorem. Understanding these distinctions aids in exploring group actions, normality, and quotient groups.
Types of Groups and Their Relation to Classes and Cosets
Types of groups such as Abelian groups, cyclic groups, and normal groups exhibit distinct behaviors in relation to classes and cosets. In Abelian groups, left and right cosets coincide, making every coset a natural equivalence class under the subgroup relation. Normal subgroups generate well-defined quotient groups where cosets form equivalence classes essential to the group's quotient structure.
Examples of Classes in Algebra and Set Theory
In group theory, a left coset of a subgroup \( H \) in a group \( G \) is defined as \( gH = \{gh \mid h \in H\} \) for a fixed \( g \in G \), illustrating how elements of \( G \) are partitioned into disjoint subsets called cosets. In set theory, equivalence classes arise from an equivalence relation \( \sim \), where the equivalence class of an element \( a \) is \( [a] = \{ x \in S \mid x \sim a \} \), grouping elements related under \( \sim \). For example, in modular arithmetic the class of integers congruent to \( 1 \mod 3 \) forms an equivalence class, while in group theory, the cosets of subgroup \( \mathbb{Z}_3 \) in \( \mathbb{Z}_6 \) partition the group into distinct cosets like \( 0 + \mathbb{Z}_3 \) and \( 1 + \mathbb{Z}_3 \).
Real-World Applications of Cosets in Cryptography
Cosets play a critical role in cryptography by structuring information within algebraic groups to enhance security protocols. They enable efficient partitioning of groups into disjoint subsets, facilitating the design of error-correcting codes and secure key exchange methods. Unlike classes that group elements by conjugacy, cosets provide the mathematical foundation for implementing advanced cryptographic algorithms such as the Diffie-Hellman key exchange and elliptic curve cryptography.
The Role of Equivalence Relations in Forming Classes
Equivalence relations partition a set into distinct classes by grouping elements that share a specific equivalence property, ensuring each element belongs to exactly one class. In algebraic structures, a class formed by an equivalence relation corresponds to the set of elements equivalent under a given relation, such as congruence modulo a subgroup in group theory. This foundational role of equivalence relations underlies the formation of cosets, where each coset represents an equivalence class of group elements related by multiplication with a fixed subgroup element.
Cosets and Lagrange’s Theorem: An Essential Connection
Cosets partition a group into equal-sized, disjoint subsets formed by multiplying a fixed element with each element of a subgroup, highlighting the group's internal structure. Lagrange's Theorem states that the order of any subgroup divides the order of the entire finite group, and the number of distinct cosets corresponds to the index of the subgroup. This fundamental connection between cosets and subgroup orders enables crucial insights in group theory, including classifying groups and solving problems in algebraic structures.
Visualizing Class and Coset with Diagrams
Visualizing a class involves depicting equivalence classes as distinct clusters within a set, highlighting elements grouped by an equivalence relation. Cosets can be represented through diagrams showing a subgroup partitioning a group into equal-sized, non-overlapping subsets, emphasizing translational symmetry by a fixed element. These diagrams clarify the differences and interrelations by illustrating how classes partition sets, while cosets partition groups into structured, uniform pieces.
Common Misconceptions about Classes and Cosets
Many learners confuse equivalence classes with cosets, assuming both are interchangeable when classes emerge from equivalence relations and cosets specifically arise in group theory involving subgroups. Another common misconception is that all cosets form a group; only when the subgroup is normal do the cosets form a well-defined quotient group. It is also mistaken to believe that distinct cosets can overlap, whereas cosets partition the group into disjoint subsets.
Class Infographic
 libterm.com
libterm.com