A semidirect product is a fundamental concept in group theory that combines two groups into a new, more complex structure where one subgroup acts on the other via automorphisms. This construction is crucial for understanding how groups can be decomposed and analyzed through their subgroups. Explore the rest of the article to uncover how semidirect products influence symmetry and structure in algebraic systems.
Table of Comparison
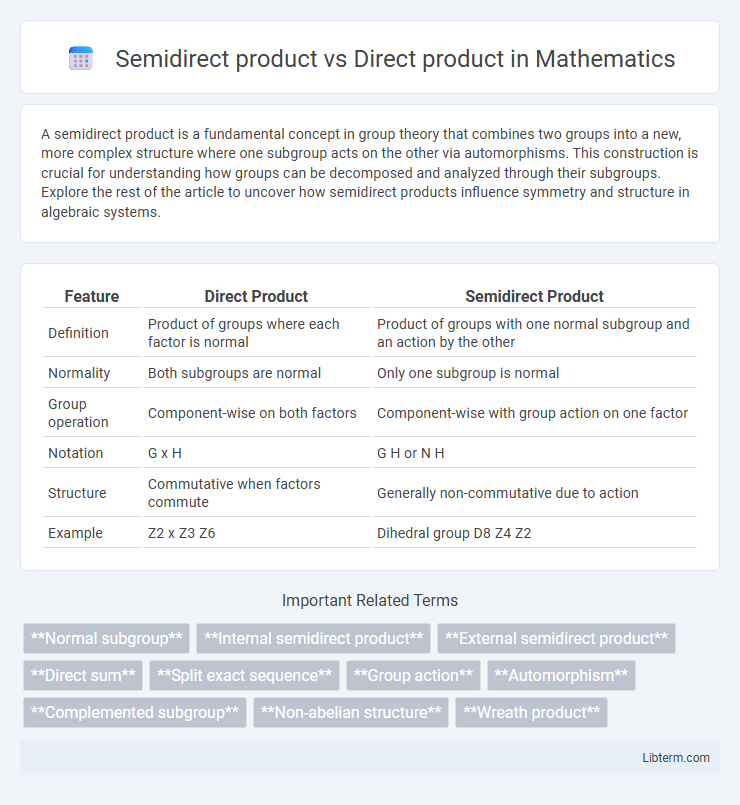
| Feature | Direct Product | Semidirect Product |
|---|---|---|
| Definition | Product of groups where each factor is normal | Product of groups with one normal subgroup and an action by the other |
| Normality | Both subgroups are normal | Only one subgroup is normal |
| Group operation | Component-wise on both factors | Component-wise with group action on one factor |
| Notation | G x H | G H or N H |
| Structure | Commutative when factors commute | Generally non-commutative due to action |
| Example | Z2 x Z3 Z6 | Dihedral group D8 Z4 Z2 |
Introduction to Group Products
The direct product of two groups G and H creates a new group where each element is an ordered pair (g, h) with group operations performed component-wise, preserving group structure independently. The semidirect product generalizes this by allowing a nontrivial group action of one group on the other, resulting in a product group whose operation reflects this interaction. Understanding these constructions is fundamental in group theory for analyzing complex group structures through simpler subgroups and their interactions.
Understanding Direct Product of Groups
The direct product of groups G and H, denoted G x H, consists of ordered pairs (g, h) where g G and h H, with group operation defined component-wise. This construction ensures that the subgroups G x {e_H} and {e_G} x H are normal and intersect trivially, enabling a straightforward combination of group structures without interaction beyond independent operations. Understanding the direct product is essential for decomposing complex groups into simpler components, facilitating analysis in group theory and applications such as symmetry groups and algebraic topology.
Defining Semidirect Product of Groups
The semidirect product of groups combines a normal subgroup \(N\) and a subgroup \(H\) such that the group operation incorporates a homomorphism from \(H\) to the automorphism group of \(N\), denoted \(\varphi: H \to \text{Aut}(N)\). Unlike the direct product where both subgroups commute and act independently, the semidirect product uses this action \(\varphi\) to define a multiplication \((n_1, h_1)(n_2, h_2) = (n_1 \varphi(h_1)(n_2), h_1 h_2)\). This structure allows more complex group compositions where \(H\) acts on \(N\), generalizing the direct product concept.
Key Differences Between Direct and Semidirect Products
The key differences between direct and semidirect products lie in the interaction of their subgroup structures and homomorphisms; a direct product requires both subgroups to be normal with trivial intersection, ensuring elements commute independently, while a semidirect product allows only one normal subgroup and incorporates a nontrivial action of one subgroup on the other via a homomorphism. In a direct product \(G = H \times K\), every element can be uniquely expressed as a product of elements from \(H\) and \(K\) with no twisting, whereas in a semidirect product \(G = H \rtimes K\), the subgroup \(K\) acts on \(H\) by automorphisms, introducing a structured non-commutativity. This distinction shapes the group's structure and applications, with direct products suitable for decomposable groups and semidirect products modeling extensions with internal symmetries.
Algebraic Properties and Structure
The direct product of groups combines two groups G and H into a new group G x H where each element pair commutes independently, preserving the individual group structures without interaction. In contrast, the semidirect product G H incorporates an action of H on G, resulting in a more complex structure where G is a normal subgroup but the overall group operation is twisted by the homomorphism from H into the automorphism group of G. This fundamental difference affects algebraic properties such as normality, commutativity, and subgroup structure, with the semidirect product allowing for non-abelian groups even when the component groups are abelian.
Examples of Direct Product Groups
The direct product of groups combines two groups \(G\) and \(H\) into a new group \(G \times H\), such as \(\mathbb{Z}_2 \times \mathbb{Z}_3\), which forms a group of order 6 with elements paired from each cyclic group. Classic examples include \(\mathbb{Z}_m \times \mathbb{Z}_n\), where the resulting group is cyclic if and only if \(m\) and \(n\) are coprime, illustrating the structural simplicity of direct products. Unlike semidirect products, direct products possess a normal subgroup in each factor, with the entire group decomposable into straightforward Cartesian products.
Examples of Semidirect Product Groups
The semidirect product group Z_6 Z_2 illustrates a classic example where the group Z_2 acts nontrivially on Z_6 by automorphisms, creating a non-abelian group structure differing from the direct product Z_6 x Z_2. Another example is the dihedral group D_8, realized as a semidirect product of Z_4 by Z_2, where Z_2 induces an inversion automorphism on Z_4. These examples emphasize the role of the twisting homomorphism in semidirect products, resulting in groups that are not just Cartesian products but richer algebraic structures.
Applications in Abstract Algebra
Semidirect products enable the construction of more complex groups by combining a normal subgroup with another group acting on it, crucial for analyzing symmetry groups and group extensions in abstract algebra. Direct products create groups whose elements operate independently, simplifying the study of group decompositions and facilitating computations in module theory. Applications of semidirect products are pivotal in classifying non-abelian groups and understanding automorphism groups, while direct products primarily aid in constructing larger groups from simpler components.
Criteria for Choosing Direct or Semidirect Product
Choosing between a direct product and a semidirect product hinges on the interaction between the underlying groups; direct products apply when both subgroups are normal and commute element-wise, ensuring a simple, component-wise group operation. Semidirect products become necessary if one subgroup is normal but the other acts non-trivially via automorphisms on it, introducing a more complex structure encoding an action. The decision criterion involves verifying normality conditions and whether the group extension splits trivially, guiding whether the group decomposes purely or via a nontrivial action.
Summary and Conclusion
The direct product of groups combines two groups into a new group where elements commute independently, preserving the original structures without interaction. The semidirect product generalizes this by allowing one group to act on the other via a homomorphism, enabling more complex group structures with nontrivial interactions. Understanding these differences is crucial in group theory applications, as semidirect products model symmetry groups and extension problems that direct products cannot capture.
Semidirect product Infographic
 libterm.com
libterm.com