Non-abelian simple groups are fundamental objects in group theory characterized by having no normal subgroups other than the trivial group and themselves, and they do not commute under group operation. These groups play a crucial role in the classification of finite simple groups and have applications in various mathematical and physical theories. Discover more about the properties and significance of non-abelian simple groups in the rest of the article.
Table of Comparison
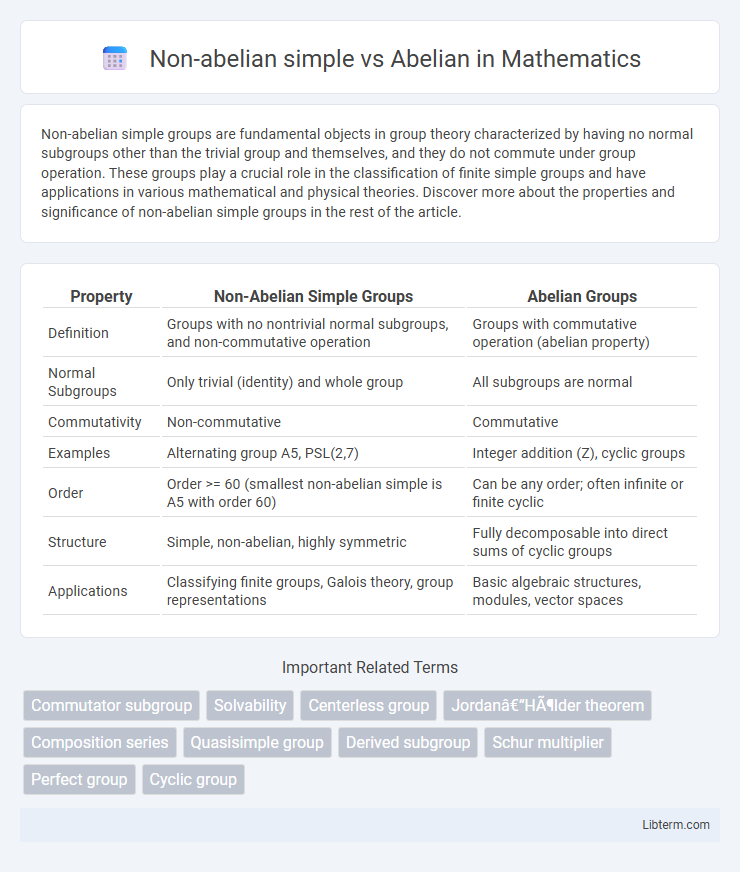
| Property | Non-Abelian Simple Groups | Abelian Groups |
|---|---|---|
| Definition | Groups with no nontrivial normal subgroups, and non-commutative operation | Groups with commutative operation (abelian property) |
| Normal Subgroups | Only trivial (identity) and whole group | All subgroups are normal |
| Commutativity | Non-commutative | Commutative |
| Examples | Alternating group A5, PSL(2,7) | Integer addition (Z), cyclic groups |
| Order | Order >= 60 (smallest non-abelian simple is A5 with order 60) | Can be any order; often infinite or finite cyclic |
| Structure | Simple, non-abelian, highly symmetric | Fully decomposable into direct sums of cyclic groups |
| Applications | Classifying finite groups, Galois theory, group representations | Basic algebraic structures, modules, vector spaces |
Introduction to Abelian and Non-Abelian Groups
Abelian groups are algebraic structures where the group operation is commutative, meaning the order of elements does not affect the outcome, exemplified by integer addition under standard rules. Non-Abelian groups, in contrast, exhibit non-commutative operations, with matrix multiplication in the symmetry group of a square being a classic example. Simple groups, both Abelian and non-Abelian, serve as fundamental building blocks in group theory, with non-Abelian simple groups playing a crucial role in the classification of finite groups due to their complex structure and lack of nontrivial normal subgroups.
Defining Simple Groups: Abelian and Non-Abelian
Simple groups are defined by having no nontrivial normal subgroups, with Abelian simple groups being precisely the cyclic groups of prime order. Non-Abelian simple groups, in contrast, exhibit more complex structures with no proper, nontrivial normal subgroups, playing a critical role in the classification of finite simple groups. While Abelian simple groups are commutative and structurally straightforward, non-Abelian simple groups serve as building blocks for all finite groups through composition series.
Key Properties of Abelian Simple Groups
Abelian simple groups are precisely the cyclic groups of prime order, characterized by their commutative operation and lack of nontrivial normal subgroups. These groups exhibit a straightforward structure where every subgroup is normal, distinguishing them from non-abelian simple groups that have more complex, non-commutative structures. The key property of Abelian simple groups lies in their simplicity and commutativity, making them foundational building blocks in group theory.
Structural Features of Non-Abelian Simple Groups
Non-Abelian simple groups are characterized by their lack of nontrivial normal subgroups and a complex internal structure, distinguishing them from Abelian simple groups which are cyclic of prime order. These groups typically exhibit rich symmetry properties and often arise as finite groups of Lie type or alternating groups, reflecting intricate algebraic and geometric features. Their non-commutative operation leads to highly non-trivial conjugacy classes and representation theories essential in modern group theory and theoretical physics.
Classic Examples: Abelian vs Non-Abelian Simple Groups
Classic examples of Abelian simple groups are cyclic groups of prime order, denoted as \( \mathbb{Z}_p \) for a prime \( p \), which exhibit commutative properties and lack proper nontrivial normal subgroups. Non-Abelian simple groups include the alternating groups \( A_n \) for \( n \geq 5 \), characterized by their non-commutative operation and simplicity due to the absence of nontrivial normal subgroups. These distinctions emphasize the fundamental structural differences between Abelian simple groups, which are straightforward and commutative, and the more complex, non-commutative nature of Non-Abelian simple groups.
Historical Significance in Group Theory
Non-abelian simple groups played a pivotal role in the historical development of group theory by providing examples of fundamental building blocks beyond the well-understood Abelian groups, which are commutative. The classification of finite simple groups, completed in the late 20th century, highlighted the complexity and richness of non-abelian simple groups compared to Abelian groups, which are all cyclic of prime order or products thereof. These findings revolutionized the understanding of symmetry and structure in algebra, proving essential for advances in many areas of mathematics and theoretical physics.
Classification of Finite Simple Groups
Non-abelian simple groups play a central role in the Classification of Finite Simple Groups, which asserts that every finite simple group is isomorphic to one of several well-defined families: cyclic groups of prime order (Abelian), alternating groups of degree at least five, simple groups of Lie type, or one of 26 sporadic groups. Abelian simple groups are precisely the cyclic groups of prime order, representing the building blocks of Abelian groups, but lack the complex structures found in non-abelian cases. The classification provides a comprehensive framework distinguishing the fundamental nature and structural complexity between Abelian and non-abelian simple groups within the landscape of finite group theory.
Applications in Mathematics and Physics
Non-abelian simple groups, characterized by their non-commutative operations, play a crucial role in the classification of finite simple groups and the study of symmetry in quantum mechanics. Abelian groups, which have commutative group operations, are fundamental in number theory, algebraic topology, and crystallography due to their straightforward structure and predictability. The distinction between non-abelian simple and abelian groups allows mathematicians and physicists to model complex phenomena such as particle interactions and symmetry breaking in gauge theories.
Major Differences: Abelian Simple vs Non-Abelian Simple
Abelian simple groups consist exclusively of cyclic groups of prime order, characterized by commutative group operations where every element commutes with every other element. In contrast, non-Abelian simple groups exhibit non-commutative properties, with more complex internal structures that prevent element-wise commutation, making them essential in the classification of finite simple groups. The core distinction lies in the Abelian simple groups' straightforward, commutative nature versus the intricate, non-commutative configurations defining non-Abelian simple groups.
Conclusion: The Importance of Simple Groups in Algebra
Non-abelian simple groups play a crucial role in algebra due to their structural complexity and function as building blocks for all finite groups, contrasting with Abelian groups which are commutative and structurally simpler. The classification of finite simple groups, a monumental achievement in mathematics, highlights the importance of non-abelian simple groups in understanding group theory and symmetry. Their study provides deep insights into algebraic structures, demonstrating that simple groups serve as the fundamental components from which more complex groups are constructed.
Non-abelian simple Infographic
 libterm.com
libterm.com