Correlation measures the strength and direction of the relationship between two variables, helping you understand how changes in one variable might predict changes in another. It is often quantified using Pearson's correlation coefficient, which ranges from -1 to 1, indicating negative, no, or positive correlation. Discover how correlation impacts data analysis and decision-making by reading the full article.
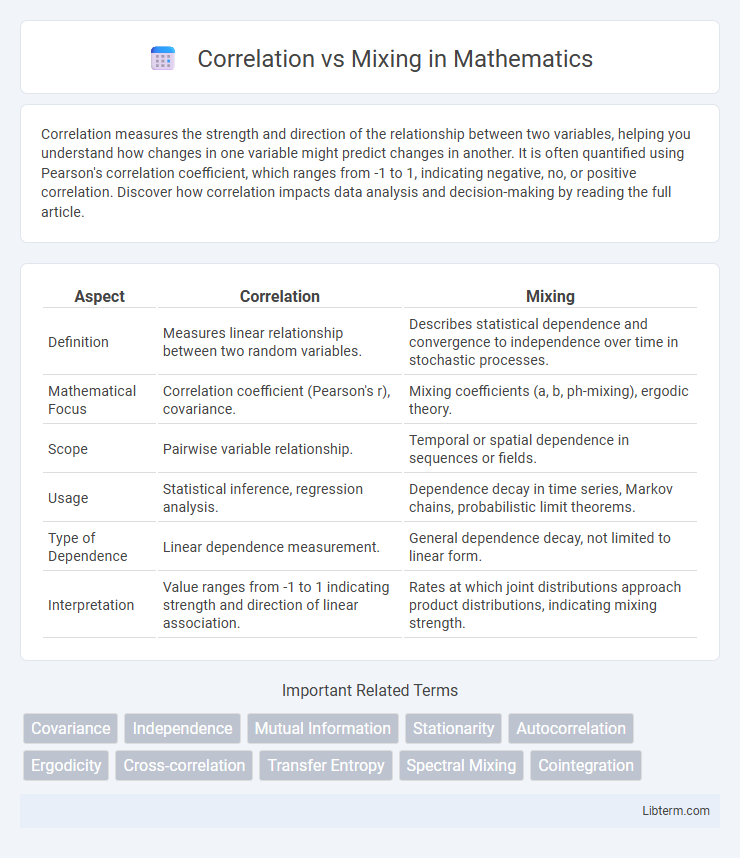
Table of Comparison
| Aspect | Correlation | Mixing |
|---|---|---|
| Definition | Measures linear relationship between two random variables. | Describes statistical dependence and convergence to independence over time in stochastic processes. |
| Mathematical Focus | Correlation coefficient (Pearson's r), covariance. | Mixing coefficients (a, b, ph-mixing), ergodic theory. |
| Scope | Pairwise variable relationship. | Temporal or spatial dependence in sequences or fields. |
| Usage | Statistical inference, regression analysis. | Dependence decay in time series, Markov chains, probabilistic limit theorems. |
| Type of Dependence | Linear dependence measurement. | General dependence decay, not limited to linear form. |
| Interpretation | Value ranges from -1 to 1 indicating strength and direction of linear association. | Rates at which joint distributions approach product distributions, indicating mixing strength. |
Understanding Correlation: Definition and Concepts
Correlation measures the statistical relationship and degree of linear association between two variables, commonly expressed through the correlation coefficient ranging from -1 to 1. Understanding correlation involves concepts such as positive correlation, negative correlation, and zero correlation, which indicate the direction and strength of the relationship. This measure helps in predicting the behavior of one variable based on the other and differentiates from mixing, which refers to combining different substances or signals without implying a statistical relationship.
What is Mixing? Key Principles Explained
Mixing is the process of combining two or more signals or datasets to create a new signal that contains components of the original inputs, often used in audio production and signal processing. Key principles of mixing involve balancing levels, equalizing frequencies, and applying effects to enhance clarity and cohesion of individual elements within the combined output. Understanding time alignment, phase coherence, and frequency spectrum management is essential to achieving a clean, harmonious mix without unwanted distortion or masking.
Fundamental Differences Between Correlation and Mixing
Correlation measures the statistical relationship and dependency between two variables, quantifying how one variable changes in connection with another. Mixing describes the process by which a system evolves over time toward a state of statistical independence, losing memory of its initial conditions and ensuring past and future events become increasingly uncorrelated. Fundamentally, correlation captures instantaneous or static associations, while mixing characterizes dynamic convergence to equilibrium and decay of dependence in stochastic or dynamical systems.
Real-World Applications: Correlation in Data Analysis
Correlation measures the strength and direction of a linear relationship between two variables, playing a crucial role in real-world data analysis such as finance, healthcare, and social sciences. Analysts use correlation coefficients to identify trends, make predictions, and assess risk, enabling data-driven decision-making across industries. Unlike mixing, which pertains to dependency decay over time in stochastic processes, correlation specifically targets pairwise variable relationships in static datasets.
Mixing in Practice: Examples Across Industries
Mixing in practice involves combining diverse audio tracks or signals to create a cohesive final product, essential in music production, film sound design, and broadcasting. Industries such as music production use mixing to balance vocals and instruments for clarity and emotional impact, while film post-production relies on it to integrate dialogue, sound effects, and music seamlessly. In broadcasting, mixing ensures consistent audio levels and quality across live and recorded content, enhancing listener experience and engagement.
Interdependence vs. Randomness: Core Distinctions
Correlation measures the degree of interdependence between variables, indicating how changes in one variable systematically relate to changes in another. Mixing describes the process by which a system loses memory of its initial state, exemplifying randomness through statistical independence over time or space. Understanding the core distinction emphasizes that correlation captures predictable relationships, while mixing reflects the emergence of randomness and loss of structure in complex systems.
Mathematical Approaches to Correlation and Mixing
Mathematical approaches to correlation involve statistical measures such as Pearson's correlation coefficient, which quantifies the linear relationship between two variables, and Spearman's rank correlation for monotonic relationships. Mixing in mathematical contexts refers to the analysis of how different signals or probability distributions combine, often modeled through convolution or mixing matrices to represent composite effects. Both frameworks utilize matrix algebra and integral transforms to rigorously describe dependencies and blending phenomena in multivariate systems.
Statistical Implications of Correlation and Mixing
Correlation measures the linear relationship between variables, directly influencing the predictability and interpretability of statistical models. Mixing refers to the dependence decay property in stochastic processes, ensuring that distant observations become nearly independent, which is crucial for validating asymptotic results like the law of large numbers and central limit theorems. Understanding the statistical implications of correlation and mixing is essential for accurate inference, as high correlation can bias estimates while strong mixing conditions guarantee the consistency and efficiency of estimators in time series and spatial data analysis.
Challenges in Distinguishing Correlation from Mixing
Distinguishing correlation from mixing presents significant challenges due to overlapping statistical signals where correlated variables may appear mixed in complex datasets. Noise and hidden confounding factors often obscure the true sources of observed correlations, complicating the identification of independent components. Advanced techniques such as Independent Component Analysis (ICA) and Partial Correlation Analysis are necessary to accurately separate genuine correlations from mixing effects in multidimensional data.
Conclusion: Choosing the Right Approach for Your Data
Correlation measures the statistical relationship and linear dependence between variables, making it ideal for identifying direct associations in data sets. Mixing involves combining different data sources or distributions to create a new, composite dataset, useful for enhancing diversity or complexity in analysis. Selecting the appropriate method depends on the analysis goal: use correlation for uncovering relationships and mixing for generating richer or more nuanced data representations.
Correlation Infographic
 libterm.com
libterm.com