A positive measure refers to a mathematical concept where a measure assigns a non-negative value to sets within a measurable space, ensuring consistency and meaningful interpretation in probability and analysis. This property guarantees that the measure accurately reflects the size or probability of events without negative values, which aligns with intuition and real-world applications. Explore the rest of the article to deepen your understanding of positive measures and their significance in various mathematical contexts.
Table of Comparison
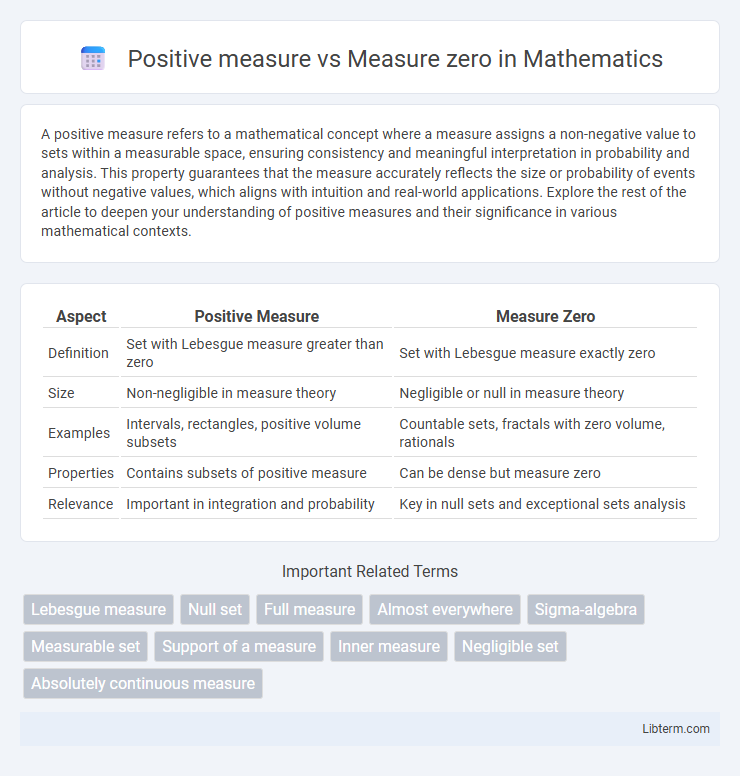
| Aspect | Positive Measure | Measure Zero |
|---|---|---|
| Definition | Set with Lebesgue measure greater than zero | Set with Lebesgue measure exactly zero |
| Size | Non-negligible in measure theory | Negligible or null in measure theory |
| Examples | Intervals, rectangles, positive volume subsets | Countable sets, fractals with zero volume, rationals |
| Properties | Contains subsets of positive measure | Can be dense but measure zero |
| Relevance | Important in integration and probability | Key in null sets and exceptional sets analysis |
Understanding Measure Theory: Key Concepts
Positive measure refers to a set in measure theory that has a strictly greater than zero measure, indicating the presence of "mass" or "size" in the given space. Measure zero, on the other hand, describes sets that are negligible or "small" in terms of measure, meaning their measure is exactly zero despite possibly containing infinitely many points. Understanding these concepts is fundamental in measure theory, as it distinguishes between sets that effectively contribute to integration and probability calculations and those that do not.
Defining Positive Measure and Measure Zero
Positive measure refers to a set in a measure space that has a strictly greater than zero measure, indicating it occupies a non-negligible portion of the space. Measure zero, or null set, is a set whose measure equals zero, implying it is negligible or negligible in size within the context of the measure. These definitions are fundamental in measure theory, where positive measure sets are often associated with significant subsets, while measure zero sets can be disregarded for many analytical purposes.
Mathematical Foundations: Lebesgue Measure Explained
In measure theory, a set with positive measure has a Lebesgue measure greater than zero, indicating it occupies a non-negligible volume in the real number space. Conversely, a measure zero set, also called a null set, has Lebesgue measure zero and can be covered by intervals of arbitrarily small total length, signifying it is negligible in size. Understanding these concepts is fundamental for integration, probability, and functional analysis within the mathematical foundations of Lebesgue measure.
Properties of Sets with Measure Zero
Sets with measure zero are characterized by their ability to be covered by countably many intervals whose total length can be made arbitrarily small, indicating negligible "size" in terms of Lebesgue measure. They have no interior points and are nowhere dense, meaning they cannot contain any interval of positive length, distinguishing them sharply from sets of positive measure. These properties imply that functions defined on measure zero sets typically do not affect integrals, highlighting their fundamental role in measure theory and real analysis.
Examples of Positive Measure in Real-World Contexts
Positive measure sets in real-world contexts often include intervals on the number line such as the length of a road segment or time duration between events, both quantifiable by Lebesgue measure greater than zero. For instance, a lake's surface area detected via satellite imagery represents a set with positive two-dimensional Lebesgue measure, distinguishing it from thin fractal-like coastlines of measure zero. In signal processing, sound waves over a time interval demonstrate positive Lebesgue measure in the time domain, contrasting against singular points where signals vanish, which have measure zero.
Distinguishing Measure Zero from Empty Sets
Measure zero sets contain points with negligible "size" in terms of Lebesgue measure but can still be infinite or uncountable, unlike empty sets which contain no points at all. Positive measure sets have a strictly positive Lebesgue measure, indicating a "volume" greater than zero, distinguishing them sharply from measure zero sets. Understanding this distinction is crucial in real analysis and measure theory for classifying sets based on their size and measure properties.
Importance in Integration and Probability Theory
Positive measure sets represent regions with nonzero "size" or probability, crucial in integration where integrals over these sets yield meaningful values. Measure zero sets, despite possibly being infinite or dense, contribute nothing to Lebesgue integrals and do not affect probability distributions. Understanding the distinction emphasizes which events or function domains impact integral calculations and probabilistic outcomes, ensuring accurate mathematical and statistical analysis.
Applications of Positive Measure in Analysis
Positive measure sets play a critical role in real analysis, particularly in integration theory and probability, where they ensure non-trivial contributions to integrals and expectations. These sets allow the construction of measurable functions with meaningful behavior, enabling the application of Lebesgue integration and Fourier analysis techniques. In contrast, measure zero sets often represent negligible exceptions that do not affect properties such as convergence or differentiability in almost everywhere contexts.
Implications of Measure Zero in Mathematics
Measure zero sets play a crucial role in analysis and probability theory, as they describe collections of points that are negligible in terms of length, area, or volume within a given space. These sets, having Lebesgue measure zero, imply no contribution to integral values or probability measures, thereby simplifying function behavior almost everywhere. Understanding measure zero aids in identifying null sets where properties like continuity or differentiability may fail without affecting the overall mathematical structure.
Summary: Comparing Positive Measure and Measure Zero
Positive measure refers to sets in a measure space whose measure is greater than zero, indicating they occupy a significant "volume" or size within that space. Measure zero sets are collections with no measurable "volume," often negligible in analysis, although they can still be uncountably infinite, like the Cantor set. Understanding the distinction between positive measure and measure zero is fundamental in fields such as real analysis, probability theory, and ergodic theory, where it affects convergence, integration, and the typical behavior of functions.
Positive measure Infographic
 libterm.com
libterm.com