Lebesgue measure is a fundamental concept in real analysis that provides a way to assign a consistent size to subsets of n-dimensional Euclidean space, extending the notion of length, area, and volume beyond simple geometric shapes. It plays a crucial role in integration theory, enabling the integration of more complex functions than traditional Riemann integrals allow. Explore the rest of the article to understand how Lebesgue measure can enhance Your grasp of mathematical analysis.
Table of Comparison
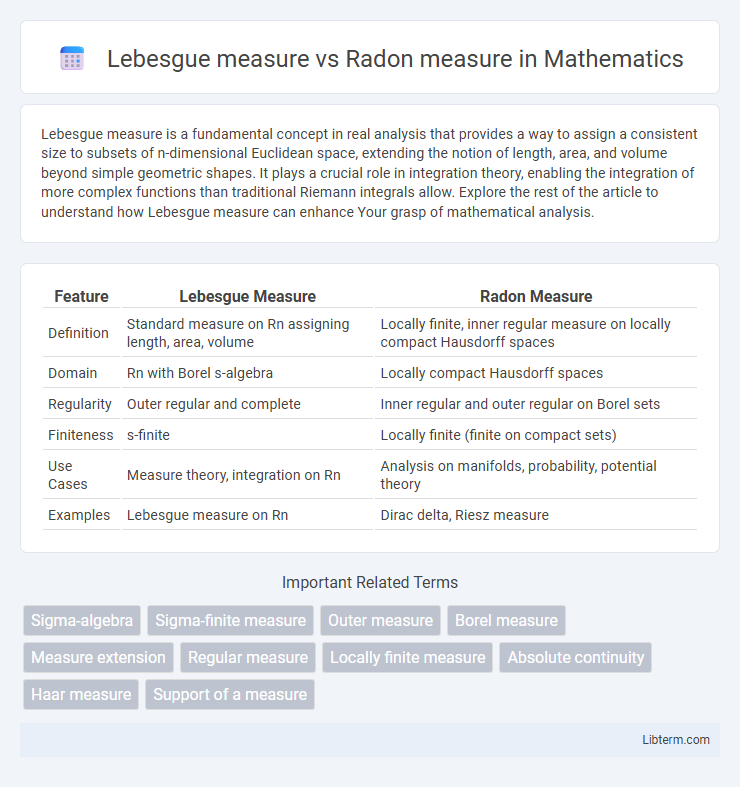
| Feature | Lebesgue Measure | Radon Measure |
|---|---|---|
| Definition | Standard measure on Rn assigning length, area, volume | Locally finite, inner regular measure on locally compact Hausdorff spaces |
| Domain | Rn with Borel s-algebra | Locally compact Hausdorff spaces |
| Regularity | Outer regular and complete | Inner regular and outer regular on Borel sets |
| Finiteness | s-finite | Locally finite (finite on compact sets) |
| Use Cases | Measure theory, integration on Rn | Analysis on manifolds, probability, potential theory |
| Examples | Lebesgue measure on Rn | Dirac delta, Riesz measure |
Introduction to Measure Theory
Lebesgue measure is a fundamental example of a complete measure defined on the sigma-algebra of Lebesgue measurable sets in Euclidean space, central to integration and probability theory. Radon measures generalize this concept by being locally finite and inner regular, defined on the Borel sigma-algebra of locally compact Hausdorff spaces, thus extending measure theory to more abstract topological settings. Both measures provide crucial frameworks in measure theory, with Lebesgue measure emphasizing completeness and translation invariance, while Radon measures enable finer analysis on diverse spaces through their regularity properties.
Defining Lebesgue Measure
The Lebesgue measure is defined on the sigma-algebra of Lebesgue measurable sets in Euclidean space, assigning lengths, areas, or volumes consistent with our intuitive notion of size. It extends the idea of length from intervals to more complex sets by using outer measures and Caratheodory's criterion to ensure countable additivity and completeness. Compared to Radon measures, Lebesgue measure specifically quantifies subsets of R^n with properties such as translation invariance and sigma-finiteness, making it fundamental in real analysis and probability theory.
Understanding Radon Measure
Radon measures generalize Lebesgue measures by allowing the assignment of measures to more complex topological spaces, including locally compact Hausdorff spaces, rather than just subsets of Euclidean space. They are defined as locally finite Borel measures that are inner regular, meaning the measure of any set can be approximated from within by compact sets, which enhances their applicability in functional analysis and probability theory. Unlike Lebesgue measures, Radon measures can effectively handle measures on curved or non-Euclidean domains, facilitating advanced integration and measure-theoretic frameworks.
Key Properties of Lebesgue Measure
Lebesgue measure is a complete, translation-invariant measure defined on the s-algebra of Lebesgue measurable subsets of \(\mathbb{R}^n\), assigning standard length, area, or volume consistent with intuitive geometric size. It is s-finite and countably additive, ensuring measurable sets can be approximated well by open or closed sets, critical for integration theory. In contrast, Radon measures generalize Lebesgue measures on locally compact Hausdorff spaces, allowing inner regularity and local finiteness without requiring translation invariance.
Fundamental Characteristics of Radon Measure
Radon measures are defined on locally compact Hausdorff spaces and uniquely combine inner regularity on open sets with outer regularity on all Borel sets, distinguishing them from Lebesgue measures which primarily apply to Euclidean spaces. Unlike Lebesgue measures, Radon measures are finite on compact sets, making them well-suited for analysis on general topological spaces. Their strong regularity properties and compatibility with continuous functions ensure a robust framework for integration and convergence theorems beyond standard Lebesgue theory.
Differences Between Lebesgue and Radon Measures
The Lebesgue measure is defined specifically on the sigma-algebra of Lebesgue measurable sets in Euclidean space, providing a complete measure that generalizes length, area, and volume. Radon measures extend this concept to locally finite Borel measures on locally compact Hausdorff spaces, allowing integration against continuous functions with compact support. Unlike the Lebesgue measure, Radon measures are more flexible in topological spaces beyond Euclidean settings and can assign finite measure to all compact sets, enabling broader applications in functional analysis and probability theory.
Applications of Lebesgue Measure
Lebesgue measure is fundamental in real analysis and probability theory, providing a rigorous framework for integration and measurable functions on Euclidean spaces. It enables precise evaluation of volume, area, and length, essential in defining integrals in probability, statistics, and partial differential equations. Applications extend to functional analysis, where Lebesgue measure supports the development of Lp spaces and Fourier analysis, critical in signal processing and quantum mechanics.
Applications of Radon Measure
Radon measures are widely used in functional analysis and probability theory due to their ability to assign measures to more general topological spaces than Lebesgue measures, which are restricted to Euclidean spaces. Applications of Radon measures include characterizing distributions in infinite-dimensional spaces and providing a framework for integrating functions with respect to measures on locally compact Hausdorff spaces. These properties make Radon measures essential in areas such as stochastic processes, potential theory, and the study of partial differential equations.
Relationships and Extensions: Lebesgue Vs. Radon
Lebesgue measure is a specific instance of a Radon measure defined on the Euclidean space, primarily focusing on assigning volume to subsets of \(\mathbb{R}^n\). Radon measures generalize Lebesgue measure by extending to locally compact Hausdorff spaces, allowing for more flexible integration and measure theory applications beyond Lebesgue's scope. The Radon measure framework encompasses Lebesgue measure while supporting measures that are finite on compact sets and inner regular, making it essential for advanced functional analysis and probability theory.
Conclusion: Choosing the Appropriate Measure
Selecting between Lebesgue and Radon measures depends on the context of application and the properties required. Lebesgue measure excels in standard analysis on Euclidean spaces due to its completeness and translation invariance, making it ideal for integrals of real-valued functions. Radon measure offers greater flexibility on locally compact Hausdorff spaces, supporting regularity and finite measure on compact sets, thus suited for advanced applications in functional analysis and probability theory.
Lebesgue measure Infographic
 libterm.com
libterm.com