Tangent space is a fundamental concept in differential geometry representing a linear approximation of a manifold at a given point, capturing directions in which one can tangentially move. It plays a crucial role in fields such as physics and computer graphics by enabling complex surface analysis and transformations. Explore the rest of this article to deepen your understanding of tangent spaces and their practical applications.
Table of Comparison
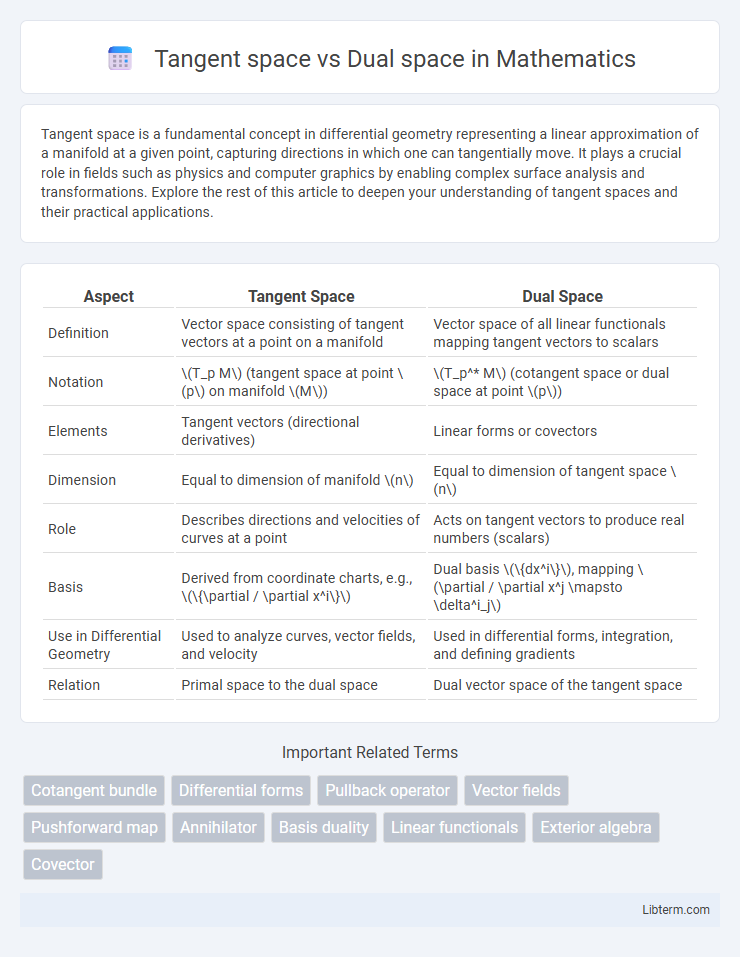
| Aspect | Tangent Space | Dual Space |
|---|---|---|
| Definition | Vector space consisting of tangent vectors at a point on a manifold | Vector space of all linear functionals mapping tangent vectors to scalars |
| Notation | \(T_p M\) (tangent space at point \(p\) on manifold \(M\)) | \(T_p^* M\) (cotangent space or dual space at point \(p\)) |
| Elements | Tangent vectors (directional derivatives) | Linear forms or covectors |
| Dimension | Equal to dimension of manifold \(n\) | Equal to dimension of tangent space \(n\) |
| Role | Describes directions and velocities of curves at a point | Acts on tangent vectors to produce real numbers (scalars) |
| Basis | Derived from coordinate charts, e.g., \(\{\partial / \partial x^i\}\) | Dual basis \(\{dx^i\}\), mapping \(\partial / \partial x^j \mapsto \delta^i_j\) |
| Use in Differential Geometry | Used to analyze curves, vector fields, and velocity | Used in differential forms, integration, and defining gradients |
| Relation | Primal space to the dual space | Dual vector space of the tangent space |
Introduction to Tangent Space and Dual Space
Tangent space at a point on a differentiable manifold consists of all possible velocity vectors of curves passing through that point, capturing directional derivatives and local linear approximations. Dual space, also known as the cotangent space, is the vector space of all linear functionals acting on the tangent space, mapping tangent vectors to real numbers. These spaces play fundamental roles in differential geometry, enabling the formulation of differential forms and vector fields essential for manifold analysis.
Defining the Tangent Space
The tangent space at a point on a differentiable manifold is a vector space consisting of all possible velocity vectors of curves passing through that point, formalized as derivations acting on smooth functions. This space captures the notion of directional derivatives and linearizes the manifold locally, providing a framework for analyzing vector fields and differential equations. In contrast, the dual space comprises linear functionals mapping tangent vectors to real numbers, enabling the study of covectors and differential forms.
Understanding the Dual Space
The dual space of a vector space V consists of all linear functionals mapping vectors in V to scalars, providing a framework to analyze vector spaces through their linear evaluations. Unlike the tangent space, which contains vectors representing directions at a point on a manifold, the dual space captures the space of covectors or linear maps acting on those tangent vectors. Understanding the dual space is essential in differential geometry and physics for formulating concepts like gradients, differential forms, and covariant derivatives.
Mathematical Structure of Tangent Spaces
Tangent spaces consist of vectors that represent directional derivatives at a point on a differentiable manifold, forming a vector space isomorphic to Rn for an n-dimensional manifold. The mathematical structure of tangent spaces enables the definition of differentiation on manifolds by capturing infinitesimal displacements along curves. Unlike dual spaces, which consist of linear functionals acting on tangent vectors, tangent spaces provide the foundational geometric framework necessary for the local analysis of manifolds and their differentiable mappings.
Properties and Basis of Dual Spaces
The tangent space at a point on a differentiable manifold consists of all possible directional derivatives or velocity vectors that originate at that point, forming a vector space defined by coordinate basis vectors. The dual space, known as the cotangent space, is the vector space of all linear functionals mapping vectors from the tangent space to real numbers, characterized by dual basis covectors that satisfy the Kronecker delta identity with the tangent basis vectors. The dual basis is uniquely determined by its bi-orthogonality property: each covector acts as a projection extracting the corresponding component of a tangent vector, making the dual space fundamental in defining differential forms and facilitating coordinate-independent tensor analysis.
Relationship Between Tangent and Dual Spaces
The tangent space at a point on a manifold consists of all tangent vectors representing possible directions in which one can move from that point, whereas the dual space contains all linear functionals that map these tangent vectors to real numbers. The relationship between tangent and dual spaces is characterized by the natural pairing, where each element of the dual space acts as a linear map on the tangent space, reflecting concepts such as gradients acting on directional derivatives. This duality underpins many fundamental constructions in differential geometry, including the definition of differential forms and the cotangent bundle.
Coordinate Representation: Tangent Vectors vs. Covectors
Tangent space at a point on a manifold consists of tangent vectors represented by directional derivatives or velocity vectors in coordinate bases, typically denoted as partial derivatives with respect to coordinates. Dual space, or cotangent space, contains covectors that act as linear functionals on tangent vectors, often expressed as differentials of coordinate functions. The coordinate representation distinguishes tangent vectors as column vectors transforming with the Jacobian matrix, while covectors transform contravariantly as row vectors multiplied by the inverse Jacobian matrix.
Applications in Differential Geometry and Physics
Tangent space, fundamental in differential geometry, represents all possible directions in which one can tangentially pass through a point on a manifold, enabling analysis of curves, surfaces, and vector fields. Dual space, composed of linear functionals mapping tangent vectors to real numbers, plays a critical role in formulating differential forms and covectors, essential for integration on manifolds and defining physical quantities like momentum and force in physics. Applications in general relativity utilize tangent spaces to describe velocity and acceleration, while dual spaces facilitate the formulation of Einstein's field equations through stress-energy tensors and differential forms.
Examples Illustrating Tangent and Dual Spaces
Tangent spaces at a point on a manifold represent all possible velocity vectors of curves passing through that point, such as vectors tangent to a sphere's surface in differential geometry. Dual spaces consist of linear functionals mapping tangent vectors to real numbers, exemplified by differential forms assigning real values to tangent vectors on surfaces. For instance, on a 2D surface, the tangent space includes vectors like directional derivatives, while the dual space contains gradient covectors evaluating these directions.
Summary: Key Differences and Insights
Tangent space at a point on a manifold consists of all possible velocity vectors of curves passing through that point, representing directions for movement within the manifold. Dual space, also called the cotangent space, comprises linear functionals mapping vectors from the tangent space to real numbers, serving as tools for measuring or evaluating vectors. The key difference lies in their roles: tangent spaces describe directional derivatives and geometric vectors, while dual spaces provide covectors used in differential forms and gradients.
Tangent space Infographic
 libterm.com
libterm.com