Fuzzy measure is a mathematical concept used to quantify uncertainty and partial truth in various decision-making processes, extending traditional measures by allowing overlapping and non-additive values. This tool is essential in fields like artificial intelligence, data fusion, and information retrieval for modeling complex systems where classical probability falls short. Explore the rest of the article to understand how fuzzy measures improve your analysis and decision-making strategies.
Table of Comparison
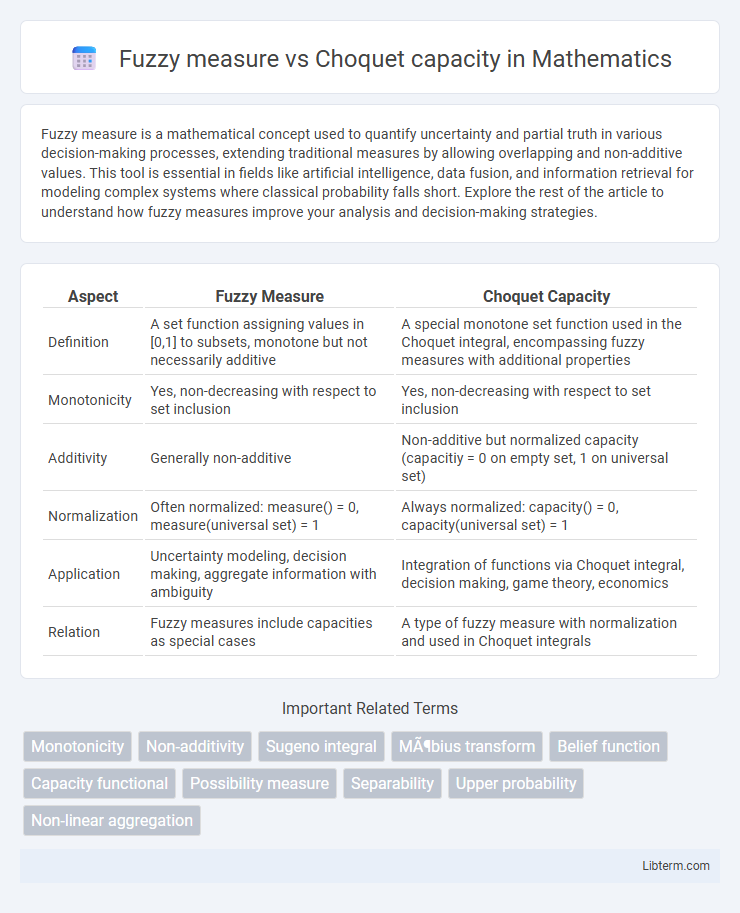
| Aspect | Fuzzy Measure | Choquet Capacity |
|---|---|---|
| Definition | A set function assigning values in [0,1] to subsets, monotone but not necessarily additive | A special monotone set function used in the Choquet integral, encompassing fuzzy measures with additional properties |
| Monotonicity | Yes, non-decreasing with respect to set inclusion | Yes, non-decreasing with respect to set inclusion |
| Additivity | Generally non-additive | Non-additive but normalized capacity (capacitiy = 0 on empty set, 1 on universal set) |
| Normalization | Often normalized: measure() = 0, measure(universal set) = 1 | Always normalized: capacity() = 0, capacity(universal set) = 1 |
| Application | Uncertainty modeling, decision making, aggregate information with ambiguity | Integration of functions via Choquet integral, decision making, game theory, economics |
| Relation | Fuzzy measures include capacities as special cases | A type of fuzzy measure with normalization and used in Choquet integrals |
Introduction to Fuzzy Measures
Fuzzy measures generalize classical measures by relaxing additivity to monotonicity, allowing for more flexible modeling of uncertainty in diverse systems. Choquet capacity is a specific type of fuzzy measure that emphasizes set functions satisfying boundary conditions and monotonicity, enabling the representation of interaction among elements in a set. These measures play a crucial role in fields like decision theory, information aggregation, and artificial intelligence for handling imprecise or subjective data.
Concept and Definition of Choquet Capacity
Choquet capacity is a specific type of fuzzy measure characterized by monotonicity, where the measure of a set never exceeds the measure of its supersets, reflecting a non-additive probability framework. Unlike general fuzzy measures, Choquet capacities ensure that the measure of the empty set is zero and the measure of the entire set is one, aligning with normalized set functions. This concept plays a critical role in decision theory and aggregation operators by capturing interaction among criteria through non-linear aggregation.
Mathematical Foundations: Fuzzy Measure vs Choquet Capacity
Fuzzy measures generalize classical measures by allowing non-additivity, capturing uncertainty and interaction among elements through monotone set functions defined on a sigma-algebra. Choquet capacity is a specialized type of fuzzy measure characterized by monotonicity and normalization conditions, often used in decision theory and game theory to model capacities with orderings but without full additivity. Both concepts share mathematical foundations in measure theory, but Choquet capacities emphasize capacity functions that facilitate integral representations and aggregation operators.
Key Properties and Axioms
Fuzzy measures and Choquet capacities both generalize traditional measures by allowing non-additivity, but differ in key axiomatic properties. Fuzzy measures require monotonicity, ensuring that the measure of a set is always less than or equal to that of its superset, while Choquet capacities add normalization conditions, assigning zero to the empty set and one to the entire space. Both frameworks emphasize monotonicity, but Choquet capacities mandate boundary conditions that are crucial for defining the Choquet integral in aggregation problems.
Representation Theorems and Similarities
Fuzzy measures and Choquet capacities both rely on monotone set functions to model uncertainty and interaction among elements, with representation theorems emphasizing their equivalence under specific conditions. Each framework can be characterized through the Mobius transform, enabling an explicit decomposition of the measure into contributions from individual and combined subsets. Similarities arise in their use within decision theory and aggregation operators, where Choquet capacities often serve as generalized fuzzy measures supporting non-additive integration.
Major Differences Between Fuzzy Measure and Choquet Capacity
Fuzzy measures and Choquet capacities both assign values to subsets of a given set, but the major difference lies in their properties; fuzzy measures require only monotonicity, meaning the measure of a set does not decrease when adding elements, whereas Choquet capacities are normalized fuzzy measures with boundary conditions that the measure of the empty set is zero and the measure of the entire set is one. Fuzzy measures can be non-additive and do not necessarily satisfy normalization, while Choquet capacities enforce these conditions to facilitate integration, particularly in decision-making and aggregation contexts. The Choquet integral is defined specifically with respect to a Choquet capacity, making it a more structured approach to handling uncertainty compared to the more general fuzzy measure framework.
Applications in Decision Theory and Uncertainty Modeling
Fuzzy measures and Choquet capacities are fundamental in decision theory for modeling uncertainty and preference aggregation, enabling more flexible representation of interactions among criteria than traditional additive measures. Choquet capacities extend fuzzy measures by satisfying monotonicity, allowing the integration of marginal contributions across subsets in multi-criteria decision-making and risk assessment. These tools enhance uncertainty modeling by capturing non-linear dependencies and subjective judgments within complex systems, improving robustness in scenarios like financial risk, environmental assessment, and artificial intelligence.
Advantages and Limitations of Each Approach
Fuzzy measures offer flexible modeling of uncertainty by capturing interactions among elements without requiring additivity, making them suitable for complex decision-making scenarios, but their computational complexity and lack of standard parameterization can hinder practical implementation. Choquet capacities, a subclass of fuzzy measures characterized by monotonicity, provide a mathematically rigorous framework for aggregation and allow for meaningful interpretations in game theory and decision analysis, yet they may impose restrictive conditions limiting their expressiveness for certain types of uncertainty. Both approaches excel in different contexts: fuzzy measures provide broader modeling capabilities, while Choquet capacities ensure consistency and theoretical tractability.
Comparative Case Studies and Examples
Fuzzy measures and Choquet capacities, while often used interchangeably, differ notably in their mathematical properties and applications within comparative case studies. Fuzzy measures allow for non-additive set functions useful in decision-making scenarios with uncertainty, whereas Choquet capacities specifically satisfy monotonicity, enabling integration in the Choquet integral for modeling interaction among criteria. Case studies in areas like risk assessment and multi-criteria decision analysis demonstrate that Choquet capacities provide more structured aggregation, improving interpretability and consistency over general fuzzy measures.
Future Directions in Fuzzy and Capacity Theory
Future directions in fuzzy measure and Choquet capacity theory emphasize enhanced integration with machine learning algorithms to improve decision-making under uncertainty. Research is advancing toward developing adaptive fuzzy measures capable of dynamically reflecting complex, real-world interactions in big data environments. Expanding the theoretical framework of Choquet capacities aims to optimize modeling in areas like artificial intelligence, risk assessment, and multi-criteria analysis.
Fuzzy measure Infographic
 libterm.com
libterm.com