Exterior product, also known as the wedge product, is a crucial operation in linear algebra and differential geometry used to combine vectors into higher-dimensional entities called multivectors. It helps describe oriented areas, volumes, and other geometric concepts by producing antisymmetric results that capture the essence of direction and magnitude. Discover how understanding the exterior product can enhance your grasp of advanced mathematics by reading the full article.
Table of Comparison
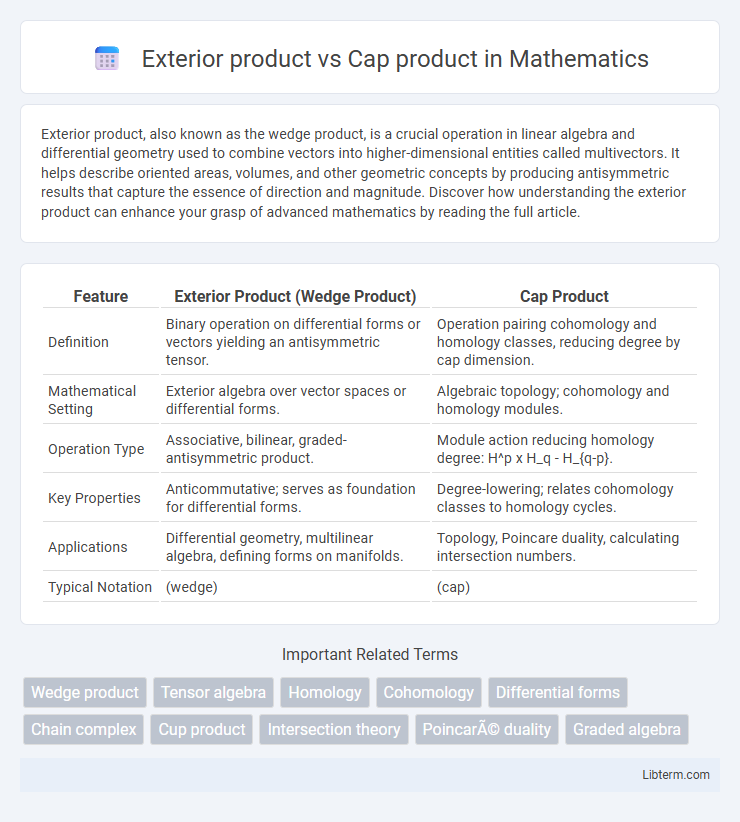
| Feature | Exterior Product (Wedge Product) | Cap Product |
|---|---|---|
| Definition | Binary operation on differential forms or vectors yielding an antisymmetric tensor. | Operation pairing cohomology and homology classes, reducing degree by cap dimension. |
| Mathematical Setting | Exterior algebra over vector spaces or differential forms. | Algebraic topology; cohomology and homology modules. |
| Operation Type | Associative, bilinear, graded-antisymmetric product. | Module action reducing homology degree: H^p x H_q - H_{q-p}. |
| Key Properties | Anticommutative; serves as foundation for differential forms. | Degree-lowering; relates cohomology classes to homology cycles. |
| Applications | Differential geometry, multilinear algebra, defining forms on manifolds. | Topology, Poincare duality, calculating intersection numbers. |
| Typical Notation | (wedge) | (cap) |
Introduction to Exterior vs Cap Products
The exterior product, also known as the wedge product, is an operation in algebraic topology and differential geometry that combines elements of a vector space or differential forms to produce higher-degree forms, playing a crucial role in defining orientations and volumes. The cap product provides a dual operation linking cohomology and homology classes by pairing cochains with chains to yield lower-dimensional homology classes, facilitating the interaction between homology and cohomology theories. Understanding the distinction between the exterior product and cap product is fundamental for applications in multilinear algebra, algebraic topology, and differential geometry, especially in computations involving differential forms and topological invariants.
Definition and Key Features of Exterior Products
The exterior product, also known as the wedge product, is a bilinear operation on differential forms that produces a higher-degree form, playing a crucial role in multilinear algebra and differential geometry. It is antisymmetric, meaning the product of two forms changes sign upon swapping the inputs, and it satisfies the property that the wedge of a form with itself is zero. The key features of exterior products include linearity, antisymmetry, and their ability to construct oriented volumes and encode geometric information, distinguishing them from cap products, which involve pairing cohomology and homology classes in algebraic topology.
Definition and Key Features of Cap Products
The exterior product, also known as the wedge product, is an operation in exterior algebra that combines two differential forms to produce a new form, emphasizing antisymmetry and multilinearity. Cap product, by contrast, is an algebraic operation in algebraic topology that pairs a cohomology class with a homology class, resulting in a homology class of lower dimension. Key features of the cap product include its role in Poincare duality, its definition via the action of cochains on chains, and its capability to relate cohomology and homology groups through a natural bilinear pairing.
Material Differences: Exterior vs Cap Products
Exterior products in algebraic topology primarily involve the wedge or exterior algebra on a vector space, creating antisymmetric tensors fundamental in differential forms and multilinear algebra. Cap products combine cohomology and homology classes on a topological space, resulting in a bilinear product that pairs cochains with chains to produce new homology classes. The material difference lies in exterior products structurally building antisymmetric algebraic objects, while cap products function as interaction operations connecting dual algebraic topological invariants.
Durability and Weather Resistance Comparison
The exterior product is designed with materials that enhance durability and offer superior weather resistance, making it ideal for prolonged outdoor exposure and harsh environmental conditions. Cap products typically feature protective coatings that prevent moisture ingress and UV damage but may require more frequent maintenance to sustain their weatherproof qualities. Compared to cap products, exterior products generally provide longer-lasting performance and better resilience against wear caused by temperature fluctuations and moisture.
Aesthetic Appeal: Design Options and Finishes
The exterior product offers a wide range of design options and finishes that enhance aesthetic appeal through customizable textures and colors, ideal for creating visually striking surfaces. In contrast, the cap product provides sleek, polished finishes that emphasize minimalism and refined elegance, suitable for modern architectural styles. Both products allow for tailored aesthetics, yet the exterior product tends to focus on bold, expressive designs while the cap product prioritizes subtle sophistication.
Cost Considerations: Upfront and Long-Term Investment
The exterior product generally requires a higher upfront investment due to specialized materials and complex installation processes, while the cap product tends to have lower initial costs with simpler application methods. Long-term costs for the exterior product may include maintenance and durability benefits that justify the initial expense, whereas cap products might demand more frequent replacements, increasing cumulative costs over time. Evaluating total cost of ownership involves balancing immediate budget constraints against potential longevity and performance savings in both options.
Installation Process and Compatibility
The exterior product installation process typically involves advanced algebraic topology frameworks, requiring chain complexes and cochain complexes to be precisely aligned for accurate tensor operations. Compatibility for exterior products hinges on the underlying vector spaces or modules being free and graded to ensure the wedge product is well-defined and associative. Cap product installations demand a duality pairing setup between homology and cohomology groups, with compatibility reliant on Poincare duality and appropriate orientation on manifolds for unambiguous algebraic intersection interpretations.
Maintenance Requirements and Lifespan
The exterior product typically demands lower maintenance due to its durable materials resistant to weathering and corrosion, extending its lifespan significantly in outdoor applications. In contrast, the cap product often requires more frequent upkeep because it is more susceptible to environmental wear and may degrade faster without proper protection. Understanding these differences helps in selecting the right product based on long-term maintenance efficiency and expected durability.
Choosing the Right Product for Your Project
Choosing the right product between the exterior product and the cap product depends on the algebraic structures and operations involved in your project, as the exterior product primarily combines vectors to form higher-dimensional antisymmetric tensors, while the cap product operates between cohomology and homology classes to produce new homology classes. Projects requiring manipulation of differential forms or antisymmetric multilinear maps benefit from the exterior product, ideal in differential geometry and algebraic topology contexts. For tasks involving interactions between homology and cohomology, such as computing characteristic classes or dualities in topological spaces, the cap product provides the necessary algebraic tools.
Exterior product Infographic
 libterm.com
libterm.com