Total order is a fundamental concept in mathematics and computer science, referring to a binary relation that arranges elements in a linear sequence where every pair of elements is comparable. This property ensures that for any two elements, one must precede the other, enabling clear and consistent sorting or ranking processes. Explore the rest of the article to understand how total order impacts algorithms and data structures in your computing tasks.
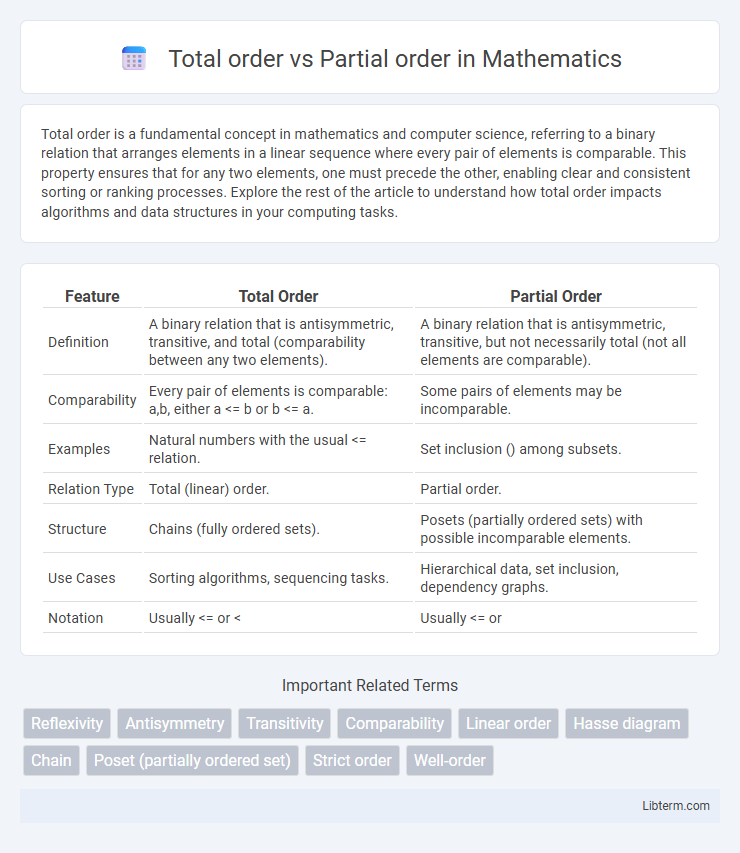
Table of Comparison
| Feature | Total Order | Partial Order |
|---|---|---|
| Definition | A binary relation that is antisymmetric, transitive, and total (comparability between any two elements). | A binary relation that is antisymmetric, transitive, but not necessarily total (not all elements are comparable). |
| Comparability | Every pair of elements is comparable: a,b, either a <= b or b <= a. | Some pairs of elements may be incomparable. |
| Examples | Natural numbers with the usual <= relation. | Set inclusion () among subsets. |
| Relation Type | Total (linear) order. | Partial order. |
| Structure | Chains (fully ordered sets). | Posets (partially ordered sets) with possible incomparable elements. |
| Use Cases | Sorting algorithms, sequencing tasks. | Hierarchical data, set inclusion, dependency graphs. |
| Notation | Usually <= or < | Usually <= or |
Introduction to Order Relations
Order relations define how elements in a set are arranged based on specific properties. A total order ensures every pair of elements is comparable, meaning for any two elements a and b, either a <= b or b <= a holds true. In contrast, a partial order allows some elements to be incomparable, satisfying reflexivity, antisymmetry, and transitivity without requiring total comparability.
Defining Total Order
A total order is a binary relation on a set that is reflexive, antisymmetric, transitive, and total, meaning every pair of elements is comparable. In contrast to partial orders where some elements may be incomparable, total orders ensure a linear sequence where for any two elements \(a\) and \(b\), either \(a \leq b\) or \(b \leq a\). Common examples of total orders include the natural numbers with the usual "less than or equal to" relation.
Defining Partial Order
A partial order is a binary relation over a set that is reflexive, antisymmetric, and transitive, allowing some elements to be incomparable. Unlike total orders, which require every pair of elements to be comparable, partial orders permit the existence of elements without a defined order relation. This structure is crucial in domains such as set theory and computer science for modeling hierarchies and dependencies where not all elements are strictly comparable.
Key Differences Between Total and Partial Order
Total order requires every pair of elements to be comparable, establishing a linear hierarchy, while partial order allows some elements to remain incomparable, forming a more flexible, non-linear structure. In total order, antisymmetry, transitivity, and totality ensure a strict arrangement, whereas partial order only demands antisymmetry and transitivity, lacking the totality condition. Total orders are ideal for sorting and ranking where every element is related, unlike partial orders used in scenarios like subset relationships or task scheduling with dependencies.
Properties of Total Order
Total order is a binary relation on a set that is antisymmetric, transitive, and total, meaning every pair of elements is comparable. This property ensures a linear arrangement where for any two elements a and b, either a <= b or b <= a holds true. In contrast to partial order, total order guarantees no incomparable elements, facilitating straightforward sorting and ranking in mathematical and computer science applications.
Properties of Partial Order
Partial orders are binary relations that are reflexive, antisymmetric, and transitive, allowing elements to be compared only when a specific order relation holds. Unlike total orders, partial orders do not require every pair of elements to be comparable, enabling the representation of more complex hierarchical or dependency structures. This flexibility makes partial orders fundamental in fields like computer science, mathematics, and data organization.
Real-World Examples of Total Order
Total order is exemplified in daily contexts such as ranking athletes by their finishing times in a race, where every competitor's time can be distinctly compared and arranged from fastest to slowest. Another clear example is the chronological ordering of historical events, which follows a linear timeline allowing each event to be placed before or after another without ambiguity. Comparing grades in an academic setting also represents total order, assigning a numeric or letter value to each student that ranks them definitively from highest to lowest performance.
Real-World Examples of Partial Order
Partial orders are common in real-world scenarios such as task scheduling, where certain tasks must precede others without a strict linear sequence. Hierarchies like organizational charts and file directory structures demonstrate partial orders, allowing comparisons only between related elements. Another example is the subset relation among sets, which forms a partial order since not all sets are comparable.
Applications in Computer Science and Mathematics
Total orders are crucial for sorting algorithms, database indexing, and scheduling tasks where all elements must be comparable to enforce a strict sequence. Partial orders underpin dependency resolution, type hierarchies, and graph theory applications, allowing elements to remain incomparable when relationships are not strictly linear. In mathematics, total orders define structures like the real numbers, while partial orders model sets with inherent hierarchical or non-linear relationships such as subsets and divisibility.
Summary: Choosing Between Total and Partial Order
Total order provides a linear arrangement where every pair of elements is comparable, making it ideal for tasks requiring a complete ranking or sequencing. Partial order allows comparison of some elements while others remain incomparable, supporting scenarios involving hierarchical or dependency structures like task scheduling or preference modeling. Selecting between total and partial order depends on the need for comprehensive comparability versus accommodating incomplete or flexible ordering relationships.
Total order Infographic
 libterm.com
libterm.com