A metric space is a set equipped with a function called a metric that defines the distance between any two points within the set, satisfying properties like non-negativity, identity of indiscernibles, symmetry, and the triangle inequality. This structure is fundamental in various branches of mathematics, including analysis, topology, and geometry, as it provides a rigorous way to study concepts like convergence, continuity, and compactness. Explore the rest of the article to deepen your understanding of metric spaces and their applications.
Table of Comparison
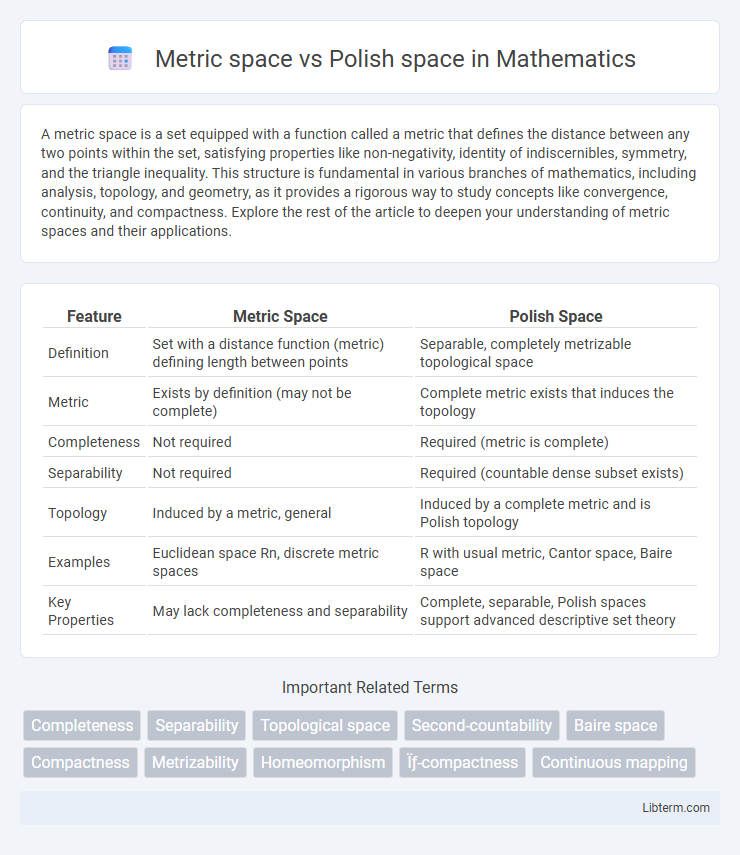
| Feature | Metric Space | Polish Space |
|---|---|---|
| Definition | Set with a distance function (metric) defining length between points | Separable, completely metrizable topological space |
| Metric | Exists by definition (may not be complete) | Complete metric exists that induces the topology |
| Completeness | Not required | Required (metric is complete) |
| Separability | Not required | Required (countable dense subset exists) |
| Topology | Induced by a metric, general | Induced by a complete metric and is Polish topology |
| Examples | Euclidean space Rn, discrete metric spaces | R with usual metric, Cantor space, Baire space |
| Key Properties | May lack completeness and separability | Complete, separable, Polish spaces support advanced descriptive set theory |
Introduction to Metric Spaces
A metric space is a set equipped with a distance function that defines the distance between any two points, satisfying properties such as non-negativity, identity of indiscernibles, symmetry, and the triangle inequality. Polish spaces are a special type of metric space that are complete and separable, meaning they contain a countable dense subset and all Cauchy sequences converge within the space. Understanding metric spaces provides the foundational concepts of convergence, continuity, and compactness essential for studying more advanced structures like Polish spaces.
Key Properties of Metric Spaces
Metric spaces are defined by a distance function (metric) that satisfies positivity, symmetry, the triangle inequality, and identity of indiscernibles, enabling the measurement of distance between any two points. Key properties include completeness, where every Cauchy sequence converges within the space, and separability, characterized by the existence of a countable dense subset. Polish spaces are complete, separable metric spaces distinguished by these properties, making them fundamental in analysis and topology.
Understanding Polish Spaces
Polish spaces are a special class of metric spaces characterized by completeness and separability, meaning they have a countable dense subset and every Cauchy sequence converges within the space. Unlike general metric spaces, which may lack these properties, Polish spaces provide a robust framework for analysis, probability, and descriptive set theory. Key examples of Polish spaces include the real numbers with the standard metric, separable Banach spaces, and spaces of continuous functions, highlighting their importance in advanced mathematical contexts.
Defining Completeness in Metric Spaces
Completeness in metric spaces means every Cauchy sequence converges to a limit within the space, ensuring no "holes" exist. A Polish space is a separable, completely metrizable space, combining completeness with a countable dense subset. Thus, completeness is a key property distinguishing general metric spaces from Polish spaces, which require both completeness and separability.
Separability: A Core Feature of Polish Spaces
Polish spaces are metric spaces distinguished by their separability, meaning they contain a countable dense subset that allows approximation of any point within the space. This separability property ensures that Polish spaces are more manageable for analysis and topology, enabling the application of powerful theorems like the Baire category theorem. In contrast, not all metric spaces are separable, thus lacking the dense countable subset essential for Polish space classification.
Metric Spaces vs Polish Spaces: Core Differences
Metric spaces are sets equipped with a distance function (metric) that defines the distance between any two points, providing the foundation for concepts like convergence and continuity. Polish spaces are a special class of metric spaces characterized by being separable and completely metrizable, meaning they have a countable dense subset and their metric induces a complete topology. The core difference lies in completeness and separability, with Polish spaces requiring both properties, while general metric spaces need only a metric without these additional constraints.
Examples of Metric and Polish Spaces
A metric space is any set equipped with a distance function satisfying non-negativity, identity of indiscernibles, symmetry, and the triangle inequality, such as the real numbers \(\mathbb{R}\) with the usual absolute value metric or \(\mathbb{R}^n\) with the Euclidean distance. Polish spaces are special types of metric spaces that are complete and separable, exemplified by the space of real numbers \(\mathbb{R}\) with the standard metric and the space of continuous functions on \([0,1]\) with the supremum norm. Examples of metric spaces that are not Polish include incomplete spaces like the rational numbers \(\mathbb{Q}\) under the standard metric, which lack completeness.
Applications in Topology and Analysis
Metric spaces provide a foundational framework for convergence, continuity, and compactness in topology and analysis, facilitating the study of geometric properties through distance functions. Polish spaces, as complete separable metric spaces, play a crucial role in descriptive set theory, probability, and functional analysis by enabling advanced measure-theoretic and topological methods. The completeness and separability of Polish spaces ensure robust applications in ergodic theory, dynamical systems, and the characterization of Borel sets beyond general metric space capabilities.
Why Polish Spaces Matter in Mathematics
Polish spaces, defined as complete separable metric spaces, are fundamental in analysis, topology, and probability theory due to their rich structural properties and well-behaved measurable sets. They enable powerful results such as the Borel hierarchy classification, support descriptive set theory, and provide a natural setting for functional analysis and stochastic processes. The completeness and separability conditions in Polish spaces facilitate deep insights into convergence, continuity, and measurability, making them indispensable in modern mathematical research.
Summary: Choosing Between Metric and Polish Spaces
Metric spaces provide a foundational framework in topology defined by a distance function satisfying positivity, symmetry, and the triangle inequality, making them suitable for general analysis and convergence concepts. Polish spaces, a special class of metric spaces that are separable and completely metrizable, offer enhanced structural properties crucial for probability theory, descriptive set theory, and functional analysis. Choosing between metric and Polish spaces depends on the need for completeness and separability; Polish spaces are preferred when working with complex analytic or probabilistic frameworks requiring robust topological structures.
Metric space Infographic
 libterm.com
libterm.com