Context-sensitive languages are a class of formal languages that can be recognized by linear bounded automata and are more powerful than context-free languages. These languages are defined by context-sensitive grammars where production rules depend on the surrounding symbols, allowing for more complex structures. Explore the rest of the article to understand how context-sensitive languages impact computational theory and language processing.
Table of Comparison
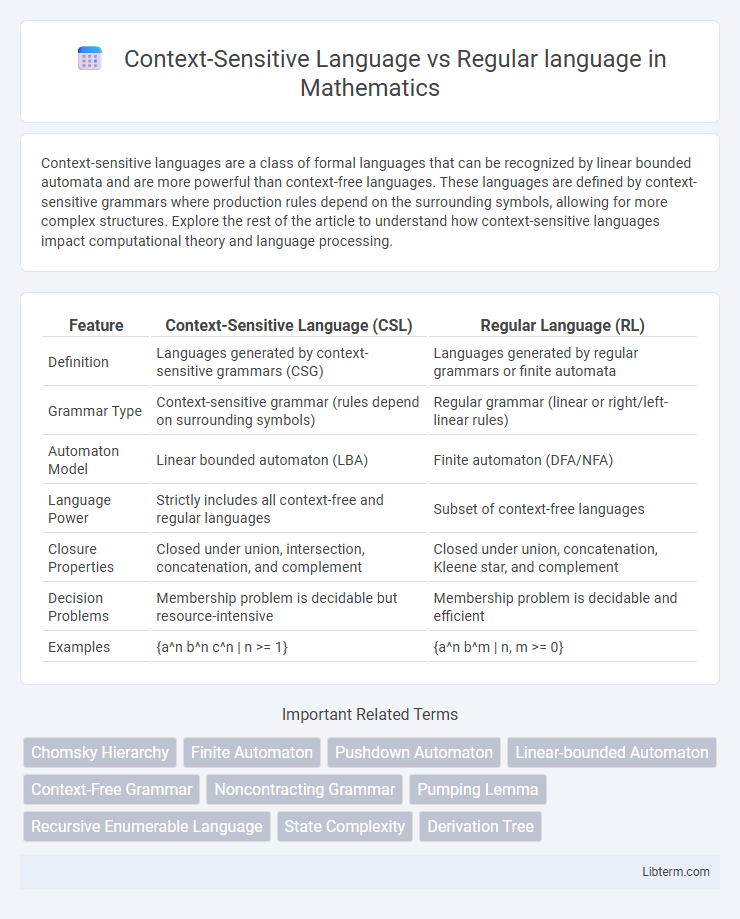
| Feature | Context-Sensitive Language (CSL) | Regular Language (RL) |
|---|---|---|
| Definition | Languages generated by context-sensitive grammars (CSG) | Languages generated by regular grammars or finite automata |
| Grammar Type | Context-sensitive grammar (rules depend on surrounding symbols) | Regular grammar (linear or right/left-linear rules) |
| Automaton Model | Linear bounded automaton (LBA) | Finite automaton (DFA/NFA) |
| Language Power | Strictly includes all context-free and regular languages | Subset of context-free languages |
| Closure Properties | Closed under union, intersection, concatenation, and complement | Closed under union, concatenation, Kleene star, and complement |
| Decision Problems | Membership problem is decidable but resource-intensive | Membership problem is decidable and efficient |
| Examples | {a^n b^n c^n | n >= 1} | {a^n b^m | n, m >= 0} |
Introduction to Formal Languages
Context-sensitive languages (CSLs) are a class of formal languages defined by context-sensitive grammars, where production rules allow substitution based on the surrounding symbols, enabling expression of more complex patterns than regular languages. Regular languages, defined by regular grammars and recognized by finite automata, are limited to simpler structures without memory of context, making them less powerful than CSLs. In formal language theory, CSLs capture a broader range of computational problems and are crucial for understanding the limits of language recognition beyond regular and context-free languages.
Definition of Regular Language
Regular language is defined as a class of languages that can be recognized by finite automata and described by regular expressions, enabling efficient pattern matching and lexical analysis. It is characterized by closure properties under union, concatenation, and Kleene star operations, making it simpler than context-sensitive languages, which require more powerful computational models like linear bounded automata for recognition. Understanding the limitations of regular languages helps in distinguishing them from context-sensitive languages in formal language theory and compiler design.
Definition of Context-Sensitive Language
Context-sensitive languages are a class of formal languages defined by context-sensitive grammars, where production rules are of the form aAb - agb, allowing substitution only when non-terminal A is surrounded by specific contexts a and b. These languages are strictly more powerful than regular languages, which are defined by finite automata and have simpler, context-free production rules. Context-sensitive languages can describe constructs that require context consideration, making them essential in complex language processing and computational linguistics.
Key Differences Between Regular and Context-Sensitive Languages
Regular languages are defined by finite automata and can be described using regular expressions, while context-sensitive languages require linear bounded automata for their recognition and involve more complex grammar rules. Regular languages have a limited computational power and cannot handle nested or recursive structures, whereas context-sensitive languages can express languages with context-dependent syntax and nested dependencies. Key differences include the generative capacity where context-sensitive languages strictly contain regular languages, and the decision problems such as membership testing, which is simpler for regular languages due to their finite state nature.
Examples of Regular Languages
Regular languages include patterns recognizable by finite automata, such as strings over {a, b} with an even number of a's or all strings ending with b. Examples also consist of languages like a* or (ab)*, where repetition and concatenation follow fixed, predictable rules. These patterns contrast with context-sensitive languages, which require more powerful computational models to handle nested and interdependent structures.
Examples of Context-Sensitive Languages
Context-sensitive languages include complex syntactic structures such as the language {a^n b^n c^n | n >= 1}, where the number of a's, b's, and c's must be equal, which cannot be recognized by regular or context-free grammars. Another example is the language {a^n b^n c^n d^n | n >= 1}, requiring simultaneous counting of four different symbols, illustrating the increased generative power of context-sensitive grammars. These languages demonstrate the capacity to enforce global constraints unlike regular languages, which are limited to pattern matching and cannot handle nested or multiple dependencies.
Expressive Power Comparison
Context-sensitive languages possess greater expressive power than regular languages, capable of generating complex patterns and dependencies that regular languages cannot. Regular languages are limited to finite automata and cannot handle nested or recursive structures, whereas context-sensitive languages are recognized by linear bounded automata capable of more computationally demanding syntax. This enhanced expressiveness allows context-sensitive languages to model complex programming language grammars and natural languages beyond the scope of regular languages.
Recognition and Automata Models
Context-sensitive languages are recognized by linear bounded automata (LBA), which operate with memory bounded by the input size, enabling them to handle complex dependencies and context conditions in strings. Regular languages are recognized by finite automata, such as deterministic or nondeterministic finite automata (DFA or NFA), characterized by constant memory and simple state transitions insufficient for nested structures. The key distinction lies in the computational power of their automata; LBAs can process context-sensitive grammatical rules, while finite automata are limited to patterns describable by regular expressions, influencing language recognition capabilities.
Practical Applications
Context-sensitive languages enable modeling complex syntactic structures in natural language processing and programming languages that require nested dependencies beyond regular language capabilities. Regular languages suffice for lexical analysis in compilers, pattern matching, and simple protocol design due to their efficient recognition by finite automata. Practical applications leverage context-sensitive grammars for type checking and memory management in advanced compilers, while regular languages dominate in text search engines and network packet filtering.
Conclusion and Future Perspectives
Context-sensitive languages expand computational power beyond regular languages by enabling the recognition of more complex patterns through context-dependent rules. Future research aims to optimize parsing algorithms for context-sensitive languages, improving efficiency and practical applications in natural language processing and formal verification. Advances in machine learning and automata theory are expected to further bridge gaps between context-sensitive and regular language processing capabilities.
Context-Sensitive Language Infographic
 libterm.com
libterm.com