Linear systems exhibit direct proportionality between input and output, making them predictable and easier to analyze mathematically. These systems follow the principle of superposition, meaning the combined response to multiple inputs is the sum of individual responses. Explore the rest of the article to understand how linear models apply across various scientific and engineering fields.
Table of Comparison
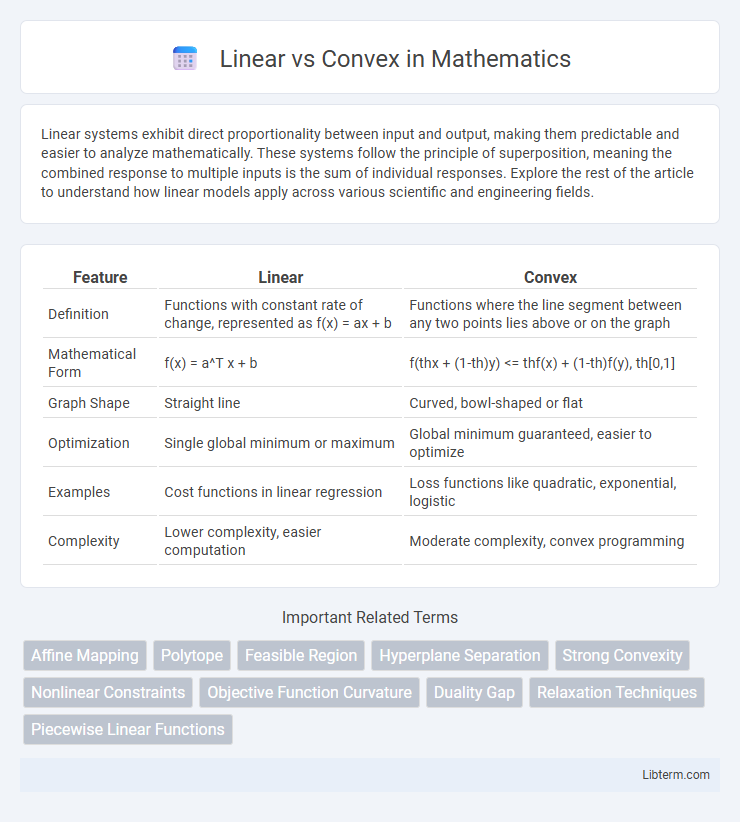
| Feature | Linear | Convex |
|---|---|---|
| Definition | Functions with constant rate of change, represented as f(x) = ax + b | Functions where the line segment between any two points lies above or on the graph |
| Mathematical Form | f(x) = a^T x + b | f(thx + (1-th)y) <= thf(x) + (1-th)f(y), th[0,1] |
| Graph Shape | Straight line | Curved, bowl-shaped or flat |
| Optimization | Single global minimum or maximum | Global minimum guaranteed, easier to optimize |
| Examples | Cost functions in linear regression | Loss functions like quadratic, exponential, logistic |
| Complexity | Lower complexity, easier computation | Moderate complexity, convex programming |
Introduction to Linear and Convex Concepts
Linear concepts involve relationships or functions characterized by constant rates of change and can be represented by straight lines, essential for understanding basic algebra and geometry. Convex concepts extend linearity by incorporating sets and functions where any line segment between two points in the set remains entirely within the set, fundamental for optimization problems and economic modeling. Characterizing problems and solutions through linearity and convexity facilitates efficient algorithm design and ensures global optimality in computational tasks.
Defining Linear Structures
Linear structures are mathematical systems characterized by operations that satisfy additivity and homogeneity, forming the foundation of linear algebra through vector spaces and linear mappings. Convex structures, often studied within convex analysis, are sets where, for any two points, the line segment connecting them lies entirely within the set, emphasizing properties like convex combinations and convex hulls. Defining linear structures involves identifying elements and operations that preserve linearity, such as vector addition and scalar multiplication, distinct from convex structures that focus on the inclusion of all convex combinations.
What Is Convexity?
Convexity refers to the property of a set or function where any line segment connecting two points within the set lies entirely within the set, ensuring no bulges or indentations. In optimization, convex functions have the characteristic that their epigraphs form convex sets, guaranteeing a global minimum exists and can be efficiently found. This contrasts with linear functions, which are flat or straight and lack curvature, making convexity a key concept for understanding the shape and solvability of optimization problems.
Mathematical Representation of Linearity
Linearity in mathematics is represented by equations of the form \(y = mx + b\), where the graph forms a straight line indicating a constant rate of change between variables. Convexity, on the other hand, involves functions where any line segment between two points on the graph lies above or on the curve, typically represented by inequalities such as \(f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda) f(y)\) for \(0 \leq \lambda \leq 1\). While linear functions exhibit additive and homogeneous properties, convex functions emphasize the shape and curvature ensuring that weighted averages do not exceed the function's value at those points.
Mathematical Properties of Convex Sets
Convex sets are defined by the property that for any two points within the set, the entire line segment connecting them lies inside the set, a fundamental characteristic distinguishing them from arbitrary linear sets. Mathematically, convex sets are closed under convex combinations, meaning any weighted average of points in the set remains within the set, which ensures stability in optimization problems. This property leads to important results such as the existence of unique global minima for convex functions defined over convex domains, making convex sets pivotal in mathematical optimization and computational geometry.
Key Differences: Linear vs Convex
Linear functions are characterized by constant rates of change and straight-line graphs, defined by equations of the form f(x) = ax + b. Convex functions, by contrast, have the property that their epigraphs form convex sets, meaning any line segment between two points on the graph lies above or on the graph, often resulting in curved shapes. The key difference lies in linearity implying both convexity and concavity uniformly, whereas convex functions encompass a broader class with curvature that ensures local minima for optimization problems.
Applications in Optimization Problems
Linear optimization problems involve objective functions and constraints represented by linear equations or inequalities, facilitating efficient solutions via methods like the simplex algorithm or interior-point methods. Convex optimization extends these principles to problems where the objective function is convex and constraints form a convex set, ensuring global optimality and applicability in areas such as machine learning, portfolio optimization, and control systems. Convex problems often accommodate nonlinear but structurally favorable functions, enabling robust solutions in diverse applications including signal processing and resource allocation.
Visualization: Linear and Convex in Graphs
Linear functions produce straight lines in graphs with a constant slope, representing a uniform rate of change. Convex functions curve upwards, forming shapes where any line segment between two points on the graph lies above or on the curve, indicating increasing slopes. Visualizing these differences helps in understanding optimization problems, where linear functions suggest simple constraints while convex functions ensure global minima.
Advantages and Limitations of Each
Linear models offer simplicity and interpretability, making them efficient for high-dimensional data and less prone to overfitting. Convex models guarantee global optimality, enhancing solution stability and robustness across various optimization problems. However, linear models may struggle with complex, nonlinear patterns, while convex models can be computationally intensive for large-scale datasets and require careful formulation to maintain convexity.
Choosing Between Linear and Convex Approaches
Choosing between linear and convex approaches depends on the problem's complexity and solution requirements. Linear models excel in simplicity and computational efficiency, making them ideal for large-scale data with clearly defined relationships. Convex models offer greater flexibility and accommodate complex constraints, ensuring globally optimal solutions in non-linear scenarios where precision and robustness are crucial.
Linear Infographic
 libterm.com
libterm.com