Totally disconnected systems lack any form of connection or interaction between their components, resulting in isolated and independent elements. This property is crucial in topology, where understanding totally disconnected spaces helps analyze the structure and behavior of complex sets. Discover how this concept impacts various fields by reading the rest of the article.
Table of Comparison
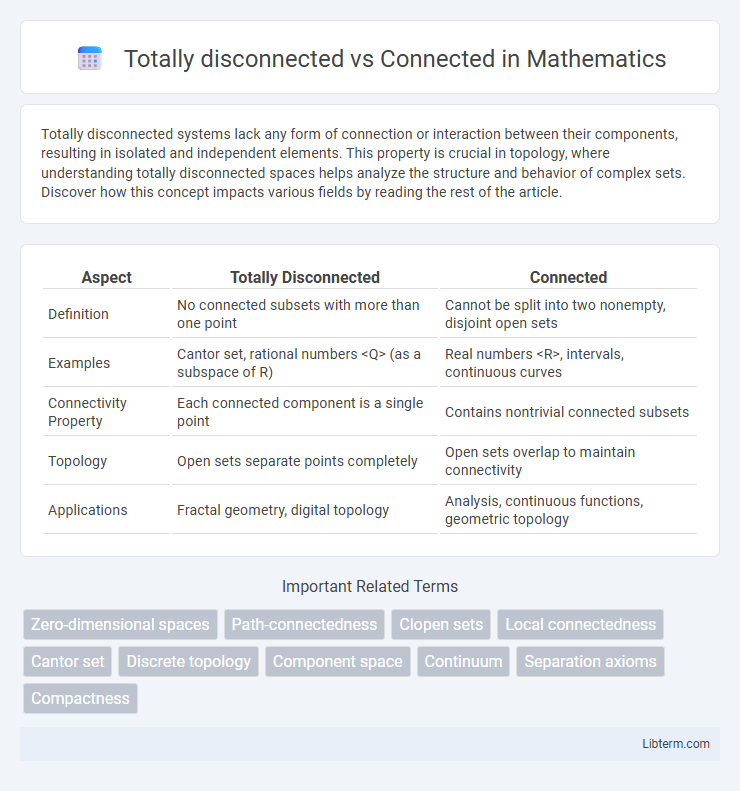
| Aspect | Totally Disconnected | Connected |
|---|---|---|
| Definition | No connected subsets with more than one point | Cannot be split into two nonempty, disjoint open sets |
| Examples | Cantor set, rational numbers <Q> (as a subspace of R) | Real numbers <R>, intervals, continuous curves |
| Connectivity Property | Each connected component is a single point | Contains nontrivial connected subsets |
| Topology | Open sets separate points completely | Open sets overlap to maintain connectivity |
| Applications | Fractal geometry, digital topology | Analysis, continuous functions, geometric topology |
Understanding Connectivity in Mathematical Spaces
Totally disconnected spaces contain no connected subsets larger than single points, illustrating fragmentation at every scale, while connected spaces consist of points joined in a continuous manner without separations. Understanding connectivity in mathematical spaces involves analyzing properties like path-connectedness and component structures, which are fundamental in topology and real analysis. This distinction is crucial for studying phenomena in fractal geometry, measure theory, and dynamical systems where connectivity influences function behavior and space classification.
Defining Totally Disconnected Spaces
Totally disconnected spaces are topological spaces in which the only connected subsets are single points, meaning there are no nontrivial connected components. These spaces lack any continuous path connecting distinct points, highlighting an extreme form of disconnectedness important in areas like fractal geometry and Cantor set analysis. Understanding totally disconnected spaces provides insight into complex structures where connectivity is completely fragmented, contrasting sharply with connected spaces that contain larger continuous subsets.
What Makes a Space Connected?
A space is connected if it cannot be divided into two or more disjoint, nonempty open subsets, meaning any two points within the space can be joined by a continuous path entirely contained in the space. Connectedness implies the absence of separation, ensuring the space is a single piece without isolated components. Totally disconnected spaces lack such paths, consisting exclusively of points or subsets that are isolated from one another topologically.
Key Differences: Connected vs Totally Disconnected
Connected spaces contain no separation into two nonempty disjoint open sets, ensuring continuity and path exist between points, while totally disconnected spaces have no connected subset with more than one point, often consisting of isolated points. Key differences include the presence of continuous paths and connectivity in connected spaces, contrasting with the discrete or fractal structure in totally disconnected spaces. Examples include connected intervals in real numbers versus the Cantor set as a classic totally disconnected space.
Real-Life Examples of Connected Spaces
Connected spaces in topology exemplify seamless continuity, such as the surface of a coffee mug or a donut, where any two points can be joined by a path lying entirely within the object. In everyday scenarios, roads in a city form connected networks allowing uninterrupted travel between locations, contrasting with totally disconnected spaces like isolated islands or separate electronic components where no internal paths connect different parts. Understanding connected spaces enhances navigation, network design, and complex system analysis by emphasizing continuous and unified structures.
Typical Examples of Totally Disconnected Spaces
Typical examples of totally disconnected spaces include the Cantor set, the rational numbers, and the p-adic integers, all characterized by the absence of nontrivial connected subsets. These spaces consist entirely of isolated points or clusters with no continuous paths linking distinct points, exemplifying zero-dimensional topological structures. Understanding these examples is essential in topology, fractal geometry, and number theory for analyzing spaces with disconnected behaviors.
Topological Properties and Implications
Totally disconnected spaces contain no connected subsets other than singletons, indicating every point is isolated within the topology, a property that profoundly affects continuity and limits. Connected spaces cannot be partitioned into two disjoint nonempty open sets, ensuring path-connectedness often facilitates stronger functional and convergence properties. These distinctions influence the behavior of continuous functions, compactness criteria, and separation axioms, critical in fields like functional analysis and dynamical systems.
Continuous Functions and Connectivity
Continuous functions preserve connectivity; the image of a connected space under a continuous function is connected, ensuring no separation occurs. Totally disconnected spaces contain only singletons as connected subsets, making continuous functions from such spaces map into subsets where connectedness is trivial or absent. Understanding the behavior of continuous functions on connected versus totally disconnected spaces clarifies their fundamental topological differences and functional constraints.
Applications in Mathematical Analysis
Totally disconnected spaces, characterized by having no connected subsets other than single points, find crucial applications in areas like fractal geometry, p-adic analysis, and the study of zero-dimensional topological groups, where their structure aids in understanding complex hierarchical patterns and ultrametric spaces. Connected spaces, fundamental in real analysis and topology, enable the use of intermediate value theorems, continuity arguments, and path-connectedness to analyze functions, differential equations, and continuity properties essential for mapping behaviors and convergence criteria. Understanding the distinction between these spaces influences the approach to measure theory, functional analysis, and dynamical systems, as connectedness often shapes the permissible function classes and the nature of solution sets.
Summary: Why Connectivity Matters
Connectivity in topology defines whether a space is in one piece or split into isolated parts, impacting continuity and path traversal. Totally disconnected spaces consist entirely of points without intervals, restricting smooth transitions and complicating function behavior. Connected spaces facilitate seamless interaction and stronger structural properties, crucial for analysis and applications in mathematics and physics.
Totally disconnected Infographic
 libterm.com
libterm.com