Hausdorff measure provides a way to generalize the concept of length, area, and volume to fractal and irregular geometrical sets by using a dimension parameter that can be non-integer. It is crucial for analyzing complex shapes in advanced mathematics, especially in fractal geometry and geometric measure theory. Explore the rest of this article to deepen your understanding of how Hausdorff measure applies to your studies or research.
Table of Comparison
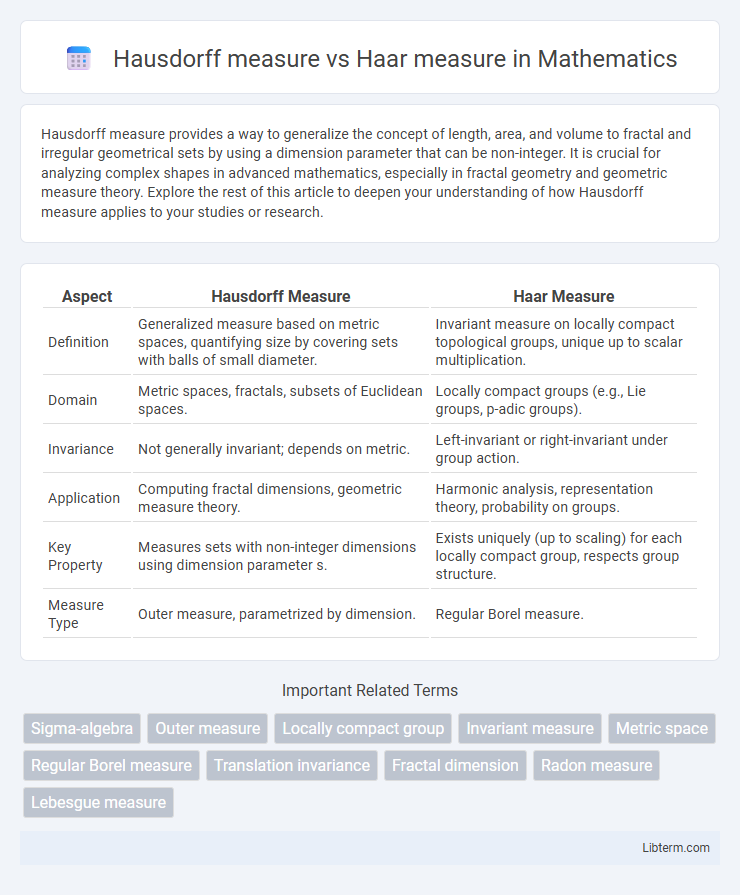
| Aspect | Hausdorff Measure | Haar Measure |
|---|---|---|
| Definition | Generalized measure based on metric spaces, quantifying size by covering sets with balls of small diameter. | Invariant measure on locally compact topological groups, unique up to scalar multiplication. |
| Domain | Metric spaces, fractals, subsets of Euclidean spaces. | Locally compact groups (e.g., Lie groups, p-adic groups). |
| Invariance | Not generally invariant; depends on metric. | Left-invariant or right-invariant under group action. |
| Application | Computing fractal dimensions, geometric measure theory. | Harmonic analysis, representation theory, probability on groups. |
| Key Property | Measures sets with non-integer dimensions using dimension parameter s. | Exists uniquely (up to scaling) for each locally compact group, respects group structure. |
| Measure Type | Outer measure, parametrized by dimension. | Regular Borel measure. |
Introduction to Measure Theory
Hausdorff measure generalizes the concept of length, area, and volume by assigning a measure to fractal sets based on their dimensional properties, crucial in geometric measure theory. Haar measure provides a translation-invariant measure on locally compact topological groups, essential for integrating functions over groups in harmonic analysis. Both measures extend classical measure theory, with Hausdorff focusing on metric spaces and fractal geometry, while Haar emphasizes group structure and invariance.
Defining Hausdorff Measure
Hausdorff measure generalizes the concept of length, area, and volume by assigning a measure to subsets of metric spaces based on their fractal dimension, defined using coverings with sets of diameter at most d and taking limits as d approaches zero. It depends on a scaling parameter called the dimension, allowing the measure to capture intricate geometric properties of irregular sets unlike classical measures. In contrast, Haar measure is a translation-invariant measure defined on locally compact topological groups, primarily used in analysis and representation theory, highlighting their fundamental differences despite both being measures.
Understanding Haar Measure
Haar measure is a fundamental concept in harmonic analysis that provides a way to assign an invariant measure to locally compact topological groups, ensuring translation invariance under group operations. Unlike the Hausdorff measure, which generalizes notions of length, area, and volume to fractal sets by scaling metric spaces, Haar measure applies specifically to group structures, supporting integration on groups like the real numbers, integers, or Lie groups. Understanding Haar measure involves grasping its uniqueness (up to a positive scalar multiple) and its role in defining integrals invariant under the group action, crucial for studying representations and harmonic analysis on groups.
Key Differences Between Hausdorff and Haar Measures
Hausdorff measure generalizes the notion of length, area, and volume to fractal sets by measuring size based on metric space dimensions, whereas Haar measure assigns a translation-invariant measure on locally compact topological groups, crucial for harmonic analysis. Hausdorff measure depends on a chosen dimension parameter and is defined via coverings by sets of small diameter, while Haar measure is unique up to scaling and respects the group structure for integration. Key differences include their application scopes--Hausdorff measure is geometric and fractal dimensional, whereas Haar measure is algebraic and topological, focusing on invariance under group operations.
Applications of Hausdorff Measure
Hausdorff measure plays a crucial role in fractal geometry by quantifying the size of irregular sets that traditional measures cannot capture. It is widely used in geometric measure theory to analyze the dimensional properties of subsets in metric spaces, such as determining the fractal dimension of natural phenomena and mathematical constructs. Applications extend to image processing and dynamical systems, where Hausdorff measure provides insightful metrics for complexity and structure.
Uses of Haar Measure in Mathematics
Haar measure is a fundamental tool in representation theory, harmonic analysis, and ergodic theory, enabling integration on locally compact topological groups with invariance under group translation. It facilitates the study of group actions on spaces and is essential for defining and analyzing probability measures on groups, such as Lie groups and profinite groups. Unlike Hausdorff measure, which quantifies fractal dimensions and geometric sizes in metric spaces, Haar measure provides a canonical way to measure volume in abstract algebraic structures.
Invariance Properties: Hausdorff vs Haar
The Haar measure on a locally compact group is uniquely translation-invariant, meaning it remains unchanged under group elements' left or right multiplication, which is fundamental for harmonic analysis on groups. In contrast, Hausdorff measure is generally defined on metric spaces and is invariant under isometries, preserving distances but not necessarily under group operations unless they coincide with isometries. This distinction makes Haar measure essential for integration on groups, while Hausdorff measure applies broadly in fractal geometry and geometric measure theory.
Examples in Topological Groups
Hausdorff measure generalizes the concept of length, area, and volume to fractal and irregular sets by measuring their size with respect to a metric, often applied in Euclidean spaces or metric groups. Haar measure, uniquely defined up to a scalar multiple on locally compact topological groups, provides an invariant measure under the group operation, crucial for harmonic analysis on groups such as the real numbers under addition or the circle group. For example, on the additive group of real numbers, the Lebesgue measure is both the Haar measure and coincides with the 1-dimensional Hausdorff measure, illustrating the overlap and difference in their construction and applications in topological groups.
Measure Uniqueness and Normalization
Hausdorff measure is uniquely defined on metric spaces through scaling limits of coverings with sets of small diameter, normalized by a dimension parameter to capture fractal geometry, whereas Haar measure is the unique translation-invariant measure on locally compact topological groups, normalized so that a chosen compact set has measure one. The uniqueness of Haar measure is guaranteed up to a positive scalar multiple relying on the group structure, while Hausdorff measure uniqueness depends on the dimension used for the metric space. Normalization in Haar measure often fixes total measure on compact groups, contrasting with Hausdorff measure normalization that sets scale constants tied to geometric dimension.
Conclusion: Choosing the Appropriate Measure
Choosing the appropriate measure depends on the underlying structure and application context: Hausdorff measure excels in analyzing fractal geometry and irregular sets by capturing their dimensional properties, while Haar measure is essential for integrating functions over locally compact topological groups due to its translation invariance. Hausdorff measure generalizes Lebesgue measure to non-integer dimensions, making it ideal for geometric measure theory, whereas Haar measure provides a vital tool in harmonic analysis and representation theory through its unique invariant measure on groups. Understanding the mathematical framework and goals ensures the selection of the correct measure for precise and meaningful results.
Hausdorff measure Infographic
 libterm.com
libterm.com