A Lebesgue measurable set is a fundamental concept in measure theory, defined so that its size or volume can be consistently assigned in terms of Lebesgue measure. These sets are critical for integrating functions and understanding advanced probability and analysis. Explore the article to learn how Lebesgue measurable sets shape modern mathematical analysis.
Table of Comparison
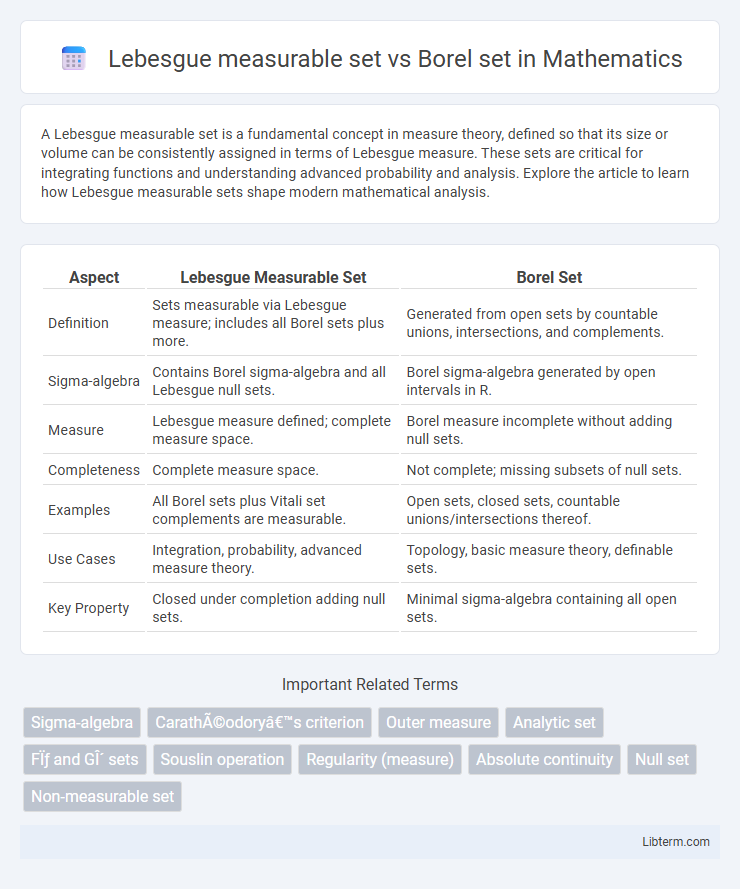
| Aspect | Lebesgue Measurable Set | Borel Set |
|---|---|---|
| Definition | Sets measurable via Lebesgue measure; includes all Borel sets plus more. | Generated from open sets by countable unions, intersections, and complements. |
| Sigma-algebra | Contains Borel sigma-algebra and all Lebesgue null sets. | Borel sigma-algebra generated by open intervals in R. |
| Measure | Lebesgue measure defined; complete measure space. | Borel measure incomplete without adding null sets. |
| Completeness | Complete measure space. | Not complete; missing subsets of null sets. |
| Examples | All Borel sets plus Vitali set complements are measurable. | Open sets, closed sets, countable unions/intersections thereof. |
| Use Cases | Integration, probability, advanced measure theory. | Topology, basic measure theory, definable sets. |
| Key Property | Closed under completion adding null sets. | Minimal sigma-algebra containing all open sets. |
Introduction to Measurable Sets
A Borel set is any set that can be formed from open or closed sets through countable unions, intersections, and complements, forming the Borel sigma-algebra. Lebesgue measurable sets extend this concept by including sets that differ from Borel sets by a null set, enabling measurement of more complex subsets in real analysis. The Lebesgue sigma-algebra contains all Borel sets as well as additional sets necessary for a complete measure, which is crucial for integration and probability theory.
Defining Lebesgue Measurable Sets
Lebesgue measurable sets are defined as subsets of the real numbers for which the measure can be consistently extended from Borel sets to include more complex sets through completion with respect to the Lebesgue measure. Every Borel set is Lebesgue measurable, but Lebesgue measurable sets also include sets obtained by adding or subtracting null sets from Borel sets, allowing a richer sigma-algebra. This extension ensures that all subsets differing from a Borel set by a measure-zero set are captured within the Lebesgue measurable framework.
Understanding Borel Sets
Borel sets, generated from open sets through countable unions, intersections, and complements, form the smallest s-algebra containing all open subsets of a topological space, making them fundamental in measure theory. Lebesgue measurable sets extend beyond Borel sets by including sets differing from Borel sets by a null set, thus allowing the inclusion of more complex subsets for defining the Lebesgue measure. Understanding Borel sets is crucial as they provide the groundwork for defining measurable functions, integration, and probability on well-structured spaces.
Generating Borel Sets: Sigma-Algebra Construction
Generating Borel sets involves constructing the smallest sigma-algebra containing all open sets in a given topological space, ensuring closure under countable unions, countable intersections, and complements. Lebesgue measurable sets extend Borel sets by including sets that differ from Borel sets by a null set, achieved through completion of the Borel sigma-algebra with respect to the Lebesgue measure. This completion process incorporates more subsets, enabling the measurement of a wider class of sets beyond the original Borel sigma-algebra.
Relationship Between Lebesgue and Borel Sets
Lebesgue measurable sets include all Borel sets along with sets obtained by adding or removing subsets of Borel null sets, making the collection of Lebesgue measurable sets strictly larger than the Borel sigma-algebra. Every Borel set is Lebesgue measurable, but not all Lebesgue measurable sets are Borel, as Lebesgue measurability allows for completion under Lebesgue measure. This relationship highlights the extension from Borel sigma-algebra to the Lebesgue sigma-algebra through the process of measure completion.
Key Examples: Sets That Are Lebesgue Measurable but Not Borel
Sets that are Lebesgue measurable but not Borel include Vitali sets constructed using equivalence classes modulo rational numbers, which demonstrate non-Borel measurability. Another key example involves subsets derived from well-orderings of the real numbers, where the complexity surpasses Borel hierarchy but remains Lebesgue measurable due to null differences. These examples highlight the distinction between the broader Lebesgue s-algebra, which includes more complex sets than the Borel s-algebra generated by open intervals.
Properties and Structure of Borel Sets
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the smallest s-algebra containing all open subsets in a topological space. Their hierarchical structure is described by the Borel hierarchy, which classifies sets into levels based on complexity, such as \( \Sigma^0_n \) and \( \Pi^0_n \) classes. Borel sets are well-behaved with respect to continuous mappings, preserving measurability, and are a subset of Lebesgue measurable sets, which include additional sets constructed via completion with respect to a measure.
Significance of Lebesgue Measurability in Analysis
Lebesgue measurable sets extend the concept of measurability beyond Borel sets by including all subsets of real numbers that can be approximated using Borel sets with negligible difference in measure. This broader class is crucial in analysis as it supports the full development of Lebesgue integration, allowing integrals of more complex functions and facilitating convergence theorems like the Dominated Convergence Theorem. The significance lies in enabling rigorous treatment of limits and functions that are not Borel measurable, thereby enhancing the flexibility and power of modern measure theory in mathematical analysis.
Applications in Probability and Real Analysis
Lebesgue measurable sets form the foundation for defining integrals that handle a broader class of functions than Borel sets, enabling accurate probability measures on complex events in probability theory. Borel sets, generated from open intervals through countable operations, serve as the basis for standard probability spaces but lack closure under limit operations critical for advanced real analysis. The extension from Borel to Lebesgue measurable sets allows for the rigorous treatment of integration, convergence theorems, and construction of probability measures on more intricate sigma-algebras encountered in stochastic processes and functional analysis.
Summary and Key Differences
Lebesgue measurable sets include all Borel sets along with subsets of null sets, allowing for a more extensive collection defined via completion of the Borel sigma-algebra with respect to Lebesgue measure. Borel sets arise from the sigma-algebra generated by open sets in a topological space, making them fundamental in descriptive set theory but sometimes insufficient for measure-theoretic purposes. Key differences lie in their construction--Borel sets rely on topological operations, whereas Lebesgue measurable sets incorporate measure completion, enhancing practical applications in integration and probability theory.
Lebesgue measurable set Infographic
 libterm.com
libterm.com