Quaternions are a number system extending complex numbers, crucial for representing rotations in three-dimensional space without singularities or gimbal lock. Widely used in computer graphics, robotics, and aerospace, they provide smooth interpolation and efficient computation for orientation and rotation tasks. Discover how quaternions can enhance Your understanding of 3D transformations by reading the rest of this article.
Table of Comparison
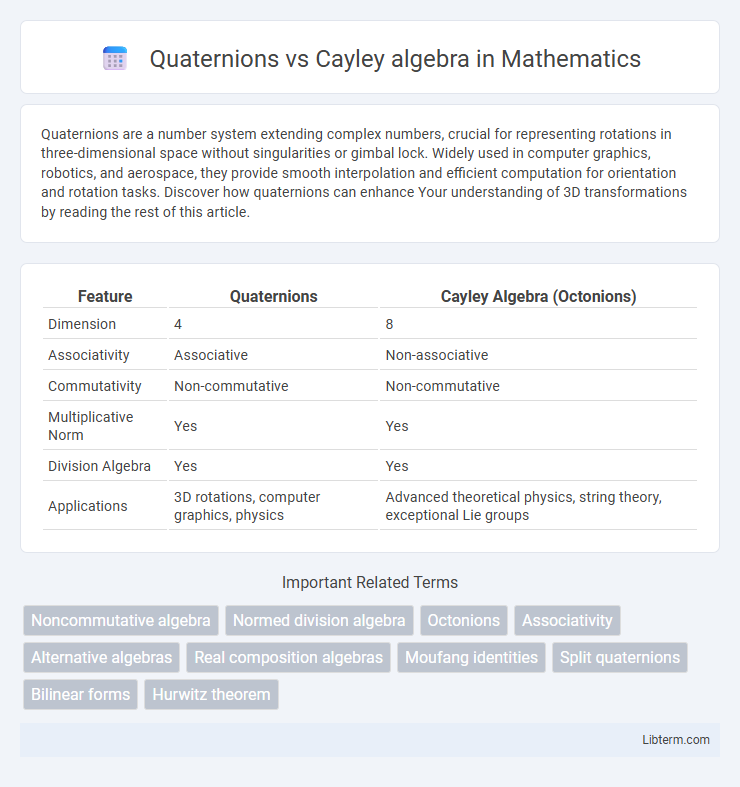
| Feature | Quaternions | Cayley Algebra (Octonions) |
|---|---|---|
| Dimension | 4 | 8 |
| Associativity | Associative | Non-associative |
| Commutativity | Non-commutative | Non-commutative |
| Multiplicative Norm | Yes | Yes |
| Division Algebra | Yes | Yes |
| Applications | 3D rotations, computer graphics, physics | Advanced theoretical physics, string theory, exceptional Lie groups |
Introduction to Quaternions and Cayley Algebra
Quaternions are a four-dimensional normed division algebra over the real numbers, introduced by William Rowan Hamilton in 1843, and widely used to represent rotations in three-dimensional space. Cayley algebra, also known as octonions, extends quaternions to an eight-dimensional non-associative algebra, discovered by Arthur Cayley, with applications in theoretical physics and higher-dimensional geometry. Both structures provide foundational frameworks in algebra and geometry, with quaternions maintaining associativity while Cayley algebra relaxes this property, leading to richer algebraic behaviors.
Historical Background and Development
Quaternions, introduced by William Rowan Hamilton in 1843, marked a pioneering expansion of complex numbers into four-dimensional space, providing an algebraic framework for rotations in three dimensions. Cayley algebra, or octonions, discovered by Arthur Cayley in 1845, extended quaternions into an eight-dimensional non-associative algebra, contributing significantly to the study of normed division algebras. Both structures emerged from 19th-century efforts to generalize complex numbers and laid foundational principles in modern algebra and geometry.
Mathematical Foundations: Definitions and Structures
Quaternions are a four-dimensional normed division algebra over the real numbers, defined by the basis elements {1, i, j, k} and the multiplication rules i2 = j2 = k2 = ijk = -1, exhibiting non-commutative but associative properties. Cayley algebra, also known as octonions, extends quaternions to an eight-dimensional algebra with basis elements {1, e1, e2, e3, e4, e5, e6, e7}, characterized by non-associative but alternative multiplication and a norm preserving property. Both algebras are examples of normed division algebras, with quaternions forming an associative structure and the Cayley algebra representing the largest normed division algebra accommodating non-associativity through the use of the Moufang identities.
Dimensionality: 4D Quaternions vs 8D Cayley Algebra
Quaternions are a 4-dimensional normed division algebra over the real numbers, extensively used for representing rotations in 3D space due to their compact and non-commutative properties. Cayley algebra, also known as octonions, extends this structure to an 8-dimensional normed division algebra, introducing non-associativity while maintaining norm multiplicativity. The dimensionality difference between 4D quaternions and 8D octonions reflects a progression in algebraic complexity, impacting their respective applications in geometry, physics, and computer graphics.
Algebraic Properties and Differences
Quaternions form a four-dimensional non-commutative associative algebra over the real numbers, defined by the basis elements 1, i, j, and k, with multiplication rules that satisfy i2 = j2 = k2 = ijk = -1. Cayley algebra, also known as octonions, extends quaternions to an eight-dimensional normed division algebra that is non-associative but alternative, characterized by the loss of associativity while retaining a weaker form of algebraic structure. The primary algebraic difference is that quaternions maintain associativity, enabling straightforward algebraic manipulations, whereas Cayley algebra's non-associativity complicates computations but allows richer structure related to exceptional Lie groups.
Noncommutativity and Nonassociativity Compared
Quaternions exhibit noncommutativity, meaning the order of multiplication affects the result, but they retain associativity, ensuring consistent grouping in multiplication operations. In contrast, Cayley algebra, or octonions, displays both noncommutativity and nonassociativity, with multiplication not only dependent on order but also on how elements are grouped. This distinction impacts their applications, where quaternions are preferred in 3D rotations for their associative property, while octonions offer richer, though more complex, algebraic structures used in advanced theoretical physics.
Applications in Physics and Engineering
Quaternions, extensively used in robotics and aerospace engineering, provide efficient, singularity-free representations of 3D rotations, essential for attitude control and computer graphics. Cayley algebra, including octonions, finds emerging applications in theoretical physics, particularly in string theory and particle physics, offering frameworks for describing symmetries and higher-dimensional spaces. The practical use of quaternions in real-time rotational dynamics contrasts with Cayley algebra's role in advanced mathematical models for unified physical theories.
Visualization and Geometric Interpretations
Quaternions provide a clear geometric interpretation as rotations in three-dimensional space, enabling intuitive visualization through axis-angle representations and unit sphere mappings. Cayley algebra, or octonions, extend this framework into eight dimensions but complicate visualization due to non-associativity and higher dimensionality, making geometric interpretations less straightforward. While quaternions correspond directly to rotations preserving orientation and norm, Cayley algebra's structure challenges conventional spatial visualization, requiring more abstract mathematical tools for geometric insights.
Computational Challenges and Efficiencies
Quaternions provide a computationally efficient framework for representing rotations with fewer arithmetic operations and less computational overhead compared to Cayley algebras, which involve more complex, higher-dimensional calculations. The non-associative nature of Cayley (octonion) algebra introduces significant challenges in algorithm implementation, leading to increased computational complexity and difficulties in maintaining numerical stability. Quaternions excel in applications requiring real-time performance and stability, such as computer graphics and robotics, while Cayley algebras, despite their mathematical richness, remain less practical for computationally intensive tasks.
Conclusion: Choosing Between Quaternions and Cayley Algebra
Quaternions offer a robust and computationally efficient framework for 3D rotations and are widely used in computer graphics, robotics, and aerospace engineering. Cayley algebra, or octonions, provide a richer yet more complex structure applicable in advanced theoretical physics and higher-dimensional mathematics, though they lack associativity, complicating their practical use. The choice between quaternions and Cayley algebra depends on the application's requirements for algebraic properties, dimensional complexity, and computational efficiency.
Quaternions Infographic
 libterm.com
libterm.com