Riemannian manifolds provide a rigorous framework for analyzing curved spaces through the use of smoothly varying inner products on tangent spaces. These structures enable the extension of geometric concepts such as distances, angles, and curvature to more general, non-Euclidean settings. Discover how understanding Riemannian manifolds can deepen your grasp of geometry and its applications throughout this article.
Table of Comparison
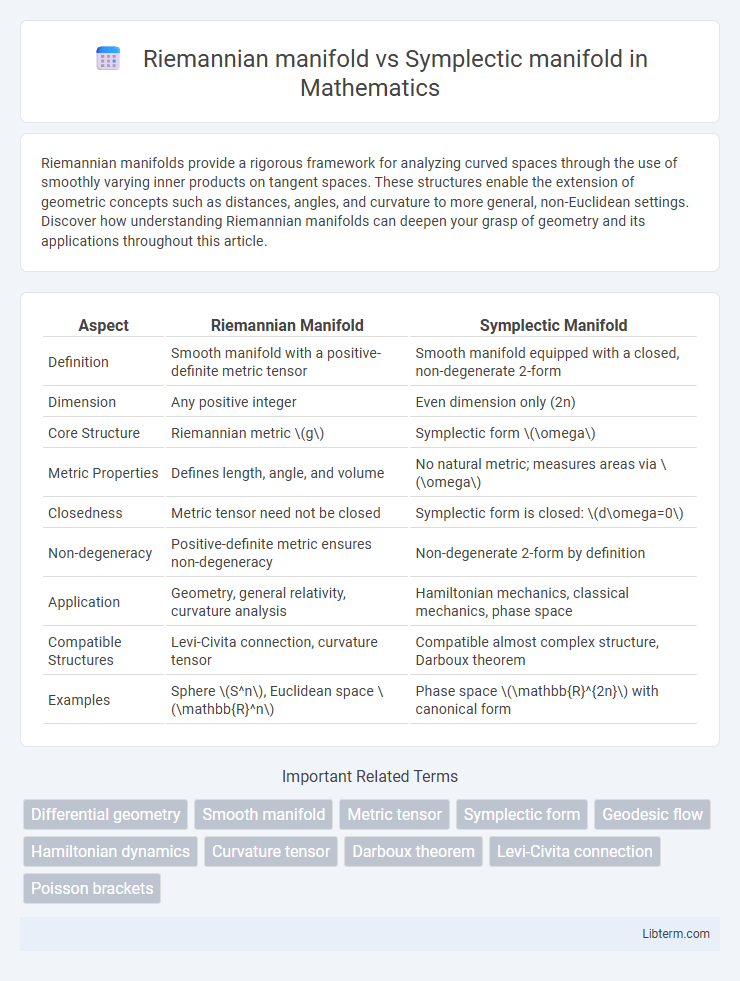
| Aspect | Riemannian Manifold | Symplectic Manifold |
|---|---|---|
| Definition | Smooth manifold with a positive-definite metric tensor | Smooth manifold equipped with a closed, non-degenerate 2-form |
| Dimension | Any positive integer | Even dimension only (2n) |
| Core Structure | Riemannian metric \(g\) | Symplectic form \(\omega\) |
| Metric Properties | Defines length, angle, and volume | No natural metric; measures areas via \(\omega\) |
| Closedness | Metric tensor need not be closed | Symplectic form is closed: \(d\omega=0\) |
| Non-degeneracy | Positive-definite metric ensures non-degeneracy | Non-degenerate 2-form by definition |
| Application | Geometry, general relativity, curvature analysis | Hamiltonian mechanics, classical mechanics, phase space |
| Compatible Structures | Levi-Civita connection, curvature tensor | Compatible almost complex structure, Darboux theorem |
| Examples | Sphere \(S^n\), Euclidean space \(\mathbb{R}^n\) | Phase space \(\mathbb{R}^{2n}\) with canonical form |
Introduction to Manifolds
Riemannian manifolds are smooth manifolds equipped with a Riemannian metric, allowing the measurement of angles, distances, and volumes, making them fundamental in differential geometry and general relativity. Symplectic manifolds possess a closed, non-degenerate 2-form called a symplectic form, essential in Hamiltonian mechanics and the study of phase spaces. Both structures enhance the understanding of manifolds by providing distinct geometric frameworks for analyzing curvature and dynamical systems respectively.
Defining Riemannian Manifolds
Riemannian manifolds are smooth manifolds equipped with a Riemannian metric, a positive-definite inner product on the tangent space that varies smoothly from point to point, enabling the measurement of lengths and angles. This metric induces notions of distance, angle, volume, and curvature, which are fundamental in differential geometry and general relativity. Unlike symplectic manifolds, which possess a closed, non-degenerate 2-form used to model phase spaces in classical mechanics, Riemannian manifolds focus on geometric structures compatible with smooth, metric-based analysis.
Key Features of Riemannian Geometry
Riemannian geometry centers on smooth manifolds equipped with a Riemannian metric, enabling the measurement of angles, distances, and curvature. Key features include a positive-definite metric tensor, geodesics as shortest paths, and the Levi-Civita connection ensuring metric compatibility and torsion-free properties. Unlike symplectic manifolds focused on even-dimensional structures with non-degenerate, closed 2-forms, Riemannian manifolds emphasize metric structure for geometric analysis and curvature-based phenomena.
Understanding Symplectic Manifolds
Symplectic manifolds are smooth even-dimensional spaces equipped with a closed, non-degenerate 2-form called the symplectic form, which provides a geometric framework for classical mechanics and Hamiltonian systems. Unlike Riemannian manifolds that rely on a positive-definite metric tensor to measure distances and angles, symplectic manifolds emphasize area-preserving transformations and the study of phase space dynamics. Understanding symplectic geometry involves analyzing structures that preserve the symplectic form, enabling the exploration of conserved quantities and integrable systems.
Distinct Characteristics of Symplectic Geometry
Symplectic manifolds are characterized by a closed, non-degenerate 2-form called the symplectic form, which lacks a metric structure present in Riemannian manifolds. Unlike Riemannian geometry, symplectic geometry focuses on preserving volume under Hamiltonian flows rather than distance or angles. This distinct structure enables the study of phase space in classical mechanics, emphasizing properties like canonical transformations and Poisson brackets.
Structural Differences: Metric vs. Symplectic Forms
Riemannian manifolds are characterized by a positive-definite metric tensor that defines distances and angles, enabling measurement of length and curvature. Symplectic manifolds possess a closed, non-degenerate 2-form called the symplectic form, which provides a framework for volume preservation and Hamiltonian dynamics but lacks a notion of distance. The fundamental structural difference lies in Riemannian manifolds' metric tensor used for geometric measurements versus symplectic manifolds' antisymmetric symplectic form governing phase space geometry.
Examples of Riemannian and Symplectic Manifolds
The 2-sphere \( S^2 \) with the standard round metric exemplifies a Riemannian manifold, providing a smooth structure equipped with a positive-definite metric tensor measuring lengths and angles. In contrast, the cotangent bundle \( T^*M \) of a smooth manifold \( M \) serves as a canonical example of a symplectic manifold, carrying a non-degenerate, closed 2-form called the symplectic form essential for Hamiltonian mechanics. Complex projective spaces \( \mathbb{CP}^n \) also illustrate manifolds that admit both Riemannian and symplectic structures, bridging these two geometric frameworks.
Applications in Mathematics and Physics
Riemannian manifolds provide the mathematical foundation for understanding curved spaces in general relativity, enabling the precise description of gravitational phenomena through metrics and geodesics. Symplectic manifolds underpin Hamiltonian mechanics, facilitating the study of phase space dynamics and conservation laws in classical and quantum physics. Both structures are essential in differential geometry and mathematical physics, with Riemannian geometry focusing on distance and angles, while symplectic geometry emphasizes the structure of energy-preserving transformations.
Interrelations and Overlaps Between Both Structures
Riemannian and symplectic manifolds both provide rich geometric frameworks with distinct structures: Riemannian manifolds are equipped with a metric tensor enabling measurement of angles and distances, while symplectic manifolds possess a closed, nondegenerate 2-form fundamental to classical mechanics. Overlaps occur in almost Kahler manifolds, where a Riemannian metric, a symplectic form, and an almost complex structure coexist compatibly, blending properties of both geometries. This interrelation enables the use of techniques from Riemannian geometry in the study of symplectic topology and vice versa, enriching fields like geometric quantization and complex geometry.
Summary: Choosing Between Riemannian and Symplectic Manifolds
Riemannian manifolds provide a structure equipped with a smoothly varying positive-definite metric tensor, enabling the measurement of lengths and angles, ideal for modeling geometric properties in general relativity and differential geometry. Symplectic manifolds, characterized by a non-degenerate, closed 2-form, serve as the mathematical foundation for Hamiltonian mechanics and phase space analysis in classical and quantum physics. Selecting between Riemannian and Symplectic manifolds depends on whether the focus is on metric properties and curvature or on conserved quantities and dynamical systems in physics.
Riemannian manifold Infographic
 libterm.com
libterm.com