Diffeomorphic transformations preserve the smooth structure between shapes, ensuring continuous and invertible mappings without tearing or folding. This concept is crucial in fields like computer vision, medical imaging, and geometric modeling for accurate shape analysis and registration. Explore the article to understand how diffeomorphic methods can enhance your applications.
Table of Comparison
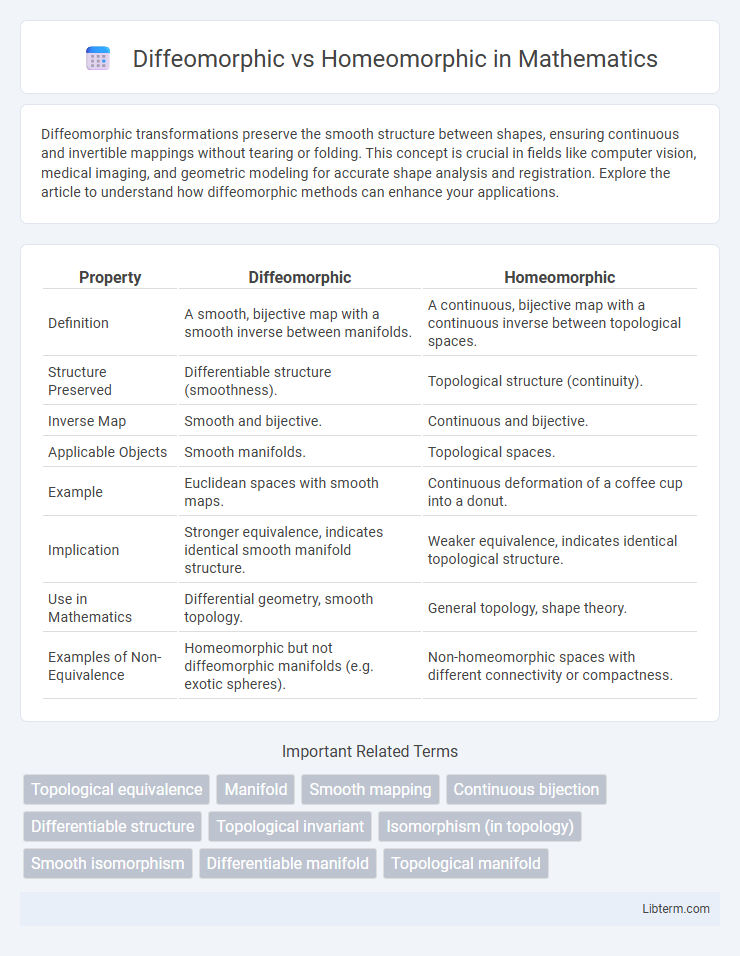
| Property | Diffeomorphic | Homeomorphic |
|---|---|---|
| Definition | A smooth, bijective map with a smooth inverse between manifolds. | A continuous, bijective map with a continuous inverse between topological spaces. |
| Structure Preserved | Differentiable structure (smoothness). | Topological structure (continuity). |
| Inverse Map | Smooth and bijective. | Continuous and bijective. |
| Applicable Objects | Smooth manifolds. | Topological spaces. |
| Example | Euclidean spaces with smooth maps. | Continuous deformation of a coffee cup into a donut. |
| Implication | Stronger equivalence, indicates identical smooth manifold structure. | Weaker equivalence, indicates identical topological structure. |
| Use in Mathematics | Differential geometry, smooth topology. | General topology, shape theory. |
| Examples of Non-Equivalence | Homeomorphic but not diffeomorphic manifolds (e.g. exotic spheres). | Non-homeomorphic spaces with different connectivity or compactness. |
Understanding Diffeomorphic and Homeomorphic Concepts
Diffeomorphic and homeomorphic concepts describe different types of equivalences between topological spaces; homeomorphic maps are continuous functions with continuous inverses preserving topological properties, while diffeomorphic maps are smooth bijections with smooth inverses preserving differentiable structures. Understanding diffeomorphism requires familiarity with smooth manifolds and differential calculus, while homeomorphism focuses on general topological equivalences without smoothness constraints. The distinction is crucial in fields like differential geometry and topology, where the nature of equivalence influences the types of properties and invariants studied.
Mathematical Definitions: Diffeomorphism vs Homeomorphism
Diffeomorphism is a smooth, invertible map between differentiable manifolds with a smooth inverse, preserving the structures required for calculus. Homeomorphism is a continuous, bijective map between topological spaces with a continuous inverse, preserving topological properties but not necessarily differentiability. The main distinction lies in the requirement of differentiability in diffeomorphisms, making them stronger than homeomorphisms in the context of smooth manifolds.
Topological Properties and Invariants
Diffeomorphic and homeomorphic maps both preserve topological properties, but diffeomorphisms require smoothness, ensuring differentiable structures align exactly between manifolds. Homeomorphisms maintain topological invariants such as connectedness, compactness, and genus without necessarily preserving geometric or smooth structures. Topological invariants under homeomorphisms include fundamental groups and homology, while diffeomorphisms also preserve differentiable invariants like tangent bundle isomorphisms and smooth vector fields.
Smoothness vs Continuity: Key Differences
Diffeomorphic maps are smooth bijections with smooth inverses, ensuring differentiability and preserving geometric structures, while homeomorphic maps guarantee only continuous bijections with continuous inverses, focusing on topological equivalence without requiring smoothness. The key difference lies in smoothness: diffeomorphisms maintain differentiable structures enabling calculus on manifolds, whereas homeomorphisms allow deformations like stretching or bending but prohibit tearing or gluing, preserving continuity alone. This distinction is crucial in topology and differential geometry, where smoothness affects manifold classification and functional analysis.
Real-World Examples of Each Mapping
Diffeomorphic mappings, such as those used in medical imaging for accurate brain deformation modeling, preserve smooth structures and enable precise analysis of complex shapes. Homeomorphic mappings, exemplified by stretching a coffee cup into a donut shape without tearing, illustrate continuous transformations preserving topological properties but allowing for non-smooth changes. In engineering, diffeomorphisms are critical for fluid dynamics simulations requiring differentiability, while topology-driven material science applications often rely on homeomorphisms to study structural continuity under deformation.
Importance in Differential Topology and Geometry
Diffeomorphic and homeomorphic concepts are fundamental in differential topology and geometry, as they distinguish between smooth and continuous deformations of manifolds. A diffeomorphism implies a smooth, invertible mapping preserving differentiable structures, crucial for analyzing geometric properties and curvature. Homeomorphisms maintain topological equivalence without smoothness, serving to identify topological invariants but lacking the finer detail needed for differential analysis.
Criteria for Diffeomorphic and Homeomorphic Relations
Diffeomorphic relations require a bijective, differentiable map with a differentiable inverse between manifolds, ensuring smooth structure compatibility and preserving differential properties. Homeomorphic relations demand a continuous, bijective map with a continuous inverse, focusing solely on topological equivalence without smoothness constraints. Criteria for diffeomorphism emphasize differentiability class \( C^r \) and smooth manifold structure, while criteria for homeomorphism center on topological continuity and bijection.
Applications in Mathematics and Physics
Diffeomorphic transformations preserve smooth structure and differentiability, making them crucial in fields like differential geometry, dynamical systems, and general relativity for modeling smooth manifolds and spacetime deformations. Homeomorphic mappings emphasize continuous deformation without tearing, playing a key role in topology, knot theory, and complex analysis by classifying spaces based on their intrinsic connectivity properties. In physics, diffeomorphisms underpin the formulation of Einstein's field equations, while homeomorphisms assist in studying topological phases and quantum field theory through continuous topological equivalence.
Common Misconceptions and Clarifications
Diffeomorphic and homeomorphic concepts both describe equivalences between spaces, but diffeomorphisms require smoothness and differentiability, whereas homeomorphisms only require continuous mappings with continuous inverses. A common misconception is that all homeomorphic spaces are also diffeomorphic, which is false since differentiable structures may vary even if the underlying topological spaces are equivalent. Clarifying this distinction is crucial in differential topology, as it impacts the classification of manifolds and the study of smooth structures.
Summary: Choosing Between Diffeomorphism and Homeomorphism
Diffeomorphism involves a smooth, invertible mapping with continuous derivatives between manifolds, ensuring differentiable structures are preserved, while homeomorphism requires only a continuous, bijective mapping with a continuous inverse, preserving topological properties without guaranteeing differentiability. Choosing between diffeomorphism and homeomorphism depends on whether the focus is on preserving geometric and smooth structures (diffeomorphism) or just the topological equivalence and continuity of spaces (homeomorphism). In fields like differential geometry and smooth manifold theory, diffeomorphisms are essential for analyzing smooth structures, whereas topology prioritizes homeomorphisms for studying shape and connectivity regardless of smoothness.
Diffeomorphic Infographic
 libterm.com
libterm.com