Markov models are powerful tools for predicting sequences by using probabilities based on previous states. These models have widespread applications in fields such as natural language processing, finance, and genetics. Discover how Markov models can enhance your data analysis and decision-making by exploring the full article.
Table of Comparison
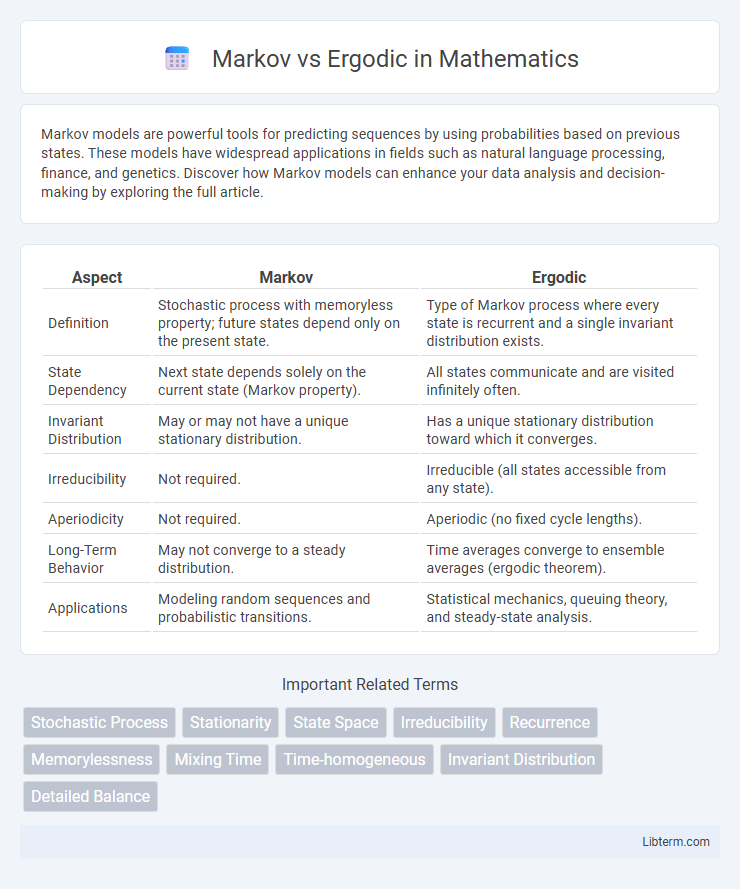
| Aspect | Markov | Ergodic |
|---|---|---|
| Definition | Stochastic process with memoryless property; future states depend only on the present state. | Type of Markov process where every state is recurrent and a single invariant distribution exists. |
| State Dependency | Next state depends solely on the current state (Markov property). | All states communicate and are visited infinitely often. |
| Invariant Distribution | May or may not have a unique stationary distribution. | Has a unique stationary distribution toward which it converges. |
| Irreducibility | Not required. | Irreducible (all states accessible from any state). |
| Aperiodicity | Not required. | Aperiodic (no fixed cycle lengths). |
| Long-Term Behavior | May not converge to a steady distribution. | Time averages converge to ensemble averages (ergodic theorem). |
| Applications | Modeling random sequences and probabilistic transitions. | Statistical mechanics, queuing theory, and steady-state analysis. |
Introduction to Markov and Ergodic Concepts
Markov processes describe systems where the next state depends solely on the current state, not on the sequence of events that preceded it, emphasizing memoryless transitions. Ergodic theory studies the long-term average behavior of dynamical systems, ensuring that time averages and ensemble averages converge under certain conditions. Understanding Markov and ergodic concepts enables analysis of stochastic stability and predictability in complex systems.
Defining Markov Processes
Markov processes are stochastic models characterized by the memoryless property, where the future state depends solely on the current state, not on the sequence of events that preceded it. Ergodic processes are a subset of Markov processes where every state is recurrent and positive recurrent, ensuring long-term statistical properties are stable and time averages converge to ensemble averages. Defining Markov processes involves specifying the state space, transition probabilities or transition rates, and the Markov property, which governs the process's evolution over time without dependence on past trajectories.
Understanding Ergodicity
Ergodicity in stochastic processes refers to the property where time averages and ensemble averages are equivalent, enabling long-term predictions from single sample paths. Unlike general Markov processes, which emphasize memoryless transitions between states, ergodic processes guarantee convergence to a unique stationary distribution regardless of the initial state. Understanding ergodicity is essential in fields such as statistical physics, finance, and signal processing, where consistent long-term behavior is critical.
Key Differences Between Markov and Ergodic Systems
Markov systems are defined by the memoryless property, where the next state depends solely on the current state, while ergodic systems ensure that long-term state probabilities are independent of initial conditions. Ergodicity implies that a Markov chain is irreducible and aperiodic, allowing every state to be recurrent and visited infinitely often. The key difference lies in ergodic systems guaranteeing statistical regularity and convergence over time, whereas Markov systems may not necessarily exhibit such uniform long-term behavior.
Mathematical Foundations of Markov Models
Markov models rely on the mathematical foundation of Markov chains, characterized by memoryless property where the future state depends solely on the current state, not on the sequence of events that preceded it. Ergodicity in Markov chains ensures that long-term state probabilities exist and are independent of the initial state, providing a stable distribution crucial for applications in stochastic processes. The distinction lies in ergodic chains being irreducible and aperiodic, guaranteeing convergence to a unique stationary distribution, which is fundamental for reliable predictions in Markov-based models.
Properties and Criteria for Ergodicity
Markov chains are stochastic processes with memoryless transitions between states, whereas ergodic Markov chains possess properties ensuring long-term statistical behavior is independent of initial states. Ergodicity requires the chain to be both irreducible, meaning every state can be reached from any other state, and aperiodic, indicating the system does not cycle in fixed intervals. These criteria guarantee convergence to a unique stationary distribution, enabling reliable long-term predictions.
Real-world Applications: Markov vs. Ergodic
Markov processes model systems where the future state depends only on the current state, making them ideal for applications in finance, weather forecasting, and speech recognition. Ergodic processes ensure long-term average behavior is independent of initial conditions, crucial for statistical physics, network traffic analysis, and queuing theory. Real-world systems leverage Markov properties for short-term prediction and ergodicity for understanding steady-state behaviors over time.
Advantages and Limitations of Markov Chains
Markov chains provide a powerful framework for modeling stochastic processes where future states depend only on the current state, enabling efficient computation of state probabilities and prediction in complex systems. The advantage of Markov chains lies in their simplicity and memoryless property, which allows for tractable analysis and applications in fields such as finance, genetics, and queueing theory. However, limitations include the assumption of state independence from past history and potential challenges in modeling systems with long-term dependencies or non-stationary transition probabilities.
Practical Implications of Ergodic Systems
Ergodic systems ensure that time averages converge to ensemble averages, making long-term predictions possible from single sample paths in practical applications such as statistical mechanics and financial modeling. In contrast, Markov systems describe memoryless processes with state transitions dependent only on the current state, but not all Markov chains are ergodic, which limits their predictive reliability without ergodicity. Ergodicity guarantees system stability and representative sampling, essential for designing algorithms in machine learning and optimizing stochastic simulations.
Conclusion: Choosing Between Markov and Ergodic Approaches
Choosing between Markov and Ergodic models depends on the nature of the system and the desired analysis outcomes. Markov models excel in scenarios with memoryless stochastic processes where state transitions depend solely on the current state, providing precise short-term predictions. Ergodic models are preferred for long-term statistical properties, ensuring that time averages converge to ensemble averages for systems with stable, recurring behaviors.
Markov Infographic
 libterm.com
libterm.com