The Hilbert series is a powerful tool in algebraic geometry and commutative algebra that encodes the dimension of graded components of a graded ring or module. It reveals important information about the growth of dimensions in each graded degree, serving as a generating function that connects algebraic and combinatorial properties. Discover how the Hilbert series can deepen your understanding of algebraic structures by exploring the rest of this article.
Table of Comparison
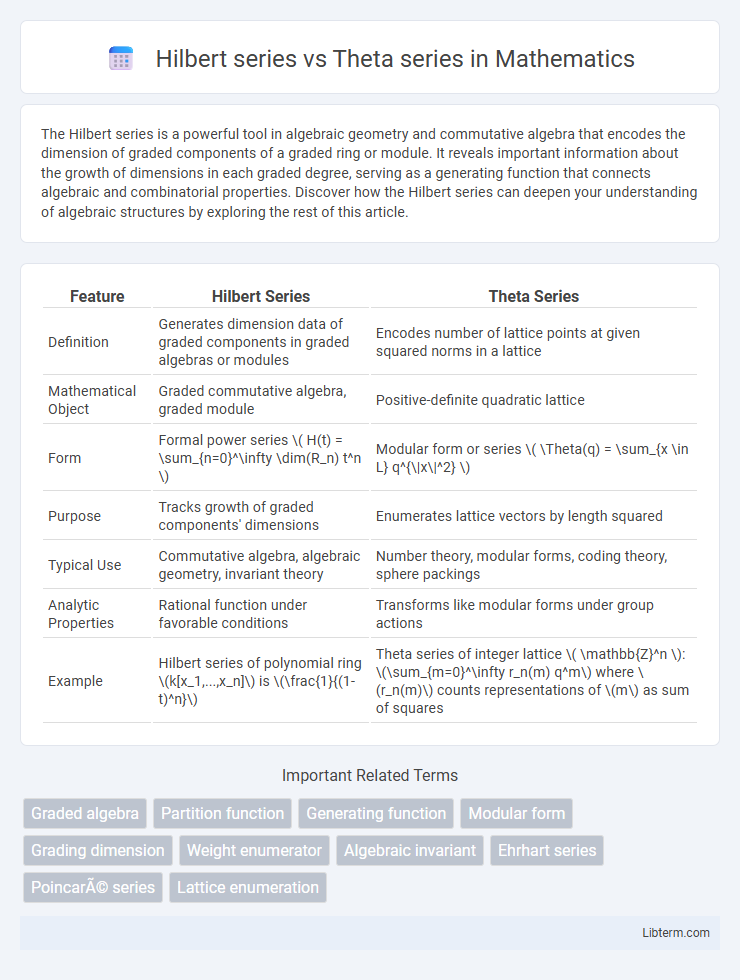
| Feature | Hilbert Series | Theta Series |
|---|---|---|
| Definition | Generates dimension data of graded components in graded algebras or modules | Encodes number of lattice points at given squared norms in a lattice |
| Mathematical Object | Graded commutative algebra, graded module | Positive-definite quadratic lattice |
| Form | Formal power series \( H(t) = \sum_{n=0}^\infty \dim(R_n) t^n \) | Modular form or series \( \Theta(q) = \sum_{x \in L} q^{\|x\|^2} \) |
| Purpose | Tracks growth of graded components' dimensions | Enumerates lattice vectors by length squared |
| Typical Use | Commutative algebra, algebraic geometry, invariant theory | Number theory, modular forms, coding theory, sphere packings |
| Analytic Properties | Rational function under favorable conditions | Transforms like modular forms under group actions |
| Example | Hilbert series of polynomial ring \(k[x_1,...,x_n]\) is \(\frac{1}{(1-t)^n}\) | Theta series of integer lattice \( \mathbb{Z}^n \): \(\sum_{m=0}^\infty r_n(m) q^m\) where \(r_n(m)\) counts representations of \(m\) as sum of squares |
Introduction to Hilbert Series and Theta Series
Hilbert series and Theta series serve distinct roles in algebra and number theory, with Hilbert series primarily used to encode the dimension growth of graded algebras and modules, capturing the algebraic structure through generating functions. Theta series, associated with quadratic forms and lattices, provide generating functions that enumerate representations of integers as sums of squares, linking number theory and modular forms. Both series offer rich insights: the Hilbert series reveals algebraic properties like dimension and depth, while the Theta series encodes arithmetic information and symmetry in lattice structures.
Mathematical Foundations of Hilbert Series
Hilbert series provide a generating function that encodes the dimension of graded components in a graded algebra, playing a fundamental role in commutative algebra and algebraic geometry. The mathematical foundation of Hilbert series relies on the structure of graded rings and modules, where the series captures growth rates and algebraic invariants through formal power series. Unlike Theta series, which arise in the study of quadratic forms and modular forms, Hilbert series focus primarily on the combinatorial and homological properties of algebraic objects.
Mathematical Background of Theta Series
Theta series arise from the study of quadratic forms and lattices, representing generating functions that encode the number of lattice points at given norms through q-series expansions. These series connect deeply to modular forms, revealing symmetries in the distribution of lattice points and enabling the analysis of arithmetic properties. Hilbert series, in contrast, typically enumerate graded dimensions of algebraic structures, while theta series emphasize geometric and number-theoretic aspects intrinsic to quadratic lattices.
Key Differences Between Hilbert and Theta Series
Hilbert series encode the dimension of graded components of graded algebras, providing algebraic information about growth rates, while Theta series capture lattice point enumerations weighted by quadratic forms, reflecting geometric and number-theoretic properties. Hilbert series are rational functions typically used in commutative algebra and algebraic geometry, whereas Theta series are modular forms arising in the theory of quadratic forms and modular functions. The main difference lies in their applications: Hilbert series analyze algebraic structures' grading, while Theta series study arithmetic and geometric properties of lattices.
Applications of Hilbert Series in Algebra and Geometry
Hilbert series serve as powerful tools in algebra and geometry by encoding the dimension growth of graded components in graded algebras, crucial for understanding the structure of polynomial rings and modules. They facilitate the computation of invariants in projective varieties, helping to determine geometric properties such as dimension and degree through the study of Hilbert polynomials derived from the series. Unlike Theta series, which are primarily used in the study of lattices and modular forms, Hilbert series provide essential insights into syzygies, resolutions, and the algebraic underpinnings of geometric objects.
Applications of Theta Series in Number Theory
Theta series serve as generating functions encoding representations of integers by quadratic forms, making them essential tools in number theory for studying lattice point distributions and modular forms. Their applications extend to counting solutions of Diophantine equations, analyzing quadratic forms classification, and exploring connections with elliptic curves and modularity theorems. Hilbert series, primarily used in commutative algebra and algebraic geometry to study graded algebras, contrast with theta series by focusing on dimension counting rather than arithmetic properties of forms.
Hilbert Series: Computation and Examples
Hilbert series provide a generating function that encodes the dimension of graded components in graded algebras, essential for understanding algebraic structures in commutative algebra and algebraic geometry. The computation typically involves expressing the Hilbert series as a rational function derived from a minimal graded free resolution or by utilizing combinatorial techniques such as counting monomial bases. Examples include calculating the Hilbert series of polynomial rings, monomial ideals, or quotient rings, which reveal key invariants like the Krull dimension and Hilbert polynomial.
Theta Series: Computation and Examples
Theta series encode the number of lattice points in quadratic forms, serving as generating functions with coefficients representing the counts of vectors of fixed norm. Their computation often involves sums over lattice points or modular forms, utilizing algorithms such as the modular recursion or kernel methods to efficiently handle high-dimensional cases. Examples include the theta series of the integer lattice \(\mathbb{Z}^n\), which corresponds to classical theta functions, and those of root lattices like \(E_8\), illuminating deep connections between lattice theory and modular forms.
Interconnections Between Hilbert and Theta Series
Hilbert series encode the dimension growth of graded components in algebraic structures, particularly in graded rings and modules, while theta series capture the distribution of quadratic forms or lattice points and serve as generating functions in number theory and geometry. The interconnections between Hilbert and theta series arise prominently in the study of modular forms and algebraic geometry, where theta series often provide explicit realizations or generating functions for special classes of Hilbert series associated with lattice-based algebras or graded rings constructed from quadratic forms. This relationship enables the transfer of analytic properties and modular invariance from theta series to the combinatorial and algebraic information encoded by Hilbert series, enriching the understanding of both invariants in representation theory and arithmetic geometry.
Conclusion: Choosing Between Hilbert and Theta Series
Hilbert series provide a concise algebraic tool to study graded rings and modules by encoding dimension data of graded components, making them ideal for algebraic geometry and commutative algebra applications. Theta series serve to encode lattice point distributions and modular form properties, crucial in number theory and coding theory. Choosing between Hilbert and Theta series depends on whether the focus lies on algebraic structure and dimension (favor Hilbert) or on arithmetic properties of lattices and modularity (favor Theta).
Hilbert series Infographic
 libterm.com
libterm.com