Exact sequence analysis plays a crucial role in understanding genetic information and identifying mutations within DNA strands. By examining these precise arrangements of nucleotides, researchers can uncover critical insights into hereditary diseases and evolutionary biology. Explore the rest of this article to learn how exact sequence techniques can impact your understanding of genetics.
Table of Comparison
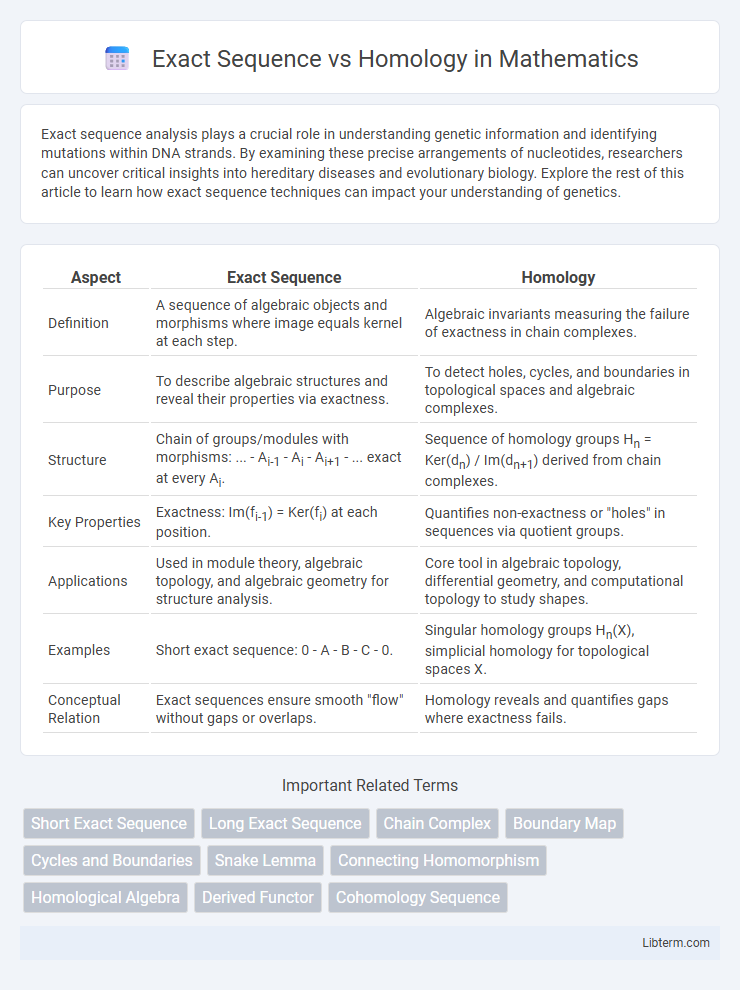
| Aspect | Exact Sequence | Homology |
|---|---|---|
| Definition | A sequence of algebraic objects and morphisms where image equals kernel at each step. | Algebraic invariants measuring the failure of exactness in chain complexes. |
| Purpose | To describe algebraic structures and reveal their properties via exactness. | To detect holes, cycles, and boundaries in topological spaces and algebraic complexes. |
| Structure | Chain of groups/modules with morphisms: ... - Ai-1 - Ai - Ai+1 - ... exact at every Ai. | Sequence of homology groups Hn = Ker(dn) / Im(dn+1) derived from chain complexes. |
| Key Properties | Exactness: Im(fi-1) = Ker(fi) at each position. | Quantifies non-exactness or "holes" in sequences via quotient groups. |
| Applications | Used in module theory, algebraic topology, and algebraic geometry for structure analysis. | Core tool in algebraic topology, differential geometry, and computational topology to study shapes. |
| Examples | Short exact sequence: 0 - A - B - C - 0. | Singular homology groups Hn(X), simplicial homology for topological spaces X. |
| Conceptual Relation | Exact sequences ensure smooth "flow" without gaps or overlaps. | Homology reveals and quantifies gaps where exactness fails. |
Introduction to Exact Sequences and Homology
Exact sequences in algebra provide a structured framework to analyze chains of algebraic objects and morphisms, ensuring that the image of one morphism equals the kernel of the next. Homology measures the failure of exactness in these sequences, capturing topological or algebraic invariants by quantifying cycles and boundaries within chain complexes. Together, exact sequences and homology form foundational tools in algebraic topology, homological algebra, and related fields for understanding and classifying complex structures.
Definitions: Exact Sequence Explained
Exact sequence refers to a sequence of algebraic objects and morphisms between them, where the image of one morphism precisely equals the kernel of the next, ensuring no loss of information at each step. Homology measures the failure of exactness, identifying elements that are mapped to zero but do not originate from the previous morphism, thus capturing topological or algebraic invariants. Understanding exact sequences is fundamental in fields like algebraic topology and homological algebra for analyzing the structure and relationships of mathematical objects.
Understanding Homology in Algebraic Topology
Homology in algebraic topology studies topological spaces by analyzing cycles and boundaries within chain complexes to classify features like holes of various dimensions. Exact sequences provide a framework to relate homology groups of different spaces or pairs through sequences of homomorphisms, revealing how these groups fit together algebraically. Understanding homology entails interpreting these exact sequences to track how topological features persist or disappear across spaces and maps.
Key Differences: Exact Sequence vs Homology
Exact sequence comparison identifies 100% nucleotide or amino acid identity between two sequences, ensuring no variation in the aligned region. Homology refers to the evolutionary relationship between sequences, indicating a common ancestor, even if similarity is less than 100%. Exact sequence analysis is quantitative and precise, while homology is qualitative and inferential, often requiring bioinformatics tools like BLAST to assess evolutionary connections.
The Role of Exact Sequences in Homological Algebra
Exact sequences serve as fundamental tools in homological algebra by providing a structured framework to analyze the relationships between algebraic objects such as modules, groups, or chain complexes. They allow mathematicians to track the flow of homomorphisms and identify kernels and images, thereby facilitating the computation of homology and cohomology groups. Through exact sequences, intricate properties of algebraic structures emerge, enabling deeper insights into extensions, resolutions, and derived functors within homological contexts.
Homology Groups: Computation and Significance
Homology groups provide a fundamental algebraic tool for measuring topological spaces' features by classifying cycles and boundaries into equivalence classes. Their computation involves constructing chain complexes from simplicial or singular chains, followed by calculating the quotient of cycles modulo boundaries to identify invariants like Betti numbers. These groups signify critical topological properties such as connectivity, the presence of holes, and higher-dimensional voids, which are instrumental in fields like algebraic topology, persistent homology in data analysis, and manifold theory.
Examples: Exact Sequences in Practice
Exact sequences in algebra provide a framework to analyze the structure of modules by representing precise relationships between kernels and images of homomorphisms, with common examples including short exact sequences like 0 - A - B - C - 0 that characterize extensions of modules. In homological algebra, exact sequences elucidate properties of chain complexes, illustrated by the long exact sequence in homology derived from a short exact sequence of chain complexes, which reveals intricate connections between homology groups. These practical instances demonstrate how exact sequences serve as essential tools for identifying invariants and understanding morphisms beyond mere homological similarity or homology group isomorphisms.
Relationship Between Exact Sequences and Homology
Exact sequences provide a framework to analyze homology groups in algebraic topology by connecting chains, cycles, and boundaries through a sequence of homomorphisms. The relationship is fundamental as exactness at each stage implies that the image of one map equals the kernel of the next, thereby detecting homological features like holes or voids in topological spaces. This interplay enables computation of homology groups by decomposing complex spaces into simpler components whose homological properties are linked via exact sequences.
Applications in Mathematics and Beyond
Exact sequences in mathematics provide a structured framework to analyze algebraic objects by capturing their relationships through a chain of morphisms, enabling precise computations in homological algebra and topology. Homology, derived from exact sequences, offers powerful tools for classifying topological spaces and studying algebraic invariants, with applications extending to data analysis, robotics, and physics. Both concepts facilitate deep insights into the connectivity and structure of complex systems, essential for advancements in abstract algebra, category theory, and applied computational methods.
Conclusion: Choosing Between Exact Sequence and Homology
Choosing between exact sequence matching and homology depends on the research objective and data specificity. Exact sequence matching excels in identifying precise genetic variants and mutations, while homology is more effective for inferring functional and evolutionary relationships across different species. Researchers should prioritize exact sequence analysis for pinpoint accuracy and rely on homology-based methods for broader comparative genomics and functional annotation tasks.
Exact Sequence Infographic
 libterm.com
libterm.com