A universal cover is a fundamental concept in topology that provides a simply connected space mapping onto a given topological space, effectively unraveling its loops and twists. This construction helps analyze complex spaces by lifting paths and homotopies, making it essential in algebraic topology and geometric group theory. Discover how universal covers reveal hidden structures and simplify your understanding in the rest of this article.
Table of Comparison
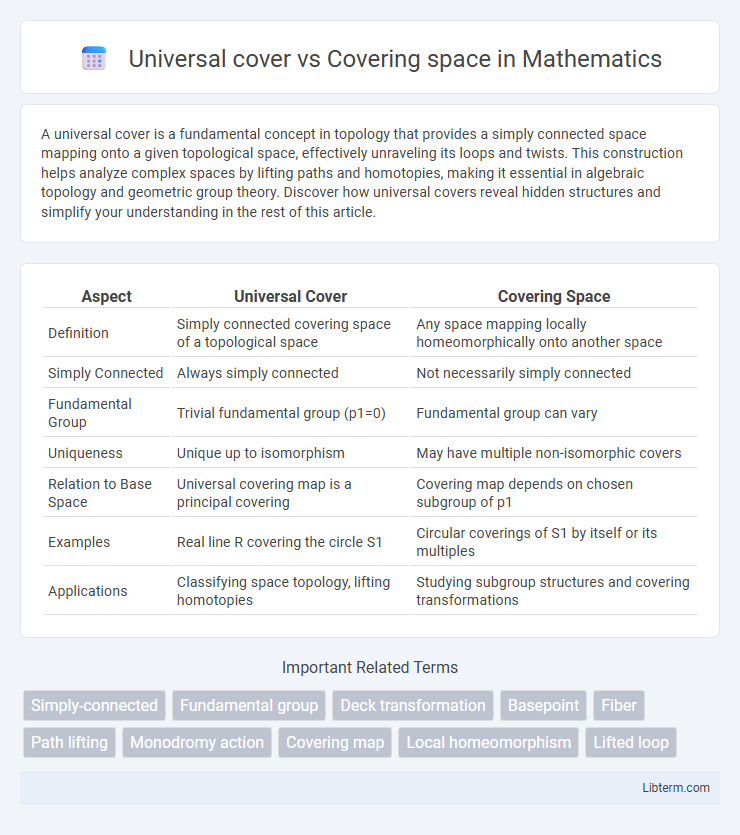
| Aspect | Universal Cover | Covering Space |
|---|---|---|
| Definition | Simply connected covering space of a topological space | Any space mapping locally homeomorphically onto another space |
| Simply Connected | Always simply connected | Not necessarily simply connected |
| Fundamental Group | Trivial fundamental group (p1=0) | Fundamental group can vary |
| Uniqueness | Unique up to isomorphism | May have multiple non-isomorphic covers |
| Relation to Base Space | Universal covering map is a principal covering | Covering map depends on chosen subgroup of p1 |
| Examples | Real line R covering the circle S1 | Circular coverings of S1 by itself or its multiples |
| Applications | Classifying space topology, lifting homotopies | Studying subgroup structures and covering transformations |
Introduction to Universal Covers and Covering Spaces
Universal covers are special types of covering spaces characterized by their simply connected nature, meaning they have no nontrivial loops. Covering spaces map onto a base space such that locally around every point, the map resembles a homeomorphism, allowing for the study of complex spaces via simpler, well-understood structures. In topology, universal covers serve as the most extensive covering space from which all other coverings of the base space can be derived through quotienting by subgroups of the fundamental group.
Fundamental Concepts in Topology
A universal cover is a specific type of covering space that is simply connected, meaning it has no nontrivial loops, making it a crucial concept in algebraic topology. Covering spaces generally consist of a continuous surjective map from a topological space onto another, locally resembling a projection, and are used to study the properties of the base space through its fibers. The universal cover serves as the largest covering space, factoring through all other connected covering spaces, and fundamentally links to the fundamental group by providing a space where this group acts as the deck transformation group.
Definition of Covering Space
A covering space is a topological space \( \tilde{X} \) equipped with a continuous surjective map \( p: \tilde{X} \to X \) such that for every point \( x \in X \), there exists an open neighborhood \( U \subseteq X \) where \( p^{-1}(U) \) is a disjoint union of open sets in \( \tilde{X} \), each homeomorphic to \( U \) via \( p \). This local homeomorphism property ensures that the covering map \( p \) "locally looks like" a projection from multiple copies of \( U \) onto \( U \). Universal covers are special cases of covering spaces where \( \tilde{X} \) is simply connected, serving as a maximal covering space that covers every other covering space of \( X \).
Understanding Universal Covers
Universal covers serve as a specialized type of covering space characterized by simply connected total spaces, providing a unique and maximal covering for a given topological space. Understanding universal covers involves recognizing their role in lifting paths and homotopies, which simplifies the study of fundamental groups by converting complex loop structures into trivial ones. This concept is essential in algebraic topology, enabling the classification of covering spaces through the fundamental group and facilitating the analysis of topological properties of spaces.
Key Differences Between Universal Covers and Covering Spaces
Universal covers are simply connected covering spaces that map onto a base space, serving as the maximal covering space with a trivial fundamental group. Covering spaces may have nontrivial fundamental groups, and they correspond to subgroups of the base space's fundamental group, reflecting various degrees of connectedness. The key difference lies in universal covers being unique up to isomorphism and providing a systematic way to study the topology of spaces via their fundamental group, while general covering spaces represent broader classes of topological coverings without the requirement of simple connectivity.
Construction Methods for Universal Covers
Universal covers are constructed by examining the fundamental group of a topological space and building a simply connected space that maps onto the original via a covering map. Techniques often involve lifting paths and homotopies, utilizing the path space or deck transformations to systematically unfold loops. In contrast, general covering spaces may not be simply connected and their construction depends on subgroups of the fundamental group, allowing for a broader range of coverings than the universal cover.
Examples of Covering Spaces and Universal Covers
Examples of covering spaces include the circle S1 covered by the real line R through the exponential map, illustrating a universal cover since R is simply connected. A non-universal covering space example is the torus T2 covered by the cylinder S1 x R, which is not simply connected and thus not universal. Universal covers serve as foundational tools in algebraic topology by providing simply connected covering spaces that reveal fundamental group structures of complex spaces.
Applications in Algebraic Topology
Universal covers serve as principal tools in algebraic topology by providing simply connected covering spaces that simplify the study of fundamental groups and homotopy types. Covering spaces more generally enable classification of spaces via group actions, facilitating computations of invariants like the fundamental group and homology groups. Applications include lifting properties for maps, analyzing fiber bundles, and solving extension problems in homotopy theory.
Importance in Fundamental Group Analysis
Universal covers serve as key tools in fundamental group analysis by providing simply connected covering spaces that reveal the structure of the base space's fundamental group. Covering spaces correspond to subgroups of the fundamental group, allowing classification and by investigating universal covers, one obtains insights into the group's generators and relations. The universal cover's uniqueness and existence for path-connected, locally path-connected, and semi-locally simply connected spaces make it essential for algebraic topology and group theory applications.
Summary and Key Takeaways
Universal cover is a special type of covering space characterized by being simply connected, meaning it contains no nontrivial loops. Every covering space can be derived from the universal cover via a group action of the fundamental group of the base space. The universal cover serves as a foundational tool in algebraic topology for analyzing topological spaces through their fundamental groups and covering spaces.
Universal cover Infographic
 libterm.com
libterm.com