Invariant properties remain constant regardless of changes in other variables or conditions, providing stability in mathematical, physical, and computational contexts. Understanding these unchanging elements is crucial for solving complex problems and ensuring consistency in your analyses or algorithms. Explore the rest of this article to discover how invariants can simplify challenges across diverse fields.
Table of Comparison
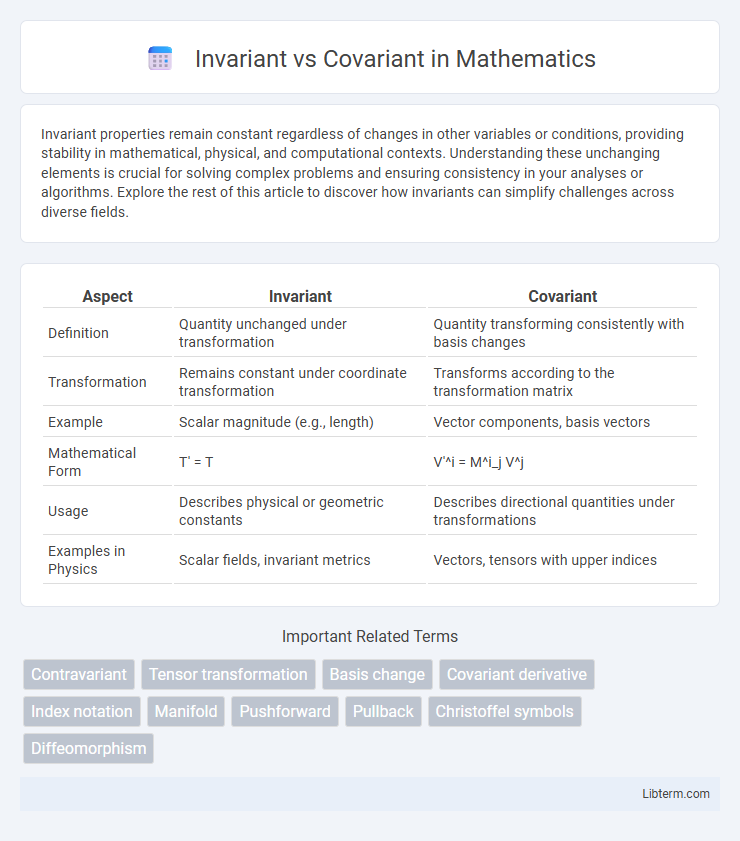
| Aspect | Invariant | Covariant |
|---|---|---|
| Definition | Quantity unchanged under transformation | Quantity transforming consistently with basis changes |
| Transformation | Remains constant under coordinate transformation | Transforms according to the transformation matrix |
| Example | Scalar magnitude (e.g., length) | Vector components, basis vectors |
| Mathematical Form | T' = T | V'^i = M^i_j V^j |
| Usage | Describes physical or geometric constants | Describes directional quantities under transformations |
| Examples in Physics | Scalar fields, invariant metrics | Vectors, tensors with upper indices |
Introduction to Invariant and Covariant Concepts
Invariant types require exact type matches, meaning an object of one type cannot be substituted with another, even if they share a hierarchy. Covariant types allow a subtype to be substituted where a supertype is expected, preserving type safety in return types. Understanding invariant and covariant concepts is essential in programming languages to manage type compatibility and ensure code reliability.
Defining Invariance in Mathematics and Physics
Invariance in mathematics and physics refers to a property of a system or equation that remains unchanged under a set of transformations or operations. Invariant quantities, such as scalar values or norms, preserve their form regardless of coordinate changes, enabling consistent descriptions across different reference frames. This concept contrasts with covariance, where objects transform systematically but maintain relationships defined by underlying symmetry groups.
Understanding Covariance: A Semantic Overview
Covariance refers to the ability of a type system to preserve the subtype relationship when types are used in a more complex structure, such as generic collections or function return types. In programming languages like Scala and C#, covariance allows a type like List
Key Differences Between Invariant and Covariant
Invariant types require exact matches, ensuring type safety by preventing substitution with derived or base types, which reduces flexibility but increases predictability. Covariant types allow a type to be substituted with its derived type, enabling more flexible and reusable code, especially in output or return types like arrays or collections. The key difference lies in assignment compatibility: invariance denies subtype substitution, while covariance permits it when preserving type relationships in inheritance hierarchies.
Practical Examples of Invariance
Invariance in programming ensures type safety by disallowing type substitution between generic types, such as List
Real-World Applications of Covariance
Covariance plays a crucial role in real-world applications such as type-safe collections in programming languages like Java and C#, enabling flexibility in assigning and passing generic types while preserving type safety. In software development, covariance allows for method overriding and interface implementation where return types can be more derived, facilitating polymorphism and code reuse. Additionally, covariance is essential in data modeling and serialization frameworks, ensuring consistent handling of subtype instances without compromising data integrity.
Invariance vs Covariance in Linear Algebra
In linear algebra, invariance refers to the property of a vector or subspace remaining unchanged under a linear transformation, signifying consistency across different bases. Covariance describes how components of a vector transform in a correlating manner with the basis change, specifically following the transformation matrix directly. Understanding invariance versus covariance is crucial for analyzing how geometric objects and coordinate representations behave under linear maps and basis transformations.
Invariant and Covariant in Machine Learning
Invariant features in machine learning refer to representations that remain unchanged under specific transformations such as rotation, scaling, or translation, enhancing model robustness by focusing on essential patterns rather than superficial variations. Covariant features, conversely, change predictably with transformations, allowing models to adapt outputs based on input variations, which is crucial in tasks like object detection where positional information matters. Understanding the balance between invariance and covariance improves model design for tasks demanding stability or sensitivity to changes in data representation.
Common Misconceptions and Clarifications
Invariant types neither accept subtypes nor supertypes of the specified generic type, ensuring strict type safety but limiting flexibility. Covariant types allow substitution with more derived (subtype) generic types, enhancing reusability but sometimes causing unintended runtime exceptions if not handled carefully. A common misconception is that covariance always preserves type safety; however, covariance is safe only in output scenarios, such as return types, while input positions require invariance or contravariance to prevent type errors.
Summary: Choosing Between Inariant and Covariant
Choosing between invariant and covariant types hinges on the desired flexibility and type safety in programming languages. Invariant types enforce exact type matches, ensuring strict type consistency but limiting subtype substitutability, whereas covariant types allow subtype variations, enhancing code reusability and polymorphism. The decision depends on balancing the needs for rigid type control against the benefits of flexible subtype compatibility in type hierarchies.
Invariant Infographic
 libterm.com
libterm.com