A symplectic manifold is a smooth even-dimensional space equipped with a closed, non-degenerate 2-form called a symplectic form, which enables the study of geometry and dynamics in classical mechanics. This structure provides a natural framework for Hamiltonian systems, allowing you to analyze phase space and conservation laws effectively. Explore the rest of the article to understand how symplectic manifolds underpin modern mathematical physics and geometry.
Table of Comparison
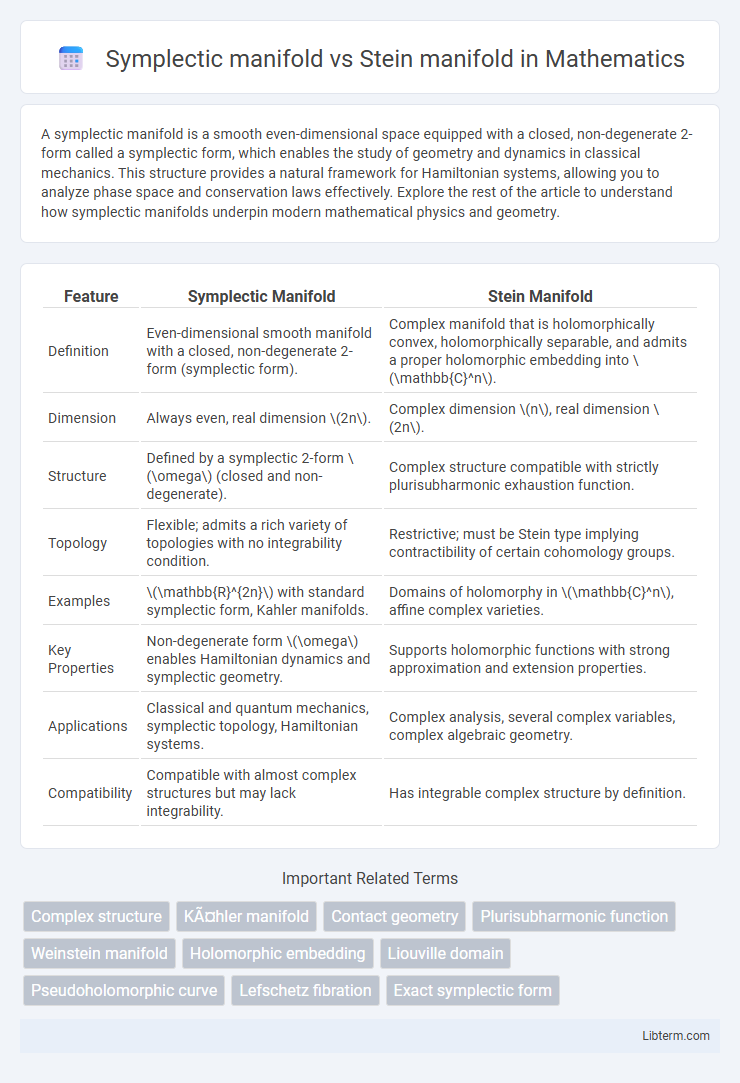
| Feature | Symplectic Manifold | Stein Manifold |
|---|---|---|
| Definition | Even-dimensional smooth manifold with a closed, non-degenerate 2-form (symplectic form). | Complex manifold that is holomorphically convex, holomorphically separable, and admits a proper holomorphic embedding into \(\mathbb{C}^n\). |
| Dimension | Always even, real dimension \(2n\). | Complex dimension \(n\), real dimension \(2n\). |
| Structure | Defined by a symplectic 2-form \(\omega\) (closed and non-degenerate). | Complex structure compatible with strictly plurisubharmonic exhaustion function. |
| Topology | Flexible; admits a rich variety of topologies with no integrability condition. | Restrictive; must be Stein type implying contractibility of certain cohomology groups. |
| Examples | \(\mathbb{R}^{2n}\) with standard symplectic form, Kahler manifolds. | Domains of holomorphy in \(\mathbb{C}^n\), affine complex varieties. |
| Key Properties | Non-degenerate form \(\omega\) enables Hamiltonian dynamics and symplectic geometry. | Supports holomorphic functions with strong approximation and extension properties. |
| Applications | Classical and quantum mechanics, symplectic topology, Hamiltonian systems. | Complex analysis, several complex variables, complex algebraic geometry. |
| Compatibility | Compatible with almost complex structures but may lack integrability. | Has integrable complex structure by definition. |
Introduction to Symplectic and Stein Manifolds
Symplectic manifolds are smooth even-dimensional spaces equipped with a closed, non-degenerate 2-form that provides a framework for classical mechanics and geometric analysis. Stein manifolds, arising in complex analysis, are complex manifolds characterized by holomorphic convexity and the existence of plenty of global holomorphic functions, serving as the complex analogs of affine varieties. While symplectic manifolds emphasize differential forms and smooth structures, Stein manifolds focus on complex structures and holomorphic function theory, highlighting their distinct roles in geometry and analysis.
Defining Symplectic Manifolds: Core Concepts
Symplectic manifolds are smooth, even-dimensional manifolds equipped with a closed, non-degenerate 2-form called the symplectic form, which provides a geometric framework for classical mechanics and Hamiltonian dynamics. This non-degeneracy condition implies the existence of a rich structure, allowing for the identification of canonical coordinates and facilitating the study of phase spaces. In contrast, Stein manifolds arise in complex analysis as complex manifolds that admit proper holomorphic embeddings into complex Euclidean space, emphasizing complex structure rather than the symplectic form central to symplectic geometry.
Key Properties of Stein Manifolds
Stein manifolds are complex manifolds characterized by their holomorphic convexity, existence of plenty of global holomorphic functions, and property of being holomorphically embeddable into complex Euclidean spaces. These manifolds exhibit important cohomological properties, including vanishing higher cohomology groups for coherent analytic sheaves, which distinguishes them from general complex or symplectic manifolds. Symplectic manifolds, defined by a closed non-degenerate 2-form, focus on geometric structures related to Hamiltonian dynamics and lack the strong analytic function theory that defines Stein manifolds.
Historical Development and Mathematical Context
Symplectic manifolds emerged from classical mechanics in the 19th century, formalized through the work of Hamilton and Poincare, providing a geometric framework for phase spaces in physics. Stein manifolds, introduced by Karl Stein in the 1950s, arose in complex analysis as a generalization of domains of holomorphy, playing a crucial role in several complex variables and complex geometry. The development of symplectic geometry intertwined with differential topology and dynamical systems, whereas Stein manifolds contributed significantly to the study of complex structures and analytic function theory.
Topological Differences: Symplectic vs Stein
Symplectic manifolds are even-dimensional smooth manifolds equipped with a closed, non-degenerate 2-form, which induces a rich geometric structure but imposes no strict restrictions on the underlying topology beyond even dimensionality and orientability. Stein manifolds, as complex-analytic analogs of affine varieties, require strict topological conditions such as being holomorphically convex, complex-analytic, and diffeomorphic to a handlebody of dimension less than or equal to the complex dimension, ensuring they admit strictly plurisubharmonic exhaustion functions. The fundamental topological distinction lies in Stein manifolds' compatibility with complex structures and strict convexity properties, contrasting with the broader, less restrictive topologies allowed for symplectic manifolds.
Complex and Real Structures: A Comparative Overview
Symplectic manifolds are smooth real manifolds equipped with a closed, non-degenerate 2-form that defines a rich geometric structure crucial in classical and quantum mechanics. Stein manifolds, complex analytic analogues of affine spaces, are complex manifolds characterized by the existence of strictly plurisubharmonic exhaustion functions and holomorphic convexity. While symplectic manifolds emphasize real differentiable structures with symplectic forms, Stein manifolds focus on complex structures facilitating embedding into complex Euclidean space, revealing fundamental distinctions in their geometric and analytic properties.
Dimensional Constraints and Examples
Symplectic manifolds have even dimensions, typically \(2n\), equipped with a closed, non-degenerate 2-form, such as \(\mathbb{R}^{2n}\) with the standard symplectic structure. Stein manifolds, complex analytic and holomorphically convex, exist only in even real dimensions \(2n\) as complex \(n\)-dimensional manifolds, frequently exemplified by domains in \(\mathbb{C}^n\). While every Stein manifold admits a compatible symplectic structure, the dimensional constraint and geometric properties distinguish the symplectic category from the strictly complex-analytic Stein framework.
Embedding and Flexibility Properties
Symplectic manifolds exhibit rigidity in embedding due to Gromov's non-squeezing theorem, restricting symplectic embeddings and preserving symplectic structures under strict conditions. Stein manifolds, as complex manifolds with strictly plurisubharmonic exhaustion functions, allow flexible holomorphic embeddings into complex Euclidean spaces, facilitating intricate complex analytic structures. The contrast highlights symplectic manifolds' limited flexibility in embeddings versus Stein manifolds' rich capacity for complex embeddings and deformations.
Applications in Modern Mathematics
Symplectic manifolds play a crucial role in modern mathematical physics, particularly in Hamiltonian mechanics and string theory, as they provide the geometric framework for phase space analysis and integrable systems. Stein manifolds are central to complex analysis and several complex variables, serving as natural domains for holomorphic functions and facilitating the study of complex structures and embeddings. Their interplay enhances understanding in areas such as mirror symmetry, where symplectic geometry and complex analytic methods converge to solve problems in algebraic geometry and theoretical physics.
Open Problems and Future Directions
Open problems in symplectic and Stein manifolds revolve around classification challenges and the interplay between their geometric structures. Understanding how symplectic topology influences complex analytic properties in Stein manifolds remains a key research direction. Future studies aim to explore the existence of exotic structures and investigate symplectic invariants that could unify these manifold classes under broader geometric frameworks.
Symplectic manifold Infographic
 libterm.com
libterm.com