Coequalizers play a crucial role in category theory by providing a universal solution to the problem of equating two morphisms. They allow you to identify and merge elements in a structured way, ensuring consistency across related mathematical objects. Explore the rest of this article to understand how coequalizers function and their applications in various mathematical contexts.
Table of Comparison
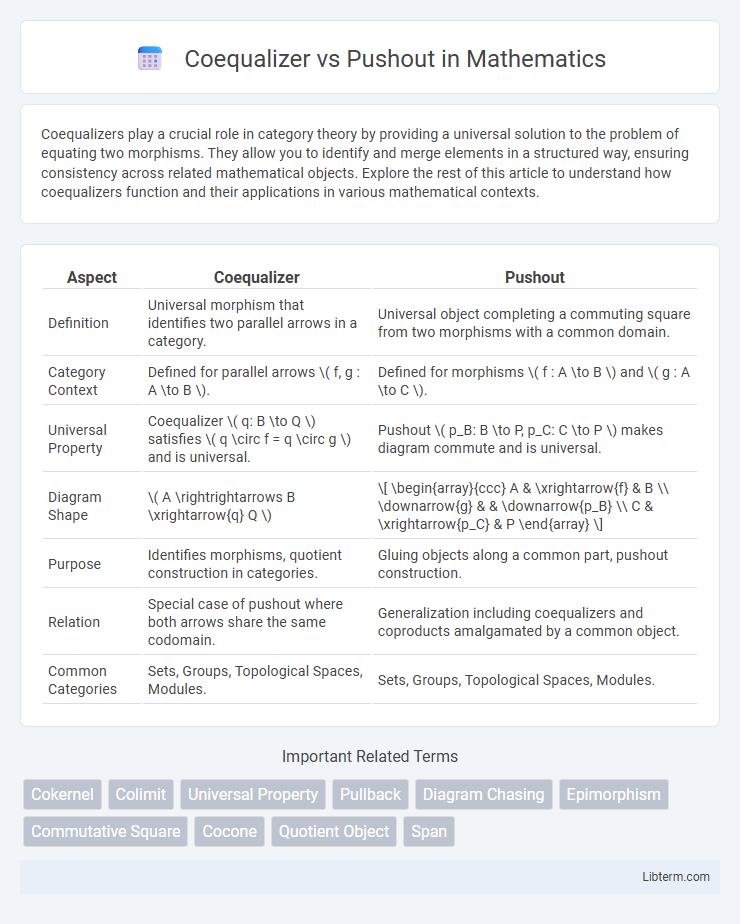
| Aspect | Coequalizer | Pushout |
|---|---|---|
| Definition | Universal morphism that identifies two parallel arrows in a category. | Universal object completing a commuting square from two morphisms with a common domain. |
| Category Context | Defined for parallel arrows \( f, g : A \to B \). | Defined for morphisms \( f : A \to B \) and \( g : A \to C \). |
| Universal Property | Coequalizer \( q: B \to Q \) satisfies \( q \circ f = q \circ g \) and is universal. | Pushout \( p_B: B \to P, p_C: C \to P \) makes diagram commute and is universal. |
| Diagram Shape | \( A \rightrightarrows B \xrightarrow{q} Q \) | \[ \begin{array}{ccc} A & \xrightarrow{f} & B \\ \downarrow{g} & & \downarrow{p_B} \\ C & \xrightarrow{p_C} & P \end{array} \] |
| Purpose | Identifies morphisms, quotient construction in categories. | Gluing objects along a common part, pushout construction. |
| Relation | Special case of pushout where both arrows share the same codomain. | Generalization including coequalizers and coproducts amalgamated by a common object. |
| Common Categories | Sets, Groups, Topological Spaces, Modules. | Sets, Groups, Topological Spaces, Modules. |
Introduction to Coequalizer and Pushout
Coequalizers and pushouts are fundamental constructions in category theory used to identify and merge objects based on morphisms. A coequalizer is a universal morphism that equates two parallel arrows, effectively creating a quotient object that identifies elements related by the morphisms. Pushouts generalize this notion by combining two objects with a shared subobject, forming a colimit that unifies structures along a common part, crucial for gluing diagrams and modelling amalgamations in various mathematical contexts.
Fundamental Concepts in Category Theory
Coequalizer and pushout are fundamental constructions in category theory that generalize notions of quotient and gluing, respectively. A coequalizer captures the universal property of identifying morphisms with the same codomain, effectively modeling equivalence relations and quotient objects. Pushouts represent the categorical dual of pullbacks, combining two objects along a common subobject to form a universal "gluing" object, crucial for colimits and diagram completions.
What is a Coequalizer?
A coequalizer in category theory is a universal construction that identifies and merges morphisms by factoring out their equivalence relation, effectively creating the "largest quotient" that equalizes two parallel arrows. It serves as a canonical solution to the problem of making two morphisms equal by mapping from their common codomain to a target object. Unlike a pushout, which combines objects along a shared subobject, the coequalizer specifically addresses the collapse of morphism differences into a single morphism.
What is a Pushout?
A pushout is a categorical construction that represents the colimit of two morphisms with a common domain, effectively "gluing" objects together along shared structure. It generalizes the union of sets and serves as a fundamental concept in algebraic topology, category theory, and computer science for combining spaces, types, or data structures. Pushouts uniquely characterize the minimal object into which two given objects map while preserving their identified parts.
Diagrammatic Representations
Coequalizers and pushouts are fundamental constructions in category theory used to identify and glue objects via morphisms. A coequalizer diagram typically consists of two parallel arrows \( f, g: A \to B \) with a morphism \( q: B \to Q \) such that \( q \circ f = q \circ g \), capturing the universal property of identifying elements equated by \( f \) and \( g \). In contrast, a pushout diagram involves a span \( A \xrightarrow{f} B \) and \( A \xrightarrow{g} C \), with universal morphisms \( B \to P \) and \( C \to P \) that coalesce the two morphisms into a commutative square, visually representing the amalgamation along \( A \).
Key Differences: Coequalizer vs Pushout
Coequalizers identify and merge elements under a given pair of parallel morphisms in category theory, producing a universal target object that equalizes these morphisms. Pushouts, in contrast, unify two objects along a common subobject by forming a universal cocone, effectively gluing objects via a shared morphism. The key difference lies in construction: coequalizers resolve morphism equality conditions, while pushouts amalgamate objects over an intersection, influencing how colimits are computed in categorical contexts.
Applications in Mathematics and Computer Science
Coequalizers and pushouts serve distinct roles in category theory with critical applications in mathematics and computer science. Coequalizers generalize quotient structures by identifying morphisms, which is essential in algebra for constructing quotient groups and modules, and in computer science for modeling state machine minimization and process equivalence. Pushouts, as colimits combining diagrams via shared subobjects, underpin constructions in topology, such as glueing spaces, and in computer science, facilitate modular system design, type theory, and database schema integration.
Examples Illustrating Coequalizer and Pushout
Coequalizers in category theory can be illustrated by identifying elements in sets, such as merging two functions \(f, g: A \to B\) by equating their outputs, for example, coequalizing the parallel arrows from two copies of a set \(A\) into \(B\). Pushouts represent the universal construction for gluing two objects along a common subobject, exemplified by the pushout in the category of sets where two sets \(B\) and \(C\) are joined along a shared subset \(A\) to form a disjoint union with identified elements. Concrete examples include forming quotient groups using coequalizers and constructing topological spaces by attaching along a subspace, demonstrating the practical differences and similarities in these colimit concepts.
Choosing Between Coequalizer and Pushout
Choosing between a coequalizer and a pushout depends on the specific categorical construction needed: coequalizers specialize in identifying equivalence relations by merging parallel morphisms, while pushouts generalize this by combining objects along a shared subobject. In contexts requiring the quotient of morphisms to enforce identifications, coequalizers provide the minimal universal solution. Pushouts serve broader purposes in gluing diagrams or constructing colimits in categories, making them suitable for unifying objects with morphisms that share a common domain.
Conclusion and Further Reading
Coequalizer and pushout are both categorical constructs used to identify common equivalence relations and merge diagrams in category theory, with the coequalizer specifically focusing on equalizing parallel morphisms and the pushout amalgamating two objects over a shared subobject. The pushout generalizes the coequalizer by handling more complex diagrams, making it essential in fields like algebraic topology, homological algebra, and diagrammatic reasoning. For further exploration, consult "Categories for the Working Mathematician" by Saunders Mac Lane and research articles on colimits in category theory to deepen understanding of these fundamental concepts.
Coequalizer Infographic
 libterm.com
libterm.com