Strong connection drives meaningful relationships and enhances communication across all areas of life. Building and maintaining these connections requires intentional effort, empathy, and consistent interaction. Discover how you can strengthen your connections and unlock their full potential by reading the rest of this article.
Table of Comparison
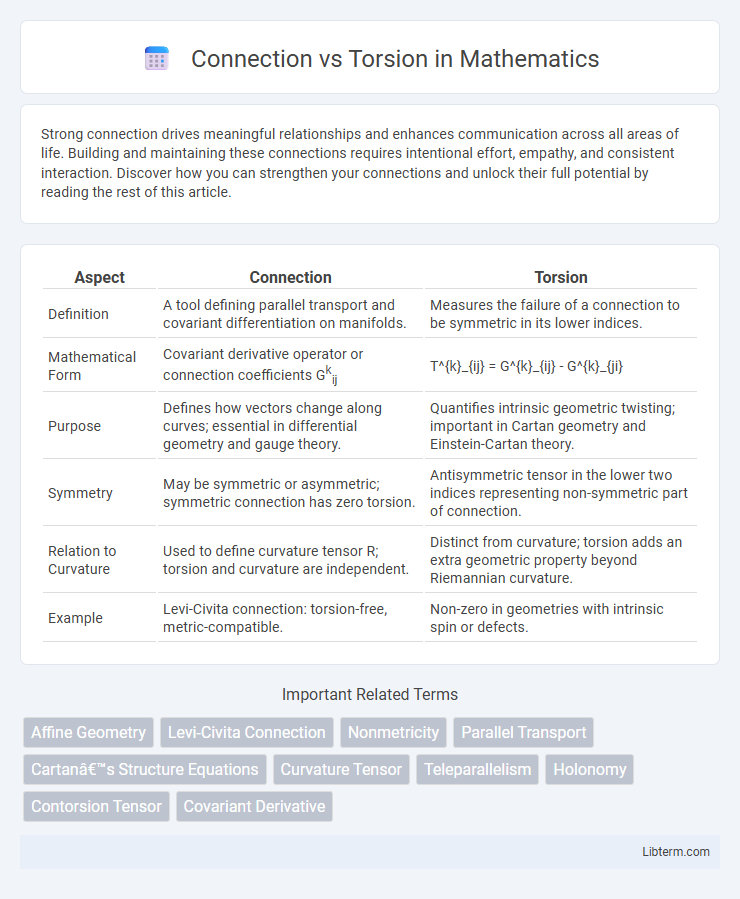
| Aspect | Connection | Torsion |
|---|---|---|
| Definition | A tool defining parallel transport and covariant differentiation on manifolds. | Measures the failure of a connection to be symmetric in its lower indices. |
| Mathematical Form | Covariant derivative operator or connection coefficients Gkij | T^{k}_{ij} = G^{k}_{ij} - G^{k}_{ji} |
| Purpose | Defines how vectors change along curves; essential in differential geometry and gauge theory. | Quantifies intrinsic geometric twisting; important in Cartan geometry and Einstein-Cartan theory. |
| Symmetry | May be symmetric or asymmetric; symmetric connection has zero torsion. | Antisymmetric tensor in the lower two indices representing non-symmetric part of connection. |
| Relation to Curvature | Used to define curvature tensor R; torsion and curvature are independent. | Distinct from curvature; torsion adds an extra geometric property beyond Riemannian curvature. |
| Example | Levi-Civita connection: torsion-free, metric-compatible. | Non-zero in geometries with intrinsic spin or defects. |
Understanding Connection and Torsion in Geometry
Connection and torsion are fundamental concepts in differential geometry that describe the properties of curves and manifolds. Connection defines how vectors are transported along a surface, enabling the measurement of how a curve bends, while torsion quantifies the rate at which a curve twists out of the plane of curvature. Understanding connection and torsion is essential for analyzing the intrinsic and extrinsic geometry of curves, impacting fields such as theoretical physics and engineering.
Core Differences Between Connection and Torsion
Connection defines how vectors are transported parallelly on a manifold, establishing a rule for differentiating vector fields along curves, while torsion measures the failure of the connection to be symmetric in its lower two indices, indicating the presence of an intrinsic "twisting" of the manifold. The core difference lies in their mathematical roles: connections enable the comparison of vectors at different points, integral to defining covariant derivatives, whereas torsion quantifies the antisymmetric part of the connection, often vanishing in Levi-Civita connections used in Riemannian geometry. Torsion's presence or absence directly affects the manifold's geometric and physical interpretations, such as in Einstein-Cartan theory, which extends general relativity by incorporating torsion to account for spin and intrinsic angular momentum.
Mathematical Foundations of Connection
The mathematical foundations of connection involve defining a way to compare vectors in neighboring tangent spaces on a differentiable manifold, enabling differentiation of vector fields along curves. Connections are characterized by Christoffel symbols that encode how basis vectors change from point to point, providing the framework for parallel transport and covariant differentiation. Unlike torsion, which measures the failure of commutativity in covariant derivatives and captures the twisting of space, the connection itself establishes the rule for how vectors are transported and how curvature is formulated through curvature tensors.
Defining Torsion: Concepts and Significance
Torsion refers to the twisting of an object due to an applied torque or rotational force, causing shear stress over its cross-section. This mechanical phenomenon is critical in engineering for designing shafts, beams, and structural elements to ensure they withstand operational stresses without failure. Understanding torsion enables precise calculation of angular deformation and material strength, directly impacting safety and performance in construction and machinery.
The Role of Connection in Differential Geometry
Connection in differential geometry provides a systematic way to compare tangent spaces at different points on a manifold, enabling the definition of parallel transport and covariant differentiation. It encodes how vectors are transported along curves, preserving geometrical and physical properties essential for analyzing curvature and geodesics. While torsion measures the failure of the connection to be symmetric, the connection itself fundamentally governs the manifold's differential structure and curvature characteristics.
Implications of Torsion in Manifolds
Torsion in manifolds affects the geometric structure by introducing asymmetry in the connection, which deviates from the standard Levi-Civita connection that assumes zero torsion. This non-zero torsion impacts curvature properties, influencing parallel transport and geodesic behavior, and plays a critical role in fields such as Einstein-Cartan theory in gravitational physics. The presence of torsion modifies holonomy groups and affects topological invariants, thereby altering manifold characteristics and physical interpretations.
Connection vs Torsion: Impact on Curvature
Torsion modifies the connection in a manifold by introducing an antisymmetric component that affects parallel transport and geodesic deviation, altering curvature properties. Unlike the Levi-Civita connection, which is torsion-free and fully determined by the metric, connections with torsion can generate additional curvature terms linked to spin and intrinsic angular momentum in spacetime theories. The presence of torsion influences the Riemann curvature tensor, leading to modified gravitational dynamics in Einstein-Cartan and other gauge theories of gravity.
Common Applications in Physics and Engineering
Connection and torsion are critical concepts in physics and engineering, often analyzed in structural mechanics and material science. Connections refer to joints or interfaces linking components, essential in frameworks like bridges, buildings, and machinery, ensuring load transfer and stability. Torsion involves twisting of objects due to applied torque, crucial in shafts, beams, and drive systems, impacting stress distribution and angular displacement.
Examples Illustrating Connection and Torsion
Connection in differential geometry describes how vectors are parallel transported along curves on a manifold, illustrated by the Levi-Civita connection on a curved surface like a sphere, where tangent vectors rotate to maintain zero covariant derivative. Torsion measures the failure of the connection to be symmetric in its lower indices, as seen in the Weitzenbock connection used in teleparallel gravity, where torsion replaces curvature to describe gravitational effects. These examples highlight how connections preserve geometric structures while torsion captures intrinsic twisting, crucial in theories extending Riemannian geometry.
Summary: Connection and Torsion in Modern Mathematics
Connection in modern mathematics provides a systematic way to differentiate vectors along manifolds, facilitating the study of curvature and parallel transport. Torsion measures the failure of a connection to be symmetric, capturing intrinsic geometric twists not explained by curvature alone. Together, connection and torsion are fundamental in differential geometry and play critical roles in theories such as Einstein-Cartan gravity and gauge theories.
Connection Infographic
 libterm.com
libterm.com