Frame bundles play a crucial role in differential geometry by providing a structured way to study manifolds through collections of frames, or bases, attached to each tangent space. They enable the analysis of geometric and topological properties by linking local linear approximations to the manifold's global structure. Explore the rest of the article to understand how frame bundles impact manifold theory and their applications in modern geometry.
Table of Comparison
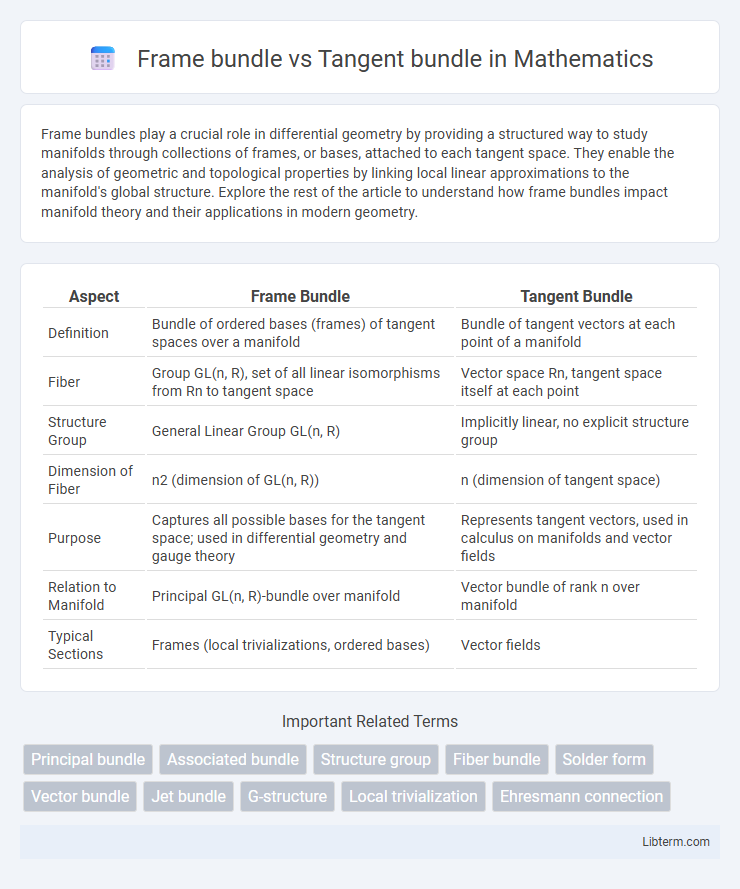
| Aspect | Frame Bundle | Tangent Bundle |
|---|---|---|
| Definition | Bundle of ordered bases (frames) of tangent spaces over a manifold | Bundle of tangent vectors at each point of a manifold |
| Fiber | Group GL(n, R), set of all linear isomorphisms from Rn to tangent space | Vector space Rn, tangent space itself at each point |
| Structure Group | General Linear Group GL(n, R) | Implicitly linear, no explicit structure group |
| Dimension of Fiber | n2 (dimension of GL(n, R)) | n (dimension of tangent space) |
| Purpose | Captures all possible bases for the tangent space; used in differential geometry and gauge theory | Represents tangent vectors, used in calculus on manifolds and vector fields |
| Relation to Manifold | Principal GL(n, R)-bundle over manifold | Vector bundle of rank n over manifold |
| Typical Sections | Frames (local trivializations, ordered bases) | Vector fields |
Introduction to Fiber Bundles in Differential Geometry
The tangent bundle is a fundamental example of a fiber bundle in differential geometry, associating each point on a smooth manifold with its tangent space. The frame bundle extends this concept by attaching an ordered basis (frame) of the tangent space to each point, forming a principal GL(n, R)-bundle that encodes linear isomorphisms of tangent spaces. Both bundles enable the study of manifold structures through local trivializations and transition functions, with the frame bundle providing a richer geometric framework for analyzing connections and curvature.
Defining the Tangent Bundle
The tangent bundle of a smooth manifold \(M\) is a vector bundle whose fibers consist of all tangent vectors at each point in \(M\), formally defined as the union \(\bigcup_{p \in M} T_pM\). Each fiber \(T_pM\) is a tangent space, capturing directional derivatives at point \(p\), and the bundle naturally inherits a manifold structure of twice the dimension of \(M\). The frame bundle, in contrast, associates to each point an ordered basis (frame) of the tangent space, forming a principal \(GL(n, \mathbb{R})\)-bundle, emphasizing the linear isomorphism group of the tangent spaces rather than the tangent vectors themselves.
Defining the Frame Bundle
The frame bundle of a smooth manifold is a principal GL(n, R)-bundle whose fiber at each point consists of all ordered bases (frames) of the tangent space at that point, providing a global way to encode linear isomorphisms of tangent spaces. Unlike the tangent bundle, which pairs each point with its tangent space itself, the frame bundle captures the entire set of linear frames, enabling the study of geometric structures such as connections and metrics via principal bundle theory. This construction plays a crucial role in differential geometry by linking abstract fiber bundles to concrete linear algebraic data on manifolds.
Structural Differences: Frame Bundle vs Tangent Bundle
The tangent bundle of a smooth manifold consists of all tangent spaces at every point, forming a vector bundle with fibers isomorphic to Euclidean space R^n. In contrast, the frame bundle is a principal GL(n, R)-bundle whose fibers comprise all ordered bases (frames) of the tangent spaces, capturing linear isomorphisms rather than individual vectors. Structurally, the tangent bundle encodes directional information as vectors, while the frame bundle encodes the linear structure of tangent spaces through collections of frames enabling the study of manifold geometry via group actions.
Transition Functions and Local Trivializations
The tangent bundle of a smooth manifold is locally trivialized by coordinate charts whose transition functions are given by the Jacobian matrices of the coordinate changes, representing linear transformations on tangent spaces. In contrast, the frame bundle, consisting of ordered bases of tangent spaces, has transition functions valued in the general linear group GL(n, R), reflecting changes of frames via invertible linear maps. Local trivializations of the frame bundle correspond to choosing smooth local sections that assign a basis to each tangent space, while those of the tangent bundle assign tangent vectors, making the frame bundle a principal GL(n, R)-bundle and the tangent bundle an associated vector bundle.
Role in Connections and Parallel Transport
Frame bundles provide a principal bundle structure essential for defining connections as Lie algebra-valued 1-forms, enabling a global framework for parallel transport through the action of the structure group GL(n). Tangent bundles, being vector bundles, utilize induced connections derived from frame bundle connections to define covariant derivatives and parallel transport along curves in the manifold. The frame bundle thus governs the geometric structure and holonomy, while the tangent bundle realizes this structure concretely on vector fields and tensors.
Applications in Geometry and Physics
The frame bundle, as a principal GL(n)-bundle, provides a structured way to study vector fields and frames on manifolds, essential in differential geometry and gauge theories in physics. The tangent bundle, comprising all tangent vectors, serves as the foundational construct for defining derivatives, vector fields, and dynamics on manifolds, integral to general relativity and classical mechanics. Applications in geometry use the frame bundle to analyze curvature and connections, while physics employs tangent bundles to model phase space and velocity fields.
Principal Bundle Structure of the Frame Bundle
The frame bundle of a smooth n-dimensional manifold M is a principal GL(n, R)-bundle whose fibers consist of ordered bases (frames) of the tangent spaces, providing a natural principal bundle structure that encodes linear isomorphisms of tangent spaces. In contrast, the tangent bundle TM is a vector bundle whose fibers are tangent spaces themselves, lacking the inherent principal bundle framework that the frame bundle possesses. The principal bundle structure of the frame bundle allows the application of connections and gauge theory methods, facilitating a more geometric and coordinate-independent approach to manifold analysis.
Reduction of Structure Group: Tangent vs Frame Bundle
The tangent bundle of a smooth manifold has the general linear group GL(n, R) as its structure group, while the frame bundle serves as a principal GL(n, R)-bundle providing a natural setting for reducing the structure group. Reduction of the structure group from GL(n, R) to a subgroup such as the orthogonal group O(n) corresponds to additional geometric structures, like Riemannian metrics, being imposed on the tangent bundle. The frame bundle encodes these reductions explicitly as subbundles, allowing a geometric interpretation of holonomy and connections related to coframe fields.
Summary: Choosing Between Frame and Tangent Bundles
The frame bundle provides a richer geometric structure by incorporating linear frames at each point, facilitating the study of connections and holonomy, while the tangent bundle focuses solely on tangent vectors, serving as the primary tool for differential calculus on manifolds. Selection between the two depends on the level of geometric detail required; use the tangent bundle for vector field analysis and the frame bundle when handling principal bundles and gauge theories. For applications in Riemannian geometry and gauge theory, frame bundles are essential, whereas tangent bundles suffice for most classical differential geometry and vector bundle theory.
Frame bundle Infographic
 libterm.com
libterm.com