An algebraic basis is a set of vectors in a vector space that is both linearly independent and spans the entire space, allowing every vector to be expressed uniquely as a linear combination of these basis vectors. Understanding the algebraic basis is crucial for solving systems of linear equations, performing vector space transformations, and simplifying complex algebraic structures. Explore the full article to deepen your grasp of how an algebraic basis underpins fundamental concepts in linear algebra.
Table of Comparison
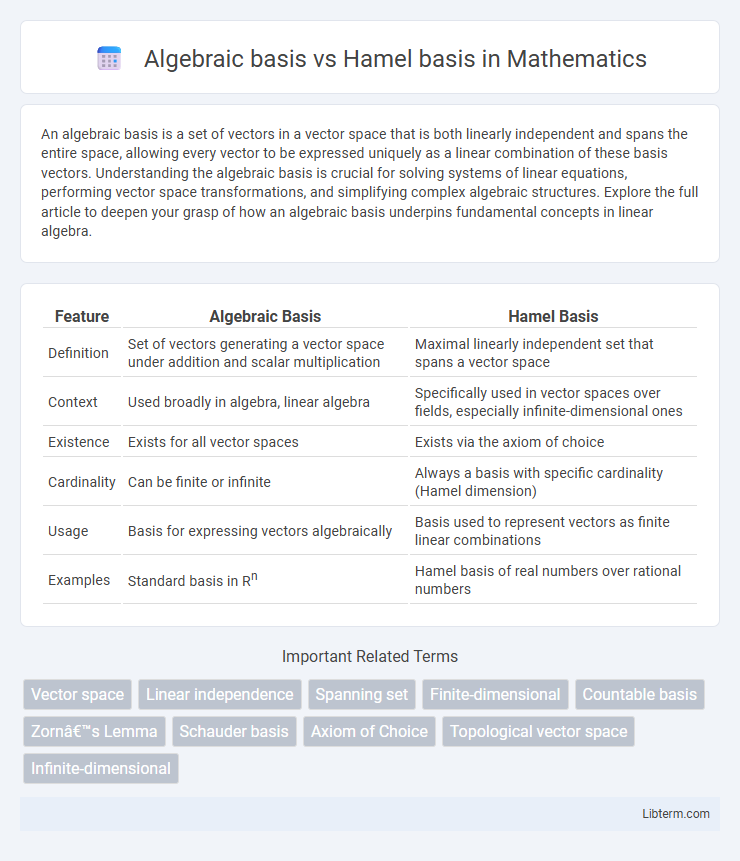
| Feature | Algebraic Basis | Hamel Basis |
|---|---|---|
| Definition | Set of vectors generating a vector space under addition and scalar multiplication | Maximal linearly independent set that spans a vector space |
| Context | Used broadly in algebra, linear algebra | Specifically used in vector spaces over fields, especially infinite-dimensional ones |
| Existence | Exists for all vector spaces | Exists via the axiom of choice |
| Cardinality | Can be finite or infinite | Always a basis with specific cardinality (Hamel dimension) |
| Usage | Basis for expressing vectors algebraically | Basis used to represent vectors as finite linear combinations |
| Examples | Standard basis in Rn | Hamel basis of real numbers over rational numbers |
Introduction to Vector Space Bases
A Hamel basis of a vector space is a set of vectors that are linearly independent and span the entire space, allowing every vector to be uniquely expressed as a finite linear combination of basis vectors. An algebraic basis refers specifically to such a Hamel basis in abstract algebra, where the vector space structure is defined over any field. Understanding these bases is fundamental in studying vector spaces since they provide the minimal building blocks for constructing all elements of the space.
Defining the Algebraic Basis
An algebraic basis, often called a Hamel basis, is a set of vectors in a vector space such that every element of the space can be uniquely expressed as a finite linear combination of these basis vectors. The defining property of an algebraic basis is that it spans the vector space and the vectors are linearly independent over the underlying field. Unlike other bases, the Hamel basis applies specifically to vector spaces without topological or metric constraints, emphasizing purely algebraic linear combinations.
Understanding the Hamel Basis
The Hamel basis, also known as an algebraic basis, is a set of vectors in a vector space such that every element in the space can be uniquely expressed as a finite linear combination of these vectors. Unlike infinite-dimensional spaces often associated with Hamel bases, an algebraic basis does not consider topological or norm-related properties, focusing purely on algebraic linear independence and span. Understanding the Hamel basis is crucial for grasping the structure of vector spaces abstractly, especially those without natural topological constraints.
Fundamental Differences Between Algebraic and Hamel Bases
An algebraic basis refers to a set of vectors in a vector space over a field such that every vector in the space can be expressed uniquely as a finite linear combination of these basis vectors, while a Hamel basis specifically denotes a basis for all vector spaces considered purely in terms of linear algebra without any topological constraints. The fundamental difference lies in the scope and context: every Hamel basis is an algebraic basis, but when topology is introduced (e.g., in infinite-dimensional normed spaces), the notion of a Schauder basis, which allows infinite linear combinations, becomes more relevant, contrasting with the finite support restriction of Hamel bases. Hamel bases often exist only from the axiom of choice and are typically non-constructive and huge in cardinality, whereas algebraic bases can sometimes be constructed explicitly in finite-dimensional settings.
Existence and Uniqueness in Infinite-Dimensional Spaces
Algebraic bases, also known as Hamel bases, exist for every vector space, including infinite-dimensional ones, by virtue of Zorn's Lemma, ensuring that every vector can be uniquely expressed as a finite linear combination of basis elements. However, in infinite-dimensional spaces, the uniqueness of representation is guaranteed only in the algebraic sense, as these bases are not necessarily compatible with any topological or normed structure, unlike Schauder bases that allow infinite series expansions. The existence of a Hamel basis is non-constructive and typically uncountable, making it impractical for explicit representation in functional analysis or Banach spaces, where topological considerations dominate.
Role of the Axiom of Choice in Basis Construction
The construction of a Hamel basis for any vector space fundamentally relies on the Axiom of Choice, enabling the selection of basis elements from infinite-dimensional spaces without explicit construction. Algebraic bases, in contrast, often refer to more explicitly defined generating sets within specific algebraic structures, where the Axiom of Choice may not be necessary. The crucial role of the Axiom of Choice ensures the existence of Hamel bases in all vector spaces, highlighting its importance in abstract linear algebra and functional analysis.
Practical Examples: Algebraic vs. Hamel Basis
An algebraic basis, often synonymous with a Hamel basis, is a set of vectors in a vector space such that every element can be uniquely expressed as a finite linear combination of these basis vectors. Practical examples include the standard basis in Euclidean spaces like R^n, where vectors are represented with coordinate tuples, illustrating a Hamel basis's role in finite-dimensional spaces. In contrast, infinite-dimensional vector spaces, such as function spaces, often highlight the complexity of finding a Hamel basis, as these bases are typically uncountably infinite and lack constructive methods, making them less practical for explicit computations compared to algebraic bases in finite dimensions.
Applications in Functional Analysis and Linear Algebra
An algebraic basis, also known as a Hamel basis, provides a minimal generating set for vector spaces enabling unique finite linear combinations, crucial in linear algebra for dimension theory and solving linear equations. In functional analysis, Hamel bases exist for infinite-dimensional spaces but are rarely used practically due to their non-constructive nature and lack of compatibility with topological structures. Instead, Schauder bases are preferred for applications involving convergence and continuity, while Hamel bases remain fundamental in theoretical proofs regarding vector space cardinality and linear independence.
Limitations and Challenges of Each Basis
Algebraic basis, or Hamel basis, faces limitations in infinite-dimensional vector spaces due to its non-constructive existence relying heavily on the axiom of choice, making explicit construction and computation impractical. Unlike orthonormal bases in Hilbert spaces, Hamel bases do not guarantee compatibility with topological or norm structures, which limits their applicability in functional analysis and complicates convergence considerations. Challenges also arise from the fact that infinite Hamel bases are uncountably large, leading to difficulties in handling them for practical problems in infinite-dimensional settings.
Summary and Comparative Insights
An algebraic basis, commonly known as a Hamel basis, is a set of vectors in a vector space such that every vector can be uniquely expressed as a finite linear combination of these basis elements. The Hamel basis emphasizes finite linear independence and spans, essential for understanding vector spaces over fields without relying on topological structure. Compared to other bases, such as Schauder bases in infinite-dimensional normed spaces, the Hamel basis is purely algebraic and often non-constructive, highlighting its foundational role in linear algebra and vector space theory.
Algebraic basis Infographic
 libterm.com
libterm.com