An affine hyperplane is a subspace in a vector space defined by a linear equation, representing a flat, infinite, and one dimension less than the ambient space. It plays a crucial role in geometry, optimization, and machine learning, serving as decision boundaries or solution sets. Explore the article to understand how affine hyperplanes shape mathematical models and applications for your work.
Table of Comparison
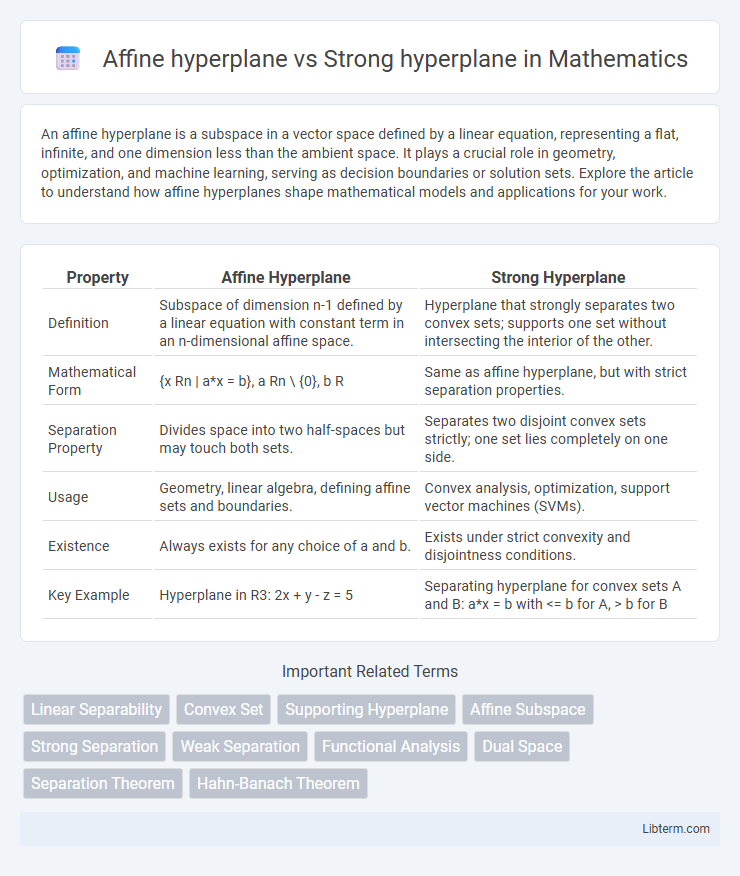
| Property | Affine Hyperplane | Strong Hyperplane |
|---|---|---|
| Definition | Subspace of dimension n-1 defined by a linear equation with constant term in an n-dimensional affine space. | Hyperplane that strongly separates two convex sets; supports one set without intersecting the interior of the other. |
| Mathematical Form | {x Rn | a*x = b}, a Rn \ {0}, b R | Same as affine hyperplane, but with strict separation properties. |
| Separation Property | Divides space into two half-spaces but may touch both sets. | Separates two disjoint convex sets strictly; one set lies completely on one side. |
| Usage | Geometry, linear algebra, defining affine sets and boundaries. | Convex analysis, optimization, support vector machines (SVMs). |
| Existence | Always exists for any choice of a and b. | Exists under strict convexity and disjointness conditions. |
| Key Example | Hyperplane in R3: 2x + y - z = 5 | Separating hyperplane for convex sets A and B: a*x = b with |
Introduction to Hyperplanes
An affine hyperplane in a vector space is a subspace of one dimension less that does not necessarily pass through the origin, defined by a linear equation offset by a constant term. A strong hyperplane, often referred to in optimization and machine learning contexts, represents a decision boundary with maximal margin separating different classes, emphasizing robustness in classification tasks. Understanding the distinction between affine and strong hyperplanes is essential for grasping geometric interpretations in linear algebra and the foundations of support vector machines.
Defining Affine Hyperplanes
An affine hyperplane is defined as a subspace of one dimension less than its ambient affine space, characterized by a linear equation of the form \( \mathbf{a} \cdot \mathbf{x} = b \), where \( \mathbf{a} \) is a non-zero vector and \( b \) is a scalar. Unlike strong hyperplanes, which are typically subspaces passing through the origin, affine hyperplanes can be translated away from the origin, representing shifted linear constraints. The distinction emphasizes that affine hyperplanes generalize linear subspaces by allowing affine translations, crucial in geometric modeling and optimization.
Understanding Strong Hyperplanes
Strong hyperplanes extend the concept of affine hyperplanes by incorporating additional structure such as orientation and norm constraints, playing a critical role in optimization and machine learning contexts like support vector machines. Unlike affine hyperplanes defined simply by linear equations and shifts, strong hyperplanes ensure maximal margin separability by enforcing strict inequalities and robust geometrical properties. Understanding strong hyperplanes involves recognizing their utility in achieving optimal classification boundaries and stability under perturbations in high-dimensional vector spaces.
Mathematical Formulation: Affine vs Strong
An affine hyperplane in \(\mathbb{R}^n\) is defined by the equation \( \mathbf{w}^\top \mathbf{x} + b = 0 \), where \(\mathbf{w} \in \mathbb{R}^n\) is the normal vector and \(b \in \mathbb{R}\) is the bias term, representing a flat subspace shifted by \(b\). A strong hyperplane extends the affine concept by incorporating margin constraints or additional robustness conditions, often expressed as inequalities like \( y_i(\mathbf{w}^\top \mathbf{x}_i + b) \geq \delta \) for a margin \(\delta > 0\) in classification contexts. This distinguishes strong hyperplanes in optimization problems such as Support Vector Machines, where the margin enforces separation strength beyond the simple affine formulation.
Key Properties and Differences
An affine hyperplane in n-dimensional space is defined as the set of points satisfying a linear equation of the form \( \mathbf{a} \cdot \mathbf{x} = b \), where \( \mathbf{a} \neq \mathbf{0} \) and \( b \) is a scalar, representing a translation of a linear hyperplane. Strong hyperplanes refer to hyperplanes associated with certain algebraic or topological constraints, often exhibiting stability or robustness properties in optimization or combinatorial geometry contexts. Key differences include that affine hyperplanes are characterized purely by linear algebraic conditions with translational degrees of freedom, while strong hyperplanes emphasize additional structural properties linked to the underlying mathematical framework or application domain.
Visual Representation and Geometric Intuition
An affine hyperplane in n-dimensional space is a flat subset defined by a linear equation with a constant term, representing a geometric boundary that does not necessarily pass through the origin, visually appearing as a shifted flat surface parallel to a linear hyperplane. A strong hyperplane, often synonymous with a linear hyperplane, always passes through the origin and can be expressed purely by homogeneous linear equations, making it visually a flat subspace that divides the space symmetrically into two halves. The key geometric intuition lies in the shift provided by the affine hyperplane, enabling translation of planar boundaries, while strong hyperplanes emphasize linear subspace properties critical in vector space analysis and classification tasks.
Applications in Machine Learning
Affine hyperplanes serve as decision boundaries in algorithms like support vector machines (SVMs) for classification tasks, where they separate data into distinct classes in high-dimensional feature spaces. Strong hyperplanes refer to hyperplanes with maximal margin properties, crucial in SVMs to enhance generalization by maximizing the distance between classes and the hyperplane, reducing overfitting. Applications extend to dimensionality reduction and neural network design, where the choice between affine and strong hyperplanes affects model robustness and interpretability in complex datasets.
Relevance in Optimization Problems
Affine hyperplanes define linear constraints of the form \( \mathbf{a}^\top \mathbf{x} = b \), playing a fundamental role in formulating feasible regions in linear optimization problems. Strong hyperplanes, often interpreted as supporting hyperplanes, are critical in convex optimization for separating feasible sets from infeasible ones, ensuring optimality conditions like the Karush-Kuhn-Tucker criteria. Understanding the geometric distinction between affine hyperplanes as exact solution boundaries and strong hyperplanes as optimality enforcers enhances the precision of constraint modeling and solution algorithms in optimization theory.
Comparative Advantages and Limitations
An affine hyperplane provides a linear decision boundary that allows translation, making it suitable for separating data that is not centered at the origin, while a strong hyperplane enforces stricter geometric constraints often improving robustness in classification tasks. Affine hyperplanes are computationally simpler and more flexible in adjusting to diverse datasets, but they may lack the discriminative power of strong hyperplanes under complex data distributions. Strong hyperplanes excel in scenarios requiring enhanced margin maximization and stability against noise, though they typically demand higher computational resources and more intricate optimization processes.
Conclusion and Future Perspectives
The distinction between affine hyperplanes, defined by linear equations with a translation vector, and strong hyperplanes characterized by stricter geometric constraints highlights their unique roles in data partitioning and geometric analysis. Future research may explore enhanced algorithms leveraging strong hyperplanes for improved classification accuracy in high-dimensional spaces and investigate affine hyperplanes' applications in optimization problems with affine constraints. Advancements in understanding the interplay between these hyperplane types could lead to breakthroughs in machine learning model interpretability and complex data structure analysis.
Affine hyperplane Infographic
 libterm.com
libterm.com