Symmetric designs balance elements equally on either side of a central axis, creating harmony and stability in visual compositions. This approach enhances readability and appeal by providing a predictable and organized structure. Explore the rest of the article to understand how symmetrical layouts can improve your design projects.
Table of Comparison
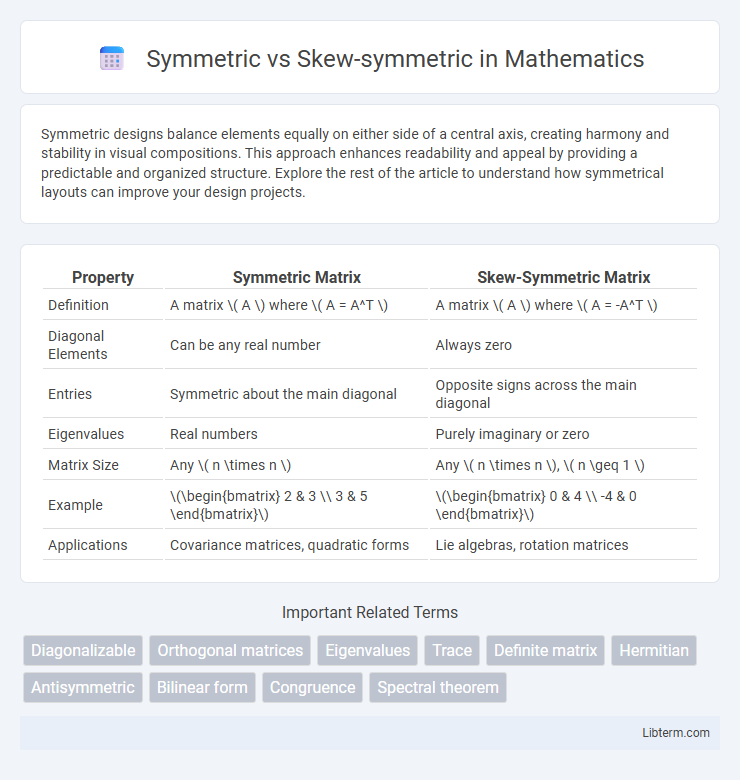
| Property | Symmetric Matrix | Skew-Symmetric Matrix |
|---|---|---|
| Definition | A matrix \( A \) where \( A = A^T \) | A matrix \( A \) where \( A = -A^T \) |
| Diagonal Elements | Can be any real number | Always zero |
| Entries | Symmetric about the main diagonal | Opposite signs across the main diagonal |
| Eigenvalues | Real numbers | Purely imaginary or zero |
| Matrix Size | Any \( n \times n \) | Any \( n \times n \), \( n \geq 1 \) |
| Example | \(\begin{bmatrix} 2 & 3 \\ 3 & 5 \end{bmatrix}\) | \(\begin{bmatrix} 0 & 4 \\ -4 & 0 \end{bmatrix}\) |
| Applications | Covariance matrices, quadratic forms | Lie algebras, rotation matrices |
Introduction to Matrices: Symmetric vs Skew-symmetric
Symmetric matrices are square matrices where the transpose equals the original matrix (A = AT), exhibiting mirror symmetry along the main diagonal. Skew-symmetric matrices satisfy the condition AT = -A, meaning all diagonal elements are zero and off-diagonal elements are negatives of their transposed counterparts. These matrix types play crucial roles in linear algebra, physics, and engineering, particularly in solving systems, eigenvalue problems, and representing certain transformations.
Defining Symmetric Matrices
Symmetric matrices are square matrices that satisfy the condition \( A = A^T \), where \( A^T \) is the transpose of matrix \( A \). Each element \( a_{ij} \) in position \((i,j)\) is equal to the element \( a_{ji} \) in position \((j,i)\), ensuring mirror symmetry across the main diagonal. This property is fundamental in various applications such as quadratic forms, eigenvalue problems, and optimization algorithms.
Characteristics of Skew-symmetric Matrices
Skew-symmetric matrices satisfy the property A^T = -A, meaning their transpose is equal to the negative of the original matrix. All diagonal elements of a skew-symmetric matrix are zero, which implies the trace of such matrices is always zero. These matrices have purely imaginary eigenvalues or zero and are commonly used in applications involving antisymmetric bilinear forms and rotation transformations in physics and engineering.
Mathematical Representations and Notations
A symmetric matrix \( A \) satisfies the condition \( A = A^T \), meaning its entries mirror across the main diagonal with \( a_{ij} = a_{ji} \) for all \( i, j \). In contrast, a skew-symmetric matrix \( B \) follows \( B = -B^T \), where the diagonal elements are zero and the off-diagonal elements satisfy \( b_{ij} = -b_{ji} \). Both types are fundamental in linear algebra, with symmetric matrices often associated with real eigenvalues and skew-symmetric matrices related to orthogonal transformations.
Key Properties of Symmetric Matrices
Symmetric matrices are square matrices equal to their own transpose, characterized by real eigenvalues and orthogonal eigenvectors, making them crucial in applications like quadratic forms and spectral theory. They exhibit positive semi-definiteness when all eigenvalues are non-negative, ensuring stability in optimization problems. Symmetric matrices contrast sharply with skew-symmetric matrices, which have zero diagonal elements and purely imaginary eigenvalues.
Distinctive Features of Skew-symmetric Matrices
Skew-symmetric matrices are characterized by the property that their transpose equals their negative, meaning \( A^T = -A \), which distinguishes them from symmetric matrices where \( A^T = A \). All diagonal elements of a skew-symmetric matrix are necessarily zero, as each diagonal element must satisfy \( a_{ii} = -a_{ii} \). These matrices have purely imaginary eigenvalues or zero, reflecting unique spectral properties crucial in physics and engineering applications.
Symmetric vs Skew-symmetric: Similarities and Differences
Symmetric and skew-symmetric matrices both belong to the class of square matrices and are defined based on their transpose properties: a symmetric matrix equals its transpose (A = AT), while a skew-symmetric matrix equals the negative of its transpose (A = -AT). Both types exhibit unique eigenvalue characteristics, where symmetric matrices have real eigenvalues and orthogonal eigenvectors, whereas skew-symmetric matrices have purely imaginary eigenvalues or zero. The key difference lies in their diagonal elements--symmetric matrices can have any real number on the diagonal, but skew-symmetric matrices must have zero diagonal entries.
Common Applications in Mathematics and Engineering
Symmetric matrices are widely used in engineering fields such as structural analysis and vibration studies due to their real eigenvalues and orthogonal eigenvectors, facilitating stability and mode shape calculations. Skew-symmetric matrices play a critical role in physics and robotics, especially in representing angular velocities and rotational dynamics through the use of Lie algebra and cross-product operations. Both matrix types support efficient computational algorithms, enhancing numerical solutions in finite element methods and control system designs.
Examples: Identifying Symmetric and Skew-symmetric Matrices
A symmetric matrix satisfies the condition A = A^T, meaning it is equal to its transpose, such as the matrix [[2, 3], [3, 5]], where the elements are mirrored across the main diagonal. In contrast, a skew-symmetric matrix satisfies A = -A^T, with an example being [[0, 4], [-4, 0]], where the transpose is the negative of the original matrix and diagonal elements are zero. Identifying symmetric matrices involves checking for equal elements across the diagonal, while skew-symmetric matrices have zeros on the diagonal and opposite signs in corresponding off-diagonal positions.
Conclusion: Choosing Between Symmetric and Skew-symmetric Matrices
Choosing between symmetric and skew-symmetric matrices depends on the problem context and properties needed; symmetric matrices are ideal for representing real-valued quadratic forms and ensure real eigenvalues. Skew-symmetric matrices, characterized by zero diagonal elements and purely imaginary eigenvalues, are essential in modeling rotational dynamics and antisymmetric relationships. Applications in physics, engineering, and computer science guide the selection based on whether symmetry or antisymmetry best captures the system's intrinsic structure.
Symmetric Infographic
 libterm.com
libterm.com