Path algebra provides a powerful framework for analyzing and modeling networks by representing paths as algebraic expressions. It enables you to efficiently compute properties such as connectivity, shortest paths, and flow capacity in complex graph structures. Explore the article to discover how path algebra can enhance your understanding of network dynamics and optimization.
Table of Comparison
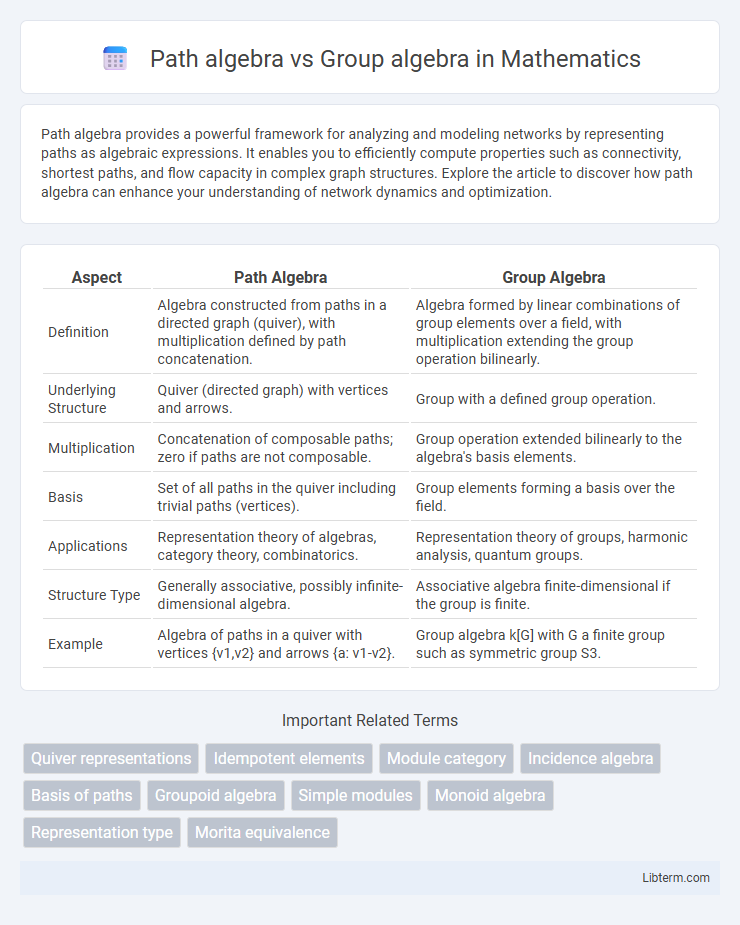
| Aspect | Path Algebra | Group Algebra |
|---|---|---|
| Definition | Algebra constructed from paths in a directed graph (quiver), with multiplication defined by path concatenation. | Algebra formed by linear combinations of group elements over a field, with multiplication extending the group operation bilinearly. |
| Underlying Structure | Quiver (directed graph) with vertices and arrows. | Group with a defined group operation. |
| Multiplication | Concatenation of composable paths; zero if paths are not composable. | Group operation extended bilinearly to the algebra's basis elements. |
| Basis | Set of all paths in the quiver including trivial paths (vertices). | Group elements forming a basis over the field. |
| Applications | Representation theory of algebras, category theory, combinatorics. | Representation theory of groups, harmonic analysis, quantum groups. |
| Structure Type | Generally associative, possibly infinite-dimensional algebra. | Associative algebra finite-dimensional if the group is finite. |
| Example | Algebra of paths in a quiver with vertices {v1,v2} and arrows {a: v1-v2}. | Group algebra k[G] with G a finite group such as symmetric group S3. |
Introduction to Path Algebras and Group Algebras
Path algebras are algebraic structures constructed from directed graphs where elements represent paths and multiplication corresponds to path concatenation, playing a crucial role in representation theory and combinatorics. Group algebras combine a group with a field, forming a vector space with a basis given by group elements, thereby enabling the study of group representations via linear algebra. Both algebras serve as fundamental frameworks bridging algebraic operations and combinatorial or group-theoretic structures.
Definitions and Key Concepts
Path algebra is an algebra constructed from all possible paths in a directed graph, with multiplication defined by path concatenation where composable, and zero otherwise. Group algebra forms an algebra by extending a group's elements into a vector space over a field, with multiplication derived from the group operation linearly extended across the space. Key concepts in path algebra include quivers and idempotent elements representing vertices, while group algebra centers on group elements and their representations as matrices or linear transformations.
Structural Differences Between Path and Group Algebras
Path algebras are constructed from directed graphs where elements are formal linear combinations of paths, capturing combinatorial structure through concatenation of paths as multiplication. Group algebras, formed by groups over a field, involve elements as formal sums of group elements with multiplication inherited from group operation, emphasizing symmetry and invertibility. Structurally, path algebras often have idempotent elements associated with vertices and are typically non-commutative with a basis of paths, while group algebras possess a basis indexed by group elements and may be commutative depending on the group's nature.
Basis Elements and Construction
Path algebra is constructed from the set of all finite paths in a directed graph, where basis elements correspond to individual paths including vertices treated as trivial paths. Group algebra is formed from a group G over a field, with basis elements indexed by the group elements themselves, and multiplication defined by the group operation extended linearly. While path algebra bases arise from sequences of composable arrows, group algebra bases derive directly from group elements, reflecting distinct algebraic structures encoded in their construction.
Representation Theory: Path vs Group Algebras
Path algebras and group algebras serve as fundamental structures in representation theory distinguished by their compositional elements and applications. Path algebras, constructed from quivers, represent directed graphs allowing for the study of modules via paths corresponding to basis elements, facilitating in-depth analysis of representations through linear maps between vector spaces over vertices. Conversely, group algebras encode group elements into algebraic structures, enabling representation theory to explore group actions by examining modules over these algebras, with irreducible representations linked to simple modules categorizing symmetry and group behavior.
Algebraic Properties and Operations
Path algebra emphasizes concatenation of paths as its primary operation, relying on directed graph structures where elements represent sequences of edges, allowing for idempotent elements corresponding to vertices. Group algebra involves combining group elements with coefficients from a field, respecting the group multiplication extended linearly, which ensures associativity and the presence of inverses corresponding to group elements. Both algebras are associative, but path algebras lack inherent invertibility for arbitrary paths, while group algebras inherit invertibility from the underlying group structure and support convolution-like multiplication operations.
Applications in Mathematics and Physics
Path algebra plays a crucial role in representation theory and category theory, modeling quivers and directed graphs to study their module categories and algebraic structures. Group algebra is fundamental in abstract algebra and harmonic analysis, enabling the representation of groups as algebraic objects to analyze symmetries and perform Fourier transforms. In physics, path algebra is applied in quantum mechanics and statistical mechanics to describe state transitions and particle interactions, while group algebra underpins quantum field theory and crystallography by facilitating the study of symmetry operations and conservation laws.
Examples of Path Algebras and Group Algebras
Path algebras arise from quivers, with each path in the quiver corresponding to a basis element; for example, the path algebra of a directed graph with vertices and arrows forms a vector space whose multiplication is given by path concatenation. Group algebras are constructed from groups by forming linear combinations of group elements over a field, such as the group algebra of the cyclic group \( C_n \), where each group element corresponds to a basis vector and multiplication extends linearly the group operation. Both algebras serve different structural purposes: path algebras model representations of quivers in representation theory, while group algebras encode group actions and provide a foundation for studying modules over groups.
Advantages and Limitations of Each Algebra
Path algebra excels in representing combinatorial structures and directed graphs, making it ideal for modeling paths and transitions in networks, but its complexity grows rapidly with graph size, limiting practical computation. Group algebra offers powerful tools for capturing symmetry and group actions in algebraic structures, facilitating representation theory and harmonic analysis, although it requires a well-defined group and may struggle with non-group-based relational data. Both algebras provide distinct frameworks: path algebra suits graph-theoretic problems, while group algebra is better for structural and symmetry analysis, each facing challenges related to scalability and domain applicability.
Summary and Future Directions
Path algebra and group algebra both serve as foundational tools in algebraic structures, where path algebra encodes combinatorial data of directed graphs through linear combinations of paths, while group algebra represents group elements with coefficients in a field, facilitating the study of group representations. Current research explores extending path algebra frameworks to higher-dimensional categories and modeling dynamic processes, whereas group algebra studies emphasize applications in quantum groups and noncommutative geometry. Future directions involve integrating path algebra methods with homological algebra techniques to analyze complex networks and leveraging group algebra in advancing cryptographic protocols and topological data analysis.
Path algebra Infographic
 libterm.com
libterm.com