A paracompact space is a topological space where every open cover has an open locally finite refinement, ensuring a more manageable and structured covering. This property generalizes compactness and plays a crucial role in analysis and geometry, especially in the study of manifolds and metric spaces. Explore the rest of the article to understand how paracompactness influences various mathematical theories and applications.
Table of Comparison
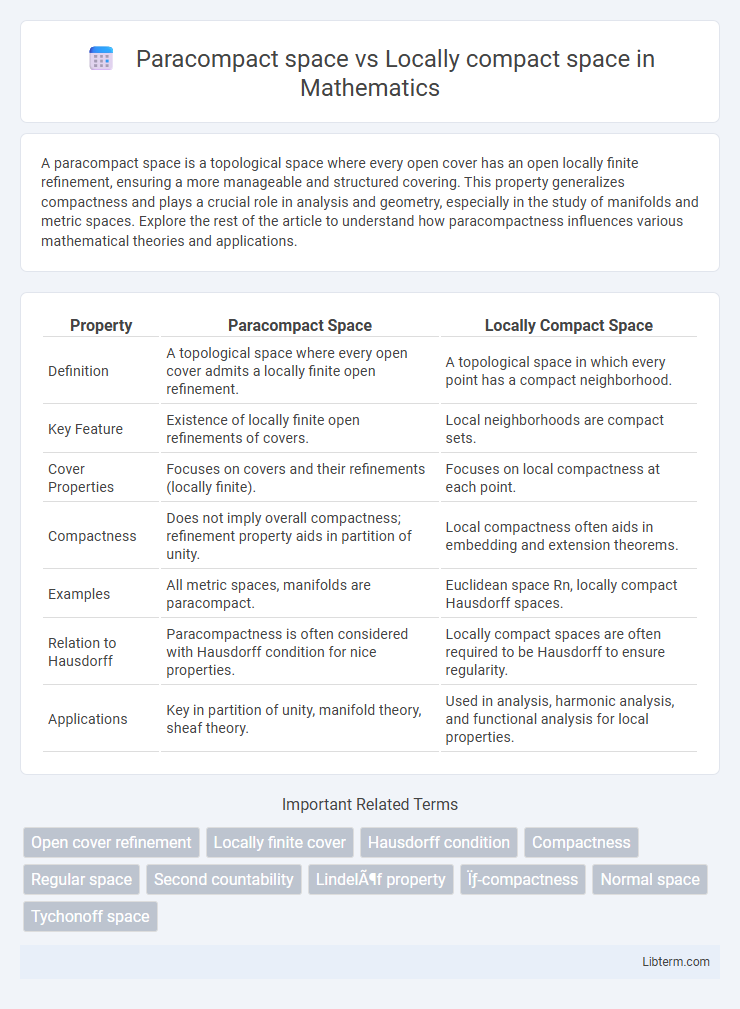
| Property | Paracompact Space | Locally Compact Space |
|---|---|---|
| Definition | A topological space where every open cover admits a locally finite open refinement. | A topological space in which every point has a compact neighborhood. |
| Key Feature | Existence of locally finite open refinements of covers. | Local neighborhoods are compact sets. |
| Cover Properties | Focuses on covers and their refinements (locally finite). | Focuses on local compactness at each point. |
| Compactness | Does not imply overall compactness; refinement property aids in partition of unity. | Local compactness often aids in embedding and extension theorems. |
| Examples | All metric spaces, manifolds are paracompact. | Euclidean space Rn, locally compact Hausdorff spaces. |
| Relation to Hausdorff | Paracompactness is often considered with Hausdorff condition for nice properties. | Locally compact spaces are often required to be Hausdorff to ensure regularity. |
| Applications | Key in partition of unity, manifold theory, sheaf theory. | Used in analysis, harmonic analysis, and functional analysis for local properties. |
Introduction to Topological Spaces
Paracompact spaces generalize compactness by ensuring every open cover has a locally finite open refinement, crucial for studying partitions of unity in topological analysis. Locally compact spaces require every point to have a compact neighborhood, enabling the extension of local properties to global contexts and supporting the construction of one-point compactifications. Both concepts are fundamental in the theory of topological spaces, influencing continuity, convergence, and manifold theory applications.
Defining Paracompact Spaces
Paracompact spaces are topological spaces in which every open cover has an open locally finite refinement, ensuring refined control over the topology's structure. Unlike locally compact spaces, which require each point to have a compact neighborhood, paracompactness emphasizes the existence of well-behaved open covers enabling partitions of unity. This property is fundamental in differential geometry and manifold theory, where paracompactness guarantees the extension of local constructions to global settings.
Defining Locally Compact Spaces
Locally compact spaces are topological spaces in which every point has a neighborhood whose closure is compact, highlighting a balance between local compactness and global topological structure. This property ensures that each point lies within a compactly contained neighborhood, facilitating the analysis of continuous functions and measures. While paracompact spaces require every open cover to have a locally finite open refinement, locally compact spaces emphasize the existence of compact neighborhoods, crucial in harmonic analysis and manifold theory.
Key Differences Between Paracompact and Locally Compact Spaces
Paracompact spaces generalize compactness by ensuring every open cover has a locally finite open refinement, whereas locally compact spaces require every point to have a compact neighborhood. Paracompactness emphasizes refinement properties of open covers, often guaranteeing partitions of unity, while local compactness focuses on the existence of compact neighborhoods around each point, which supports techniques in analysis and topology. Unlike locally compact spaces, paracompact spaces need not have compact neighborhoods but excel in handling cover refinements and are crucial in differential geometry and manifold theory.
Properties of Paracompact Spaces
Paracompact spaces generalize compactness by ensuring every open cover has a locally finite open refinement, which guarantees the existence of partitions of unity subordinate to any open cover, facilitating advanced analysis on manifolds. Unlike locally compact spaces that emphasize local compact neighborhoods, paracompactness ensures stronger global covering properties that simplify the handling of topological and geometric problems. This property is crucial in differential geometry and algebraic topology, where paracompactness supports the construction of Riemannian metrics and the application of sheaf theory.
Properties of Locally Compact Spaces
Locally compact spaces possess the key property that every point has a neighborhood base consisting of compact sets, enabling effective local analysis with compactness techniques. Such spaces are necessarily Hausdorff if they are also paracompact, ensuring desirable separation properties and facilitating the extension of continuous functions. Unlike paracompact spaces, which guarantee locally finite open refinements of any open cover, locally compact spaces emphasize the compactness of neighborhoods, making them crucial in measures, integration, and harmonic analysis.
Examples of Paracompact Spaces
Paracompact spaces include all metric spaces, such as Euclidean spaces \( \mathbb{R}^n \), which are both paracompact and locally compact. Another example is any Hausdorff space that is second-countable and regular, guaranteeing paracompactness without necessarily being locally compact, like certain infinite-dimensional Hilbert spaces. Conversely, locally compact spaces often feature compact neighborhoods around each point, but this property alone does not ensure paracompactness, illustrating the distinction through examples such as the long line in topology.
Examples of Locally Compact Spaces
Locally compact spaces include important examples such as Euclidean spaces \(\mathbb{R}^n\), where every point has a compact neighborhood like a closed ball, and discrete spaces, which are trivially locally compact since every singleton set is compact. Manifolds, including open subsets of Euclidean spaces, often serve as locally compact spaces due to their locally Euclidean structure. In contrast, paracompact spaces encompass all locally compact Hausdorff spaces but extend beyond them, including spaces that may not have local compactness yet admit locally finite open refinements.
Intersections and Relationships Between Paracompactness and Local Compactness
Paracompact spaces generalize compactness by requiring every open cover to have a locally finite open refinement, while locally compact spaces demand every point to have a compact neighborhood. The intersection of these properties emerges strongly in Hausdorff spaces, where every locally compact Hausdorff space is paracompact, linking local compactness to the global covering behavior of paracompactness. This relationship is fundamental in analysis and topology, as it ensures the existence of partitions of unity subordinate to open covers, facilitating advanced constructions and proofs.
Applications and Significance in Topology
Paracompact spaces, characterized by every open cover having a locally finite open refinement, play a crucial role in topology due to their ability to support partitions of unity, enabling advanced techniques in manifold theory and differential topology. Locally compact spaces, with every point having a compact neighborhood, are significant in harmonic analysis, potential theory, and the study of locally compact groups fundamental to abstract harmonic analysis and representation theory. The intersection of these properties supports the analysis of topological groups, sheaf theory, and the development of various cohomology theories, underscoring their broad applicability in modern mathematical research.
Paracompact space Infographic
 libterm.com
libterm.com