Decidable problems are those for which an algorithm can determine a definitive yes or no answer within a finite amount of time, making them fundamental in computational theory. Understanding decidability helps you grasp which questions computers can solve reliably and which remain beyond algorithmic reach. Explore the rest of the article to uncover how decidability impacts computer science and everyday problem-solving.
Table of Comparison
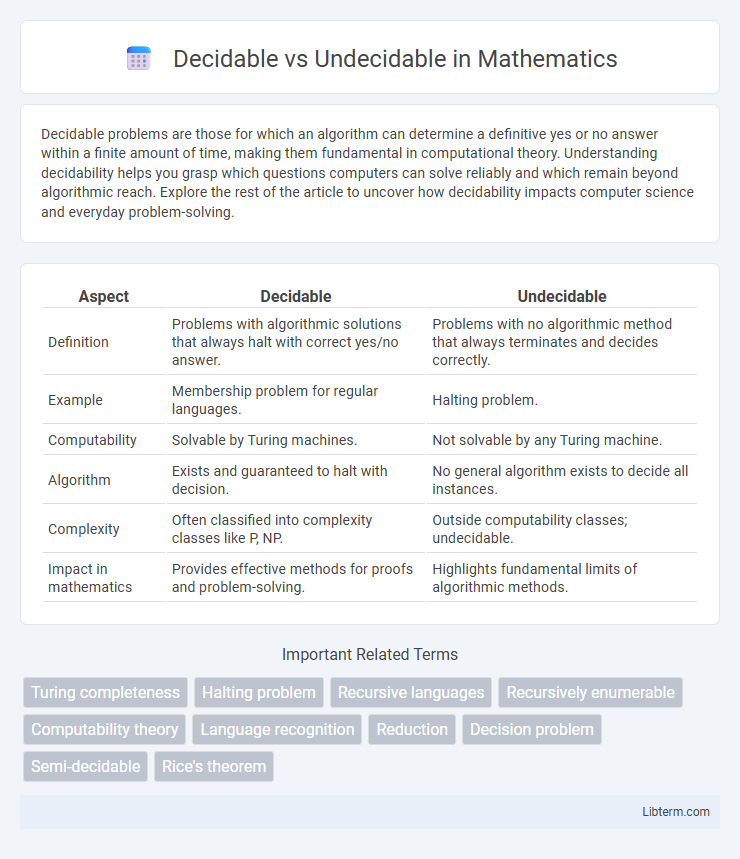
| Aspect | Decidable | Undecidable |
|---|---|---|
| Definition | Problems with algorithmic solutions that always halt with correct yes/no answer. | Problems with no algorithmic method that always terminates and decides correctly. |
| Example | Membership problem for regular languages. | Halting problem. |
| Computability | Solvable by Turing machines. | Not solvable by any Turing machine. |
| Algorithm | Exists and guaranteed to halt with decision. | No general algorithm exists to decide all instances. |
| Complexity | Often classified into complexity classes like P, NP. | Outside computability classes; undecidable. |
| Impact in mathematics | Provides effective methods for proofs and problem-solving. | Highlights fundamental limits of algorithmic methods. |
Introduction to Decidability
Decidability in computational theory refers to the ability of an algorithm to determine, in finite time, whether a given problem has a solution. Decidable problems have well-defined algorithms that always halt with a yes or no answer, whereas undecidable problems lack such algorithms and cannot be conclusively solved by any Turing machine. Understanding decidability is fundamental to distinguishing between problems solvable by computers and those inherently beyond algorithmic resolution.
What Are Decidable Problems?
Decidable problems are computational problems for which an algorithm can determine the correct yes-or-no answer for every input instance within a finite amount of time. These problems belong to the class of decision problems solvable by a Turing machine that halts on all inputs, ensuring that the solution is both correct and computable. Examples include determining whether a given number is prime or if a string belongs to a regular language, highlighting the clear boundary between solvable and unsolvable computational tasks.
Understanding Undecidable Problems
Undecidable problems are computational questions for which no algorithm can determine an answer for all possible inputs, reflecting fundamental limits of computation identified by Alan Turing's halting problem. These problems arise in areas such as formal language theory, logic, and automata theory, where the decision tasks cannot be fully automated. Understanding undecidable problems is crucial for recognizing the boundaries between solvable and unsolvable tasks in computer science and for the development of approximation or heuristic methods.
Key Differences: Decidable vs Undecidable
Decidable problems are those for which an algorithm can determine a yes or no answer in a finite amount of time, ensuring computability and guaranteed termination. Undecidable problems, such as the Halting Problem, have no algorithmic solution that can consistently resolve every case, reflecting intrinsic computational limitations. The key difference lies in decidability's algorithmic solvability versus undecidability's fundamental algorithmic impossibility.
Examples of Decidable Problems
Decidable problems include determining whether a given number is prime, verifying if a string belongs to a regular language using finite automata, and checking the membership of a word in a context-free language through pushdown automata. These problems can be solved by algorithms that always halt with a yes or no answer, such as the primality test based on the AKS algorithm or parsing techniques like the CYK algorithm. Examples Contrast with undecidable problems like the Halting Problem or the Entscheidungsproblem, where no algorithm can guarantee a definitive decision for all inputs.
Examples of Undecidable Problems
The Halting Problem, which determines whether a program will eventually stop or run indefinitely, is a classic example of an undecidable problem proven by Alan Turing. Another prominent undecidable problem is the Entscheidungsproblem, concerning the impossibility of creating an algorithm that decides the truth of all mathematical statements within first-order logic. Post's Correspondence Problem, involving the matching of sequences from two lists, also exemplifies undecidability in computational theory.
Importance in Computability Theory
Decidable problems are fundamental in computability theory as they represent questions for which an algorithm can determine a definitive yes or no answer within finite time, ensuring practical solvability. Undecidable problems highlight the inherent limitations of computational models by demonstrating tasks that no algorithm can solve universally, emphasizing boundaries within algorithmic processes. Understanding the distinction between decidable and undecidable problems is crucial for developing efficient algorithms and recognizing the theoretical limits of computation.
Real-world Implications
Decidable problems have well-defined algorithms that always provide an answer, enabling reliable automation in software development, cryptography, and artificial intelligence. Undecidable problems, lacking such algorithms, pose fundamental limits on computation and necessitate heuristic or approximate methods in areas like program verification and automated reasoning. Recognizing these distinctions guides practical decision-making in technology design, resource allocation, and risk management within computational fields.
Common Misconceptions
Many mistakenly believe that all computational problems can be categorized as either easily solvable or unsolvable, but decidable problems have algorithms that always halt with a correct yes/no answer, while undecidable problems lack any algorithmic solution that guarantees halting for all inputs. Another common misconception is that undecidability implies practical impossibility; some undecidable problems can still be approached with heuristics or partial algorithms that work on specific cases. Understanding that decidability is a formal concept tied to Turing machine computations helps clarify why some problems defy algorithmic resolution despite appearing intuitively solvable.
Conclusion: Navigating Decidability
Decidable problems have algorithms that guarantee a solution within finite time, enabling reliable automation and verification in computer science. Undecidable problems lack such algorithms, highlighting fundamental limits in computation and necessitating approximation or heuristic methods. Understanding the boundary between decidability and undecidability is crucial for designing efficient algorithms and recognizing when problem-solving efforts may be inherently infeasible.
Decidable Infographic
 libterm.com
libterm.com