A subgroup is a smaller group within a larger group that shares certain characteristics or interests, creating a more focused community. Understanding how subgroups function can enhance your ability to analyze social dynamics and group behavior. Dive into the rest of the article to explore the important roles subgroups play in various contexts.
Table of Comparison
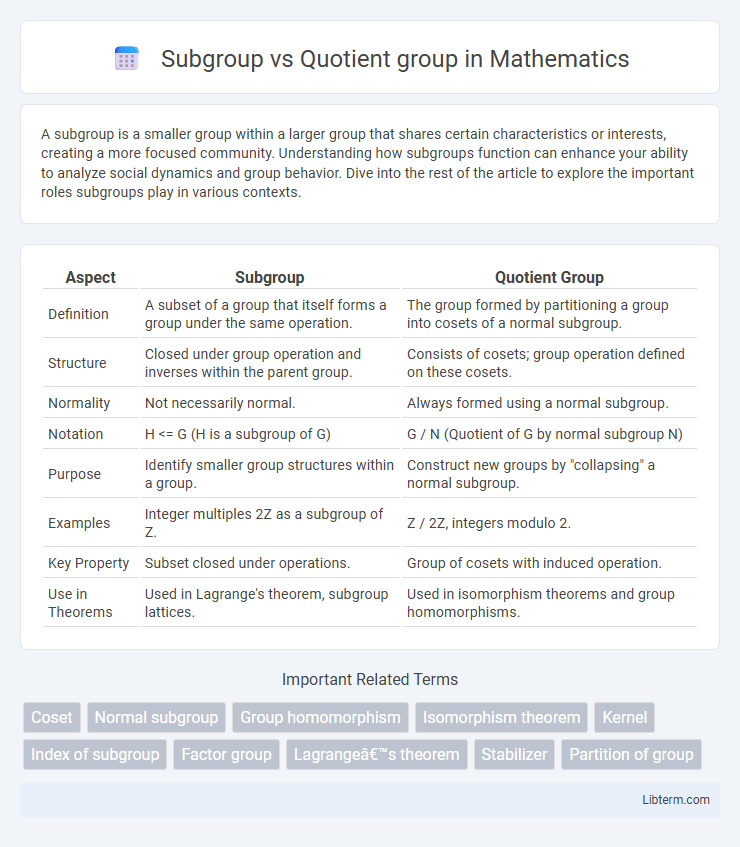
| Aspect | Subgroup | Quotient Group |
|---|---|---|
| Definition | A subset of a group that itself forms a group under the same operation. | The group formed by partitioning a group into cosets of a normal subgroup. |
| Structure | Closed under group operation and inverses within the parent group. | Consists of cosets; group operation defined on these cosets. |
| Normality | Not necessarily normal. | Always formed using a normal subgroup. |
| Notation | H <= G (H is a subgroup of G) | G / N (Quotient of G by normal subgroup N) |
| Purpose | Identify smaller group structures within a group. | Construct new groups by "collapsing" a normal subgroup. |
| Examples | Integer multiples 2Z as a subgroup of Z. | Z / 2Z, integers modulo 2. |
| Key Property | Subset closed under operations. | Group of cosets with induced operation. |
| Use in Theorems | Used in Lagrange's theorem, subgroup lattices. | Used in isomorphism theorems and group homomorphisms. |
Introduction to Subgroups and Quotient Groups
Subgroups are subsets of a group that themselves satisfy the group axioms, allowing the study of internal symmetries and structural properties within the original group. Quotient groups, formed by partitioning a group via a normal subgroup, provide a way to analyze group behavior through equivalence classes and factor structures. Understanding the role of normal subgroups is crucial for defining quotient groups and enables the simplification of complex group interactions into more manageable forms.
Definitions: Subgroup vs Quotient Group
A subgroup is a subset of a group that itself forms a group under the same operation, satisfying closure, associativity, identity, and invertibility. A quotient group, also called a factor group, is formed by partitioning a group into cosets of a normal subgroup, with group operation defined on these cosets. The key difference lies in structure: subgroups exist within the original group, while quotient groups result from collapsing a normal subgroup to the identity element.
Properties of Subgroups
Subgroups of a group G are subsets that themselves form groups under the operation of G, characterized by closure, existence of inverses, and containing the identity element. Every subgroup H of G satisfies the subgroup criteria: for all elements a, b in H, the product ab-1 is also in H, ensuring internal consistency of the group operation within H. Unlike quotient groups, which are formed by partitioning G into cosets of a normal subgroup, subgroups serve as foundational structures preserving the group's operation without forming new elements outside H.
Properties of Quotient Groups
Quotient groups, formed by partitioning a group G by a normal subgroup N, inherit a group structure where the operation is well-defined on cosets. Key properties of quotient groups include the fact that the natural projection map from G to G/N is a surjective homomorphism with kernel N, enabling the First Isomorphism Theorem. The quotient group reflects the structure of G modulo N, simplifying analysis by collapsing elements of N into the identity element of G/N.
Examples of Subgroups
Examples of subgroups include the set of even integers within the group of all integers under addition, and the group of rotations in the plane as a subgroup of the group of all isometries. Each subgroup must satisfy closure, contain the identity element, and include inverses of its elements. In contrast, quotient groups arise by partitioning a group into cosets of a normal subgroup, forming a new group structure on these cosets.
Examples of Quotient Groups
Quotient groups arise when a normal subgroup N of a group G is used to partition G into cosets, forming the group G/N with well-defined group operation. For example, the integers modulo n, denoted by Z/nZ, is a quotient group formed by taking the subgroup nZ of all integer multiples of n in the group of integers Z under addition. Another example is the quotient group of the symmetric group S_4 by its alternating subgroup A_4, which yields a group isomorphic to the cyclic group of order 2, reflecting the partition of even and odd permutations.
Key Differences Between Subgroups and Quotient Groups
Subgroups are subsets of a group that themselves satisfy the group axioms, serving as building blocks within the original group's structure. Quotient groups, formed by partitioning a group into cosets of a normal subgroup, represent the group's structure modulo that normal subgroup. The key difference lies in subgroups being subsets with inherited operations, while quotient groups arise from equivalence classes defined by normal subgroups, reflecting a group's factorization.
Importance in Group Theory
Subgroups provide insight into the internal structure of a group by identifying smaller groups that preserve the operation and satisfy closure, identity, and inverses, essential for understanding symmetry and invariants. Quotient groups, formed by partitioning a group into cosets using a normal subgroup, facilitate the study of group homomorphisms and allow classification of groups through factorization, crucial for simplifying complex group behavior. Both concepts play a pivotal role in analyzing group properties, enabling decomposition and reconstruction of groups in algebraic research and applications.
Applications of Subgroups and Quotient Groups
Subgroups play a crucial role in symmetry analysis and stabilizing structures within algebraic systems, enabling the classification of solutions in fields like crystallography and coding theory. Quotient groups facilitate simplification of complex group structures by partitioning them into cosets, providing powerful tools in topology and group homomorphism analysis. Both concepts are instrumental in understanding normal subgroups, factor groups, and their applications in cryptography and theoretical physics.
Conclusion: Understanding Subgroups and Quotient Groups
Understanding subgroups and quotient groups is essential for grasping the structure of groups in abstract algebra. A subgroup is a subset of a group that itself forms a group under the same operation, while a quotient group arises from partitioning a group by a normal subgroup, creating a new group of cosets. Mastery of these concepts enables deeper insights into group homomorphisms, group actions, and the classification of groups.
Subgroup Infographic
 libterm.com
libterm.com